Menu Close

1-let-f-x-0-dt-t-3-x-3-with-x-gt-0-calculate-f-x-2-find-also-g-x-0-dt-t-3-x-3-2-3-find-the-values-of-integrals-0-dt-t-3-1-and-0-dt-

Tinku Tara 0 Comments
Pin




Question Number 65288 by mathmax by abdo last updated on 27/Jul/19
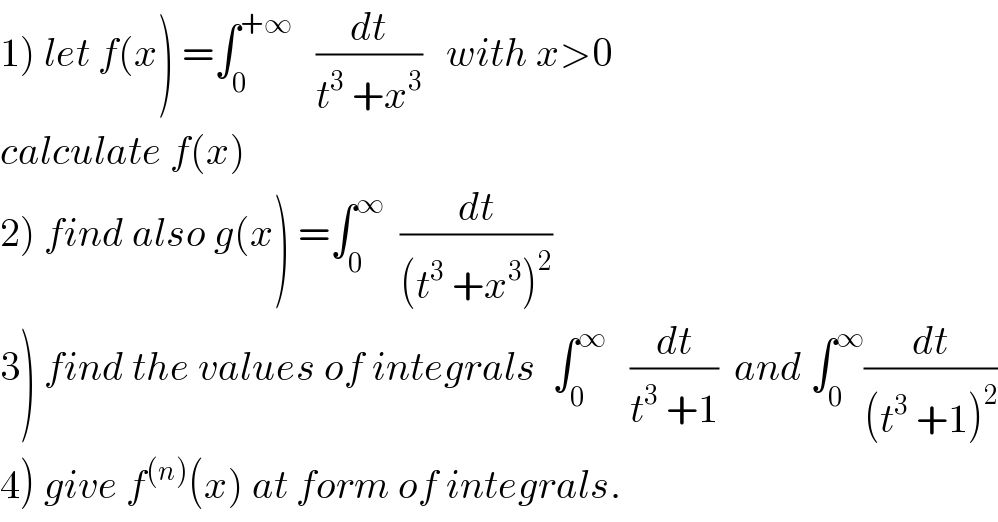
1) let f(x) =∫_0 ^(+∞) (dt/(t^3 +x^3 )) with x>0 calculate f(x) 2) find also g(x) =∫_0 ^∞ (dt/((t^3 +x^3 )^2 )) 3) find the values of integrals ∫_0 ^∞ (dt/(t^3 +1)) and ∫_0 ^∞ (dt/((t^3 +1)^2 )) 4) give f^((n)) (x) at form of integrals.
$$\left.\mathrm{1}\right)\:{let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+{x}^{\mathrm{3}} }\:\:\:{with}\:{x}>\mathrm{0} \\ $$$${calculate}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{also}\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\left({t}^{\mathrm{3}} \:+{x}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{values}\:{of}\:{integrals}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+\mathrm{1}}\:\:{and}\:\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left({t}^{\mathrm{3}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{4}\right)\:{give}\:{f}^{\left({n}\right)} \left({x}\right)\:{at}\:{form}\:{of}\:{integrals}. \\ $$
Commented by mathmax by abdo last updated on 30/Jul/19
1) f(x)=∫_0 ^∞ (dt/(t^3 +x^3 ))dt ⇒f(x) =∫_0 ^∞ (dt/((t+x)(t^2 −xt +x^2 ))) let decompose F(t) =(1/((t+x)(t^2 −xt +x^2 ))) F(t) =(a/(t+x)) +((bt +c)/(t^2 −xt +x^2 )) (x>0) a =lim_(t→−x) (t+x)F(t) =(1/(3x^2 )) lim_(t→+∞) tF(t) =0 =a+b ⇒b =−(1/(3x^2 )) ⇒F(t)=(1/(3x^2 (t+x))) +((−(1/(3x^2 ))t+c)/(t^2 −xt+x^2 )) F(0) =(1/x^3 ) =(1/(3x^3 )) +(c/x^2 ) ⇒c =0 ⇒1=(1/3) +xc ⇒xc =(2/3) ⇒c =(2/(3x)) ⇒ F(t) =(1/(3x^2 (t+x))) +((−(t/(3x^2 ))+(2/(3x)))/(t^2 −xt+x^2 )) =(1/(3x^2 (t+x)))−(1/(3x^2 )) ((t−2x)/(t^2 −xt +x^2 )) ⇒ f(x) =(1/(3x^2 )){ ∫_0 ^∞ (dt/(t+x)) −∫_0 ^∞ ((t−2x)/(t^2 −xt +x^2 ))} =(1/(3x^2 )){ ∫_0 ^∞ (dt/(t+x)) −(1/2)∫_0 ^∞ ((2t−x+x)/(t^2 −xt +x^2 )) +∫_0 ^∞ ((2x)/(t^2 −xt+x^2 ))dt} =(1/(3x^2 )){ [ln∣((t+x)/( (√(t^2 −xt+x^2 ))))∣]_0 ^(+∞) +((3x)/2)∫_0 ^∞ (dt/(t^2 −xt +x^2 ))} =(1/(2x))∫_0 ^∞ (dt/(t^2 −xt +x^2 )) and ∫_0 ^∞ (dt/(t^2 −xt +x^2 )) =∫_0 ^∞ (dt/(t^2 −2(x/2)t +(x^2 /4)+x^2 −(x^2 /4))) =∫_0 ^∞ (dt/((t−(x/2))^2 +(3/4)x^2 )) =_(t−(x/2)=((√3)/2)xu) ∫_(−(1/( (√3)))) ^(+∞) (1/((3/4)x^2 (1+u^2 )))((√3)/2) xdu =(4/(3x^2 )) ((√3)/2) x ∫_(−(1/( (√3)))) ^(+∞) (du/(1+u^2 )) =(2/(x(√3)))[arctan(u)]_(−(1/( (√3)))) ^(+∞) =(2/(x(√3))){(π/2) +arctan((1/( (√3))))} =(2/(x(√3))){π −arctan((√3)) =(2/(x(√3))){π−(π/3)} =(2/(x(√3)))((2π)/3) =((4π)/(3x(√3))) ⇒f(x)=(1/(2x)) ((4π)/(3x(√3))) =((2π)/(3x^2 (√3))) ⇒ f(x) =((2π)/(3(√3)x^2 )) (x>0)
$$\left.\mathrm{1}\right)\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+{x}^{\mathrm{3}} }{dt}\:\Rightarrow{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\left({t}+{x}\right)\left({t}^{\mathrm{2}} −{xt}\:+{x}^{\mathrm{2}} \right)} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)\:=\frac{\mathrm{1}}{\left({t}+{x}\right)\left({t}^{\mathrm{2}} −{xt}\:+{x}^{\mathrm{2}} \right)} \\ $$$${F}\left({t}\right)\:=\frac{{a}}{{t}+{x}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} −{xt}\:+{x}^{\mathrm{2}} }\:\:\:\:\:\left({x}>\mathrm{0}\right) \\ $$$${a}\:={lim}_{{t}\rightarrow−{x}} \left({t}+{x}\right){F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}\:=−\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} \left({t}+{x}\right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }{t}+{c}}{{t}^{\mathrm{2}} −{xt}+{x}^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{3}} }\:+\frac{{c}}{{x}^{\mathrm{2}} }\:\Rightarrow{c}\:=\mathrm{0}\:\Rightarrow\mathrm{1}=\frac{\mathrm{1}}{\mathrm{3}}\:+{xc}\:\Rightarrow{xc}\:=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow{c}\:=\frac{\mathrm{2}}{\mathrm{3}{x}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} \left({t}+{x}\right)}\:+\frac{−\frac{{t}}{\mathrm{3}{x}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}{x}}}{{t}^{\mathrm{2}} −{xt}+{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} \left({t}+{x}\right)}−\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }\:\frac{{t}−\mathrm{2}{x}}{{t}^{\mathrm{2}} −{xt}\:+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }\left\{\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}+{x}}\:−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}−\mathrm{2}{x}}{{t}^{\mathrm{2}} −{xt}\:+{x}^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }\left\{\:\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{{t}+{x}}\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{t}−{x}+{x}}{{t}^{\mathrm{2}} −{xt}\:+{x}^{\mathrm{2}} }\:\:+\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{x}}{{t}^{\mathrm{2}} −{xt}+{x}^{\mathrm{2}} }{dt}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }\left\{\:\:\left[{ln}\mid\frac{{t}+{x}}{\:\sqrt{{t}^{\mathrm{2}} −{xt}+{x}^{\mathrm{2}} }}\mid\right]_{\mathrm{0}} ^{+\infty} \:+\frac{\mathrm{3}{x}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{2}} −{xt}\:+{x}^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{x}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} −{xt}\:+{x}^{\mathrm{2}} }\:\:\:{and}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{2}} −{xt}\:+{x}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{2}\frac{{x}}{\mathrm{2}}{t}\:+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\left({t}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{2}} }\:=_{{t}−\frac{{x}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{xu}} \:\:\:\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\:\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{2}} \left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{xdu} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}{x}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{x}\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{{x}\sqrt{\mathrm{3}}}\left[{arctan}\left({u}\right)\right]_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \\ $$$$=\frac{\mathrm{2}}{{x}\sqrt{\mathrm{3}}}\left\{\frac{\pi}{\mathrm{2}}\:+{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right\}\:=\frac{\mathrm{2}}{{x}\sqrt{\mathrm{3}}}\left\{\pi\:−{arctan}\left(\sqrt{\mathrm{3}}\right)\:=\frac{\mathrm{2}}{{x}\sqrt{\mathrm{3}}}\left\{\pi−\frac{\pi}{\mathrm{3}}\right\}\right. \\ $$$$=\frac{\mathrm{2}}{{x}\sqrt{\mathrm{3}}}\frac{\mathrm{2}\pi}{\mathrm{3}}\:=\frac{\mathrm{4}\pi}{\mathrm{3}{x}\sqrt{\mathrm{3}}}\:\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}{x}}\:\frac{\mathrm{4}\pi}{\mathrm{3}{x}\sqrt{\mathrm{3}}}\:=\frac{\mathrm{2}\pi}{\mathrm{3}{x}^{\mathrm{2}} \sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\left({x}>\mathrm{0}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 30/Jul/19
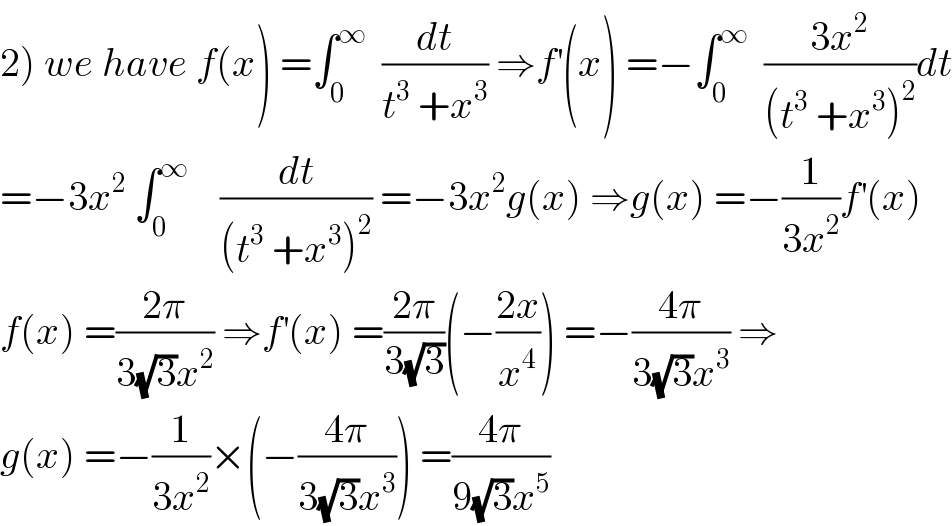
2) we have f(x) =∫_0 ^∞ (dt/(t^3 +x^3 )) ⇒f^′ (x) =−∫_0 ^∞ ((3x^2 )/((t^3 +x^3 )^2 ))dt =−3x^2 ∫_0 ^∞ (dt/((t^3 +x^3 )^2 )) =−3x^2 g(x) ⇒g(x) =−(1/(3x^2 ))f^′ (x) f(x) =((2π)/(3(√3)x^2 )) ⇒f^′ (x) =((2π)/(3(√3)))(−((2x)/x^4 )) =−((4π)/(3(√3)x^3 )) ⇒ g(x) =−(1/(3x^2 ))×(−((4π)/(3(√3)x^3 ))) =((4π)/(9(√3)x^5 ))
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+{x}^{\mathrm{3}} }\:\Rightarrow{f}^{'} \left({x}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{3}{x}^{\mathrm{2}} }{\left({t}^{\mathrm{3}} \:+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dt} \\ $$$$=−\mathrm{3}{x}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{\left({t}^{\mathrm{3}} \:+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }\:=−\mathrm{3}{x}^{\mathrm{2}} {g}\left({x}\right)\:\Rightarrow{g}\left({x}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }{f}^{'} \left({x}\right) \\ $$$${f}\left({x}\right)\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}{x}^{\mathrm{2}} }\:\Rightarrow{f}^{'} \left({x}\right)\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\left(−\frac{\mathrm{2}{x}}{{x}^{\mathrm{4}} }\right)\:=−\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}{x}^{\mathrm{3}} }\:\Rightarrow \\ $$$${g}\left({x}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }×\left(−\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}{x}^{\mathrm{3}} }\right)\:=\frac{\mathrm{4}\pi}{\mathrm{9}\sqrt{\mathrm{3}}{x}^{\mathrm{5}} } \\ $$
Commented by mathmax by abdo last updated on 30/Jul/19
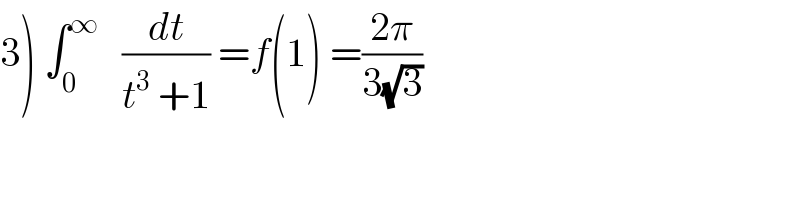
3) ∫_0 ^∞ (dt/(t^3 +1)) =f(1) =((2π)/(3(√3)))
$$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+\mathrm{1}}\:={f}\left(\mathrm{1}\right)\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 30/Jul/19
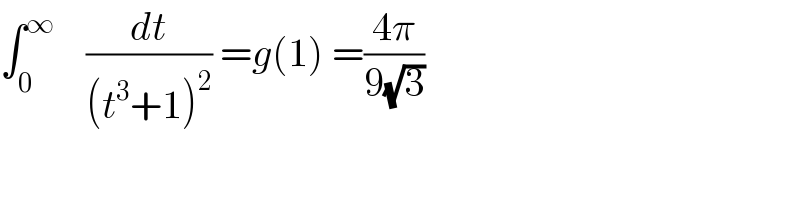
∫_0 ^∞ (dt/((t^3 +1)^2 )) =g(1) =((4π)/(9(√3)))
$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{\left({t}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }\:={g}\left(\mathrm{1}\right)\:=\frac{\mathrm{4}\pi}{\mathrm{9}\sqrt{\mathrm{3}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *