Question Number 123874 by john_santu last updated on 29/Nov/20
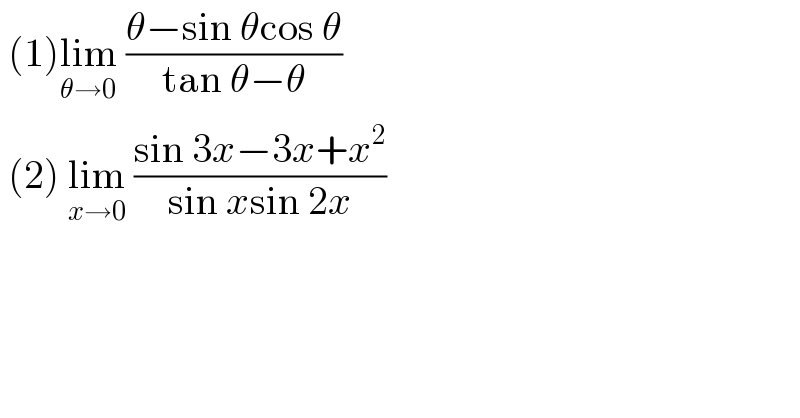
$$\:\left(\mathrm{1}\right)\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\theta−\mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{tan}\:\theta−\theta} \\ $$$$\:\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{3}{x}−\mathrm{3}{x}+{x}^{\mathrm{2}} }{\mathrm{sin}\:{x}\mathrm{sin}\:\mathrm{2}{x}} \\ $$
Answered by liberty last updated on 29/Nov/20
![solve this question (1) lim_(θ→0) ((θ−sin θcos θ)/(tan θ−θ)) (2) lim_(x→0) ((sin 3x−3x+x^2 )/(sin x sin 2x)) Solution : (1) by L′Hopital rule lim_(θ→0) ((θ−(1/2)sin 2θ)/(tan θ−θ)) = lim_(θ→0) ((1−cos 2θ)/(sec^2 θ−1)) lim_(θ→0) ((cos^2 θ(2sin^2 ((θ/2))))/(sin^2 θ)) = lim_(θ→0) 2(((sin (θ/2))/(tan θ)))^2 = (1/2) (2) lim_(x→0) ((sin 3x−3x+x^2 )/(−(1/2)(cos 3x−cos x))) = −2×lim_(x→0) ((3cos 3x−3+2x)/(−3sin 3x+sin x)) = −2×lim_(x→0) ((−9sin 3x+2)/(−9cos 3x+cos x)) = −2× [(2/(−8)) ] = (1/2).](https://www.tinkutara.com/question/Q123875.png)
$$\:{solve}\:{this}\:{question}\: \\ $$$$\left(\mathrm{1}\right)\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\theta−\mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{tan}\:\theta−\theta} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{3}{x}−\mathrm{3}{x}+{x}^{\mathrm{2}} }{\mathrm{sin}\:{x}\:\mathrm{sin}\:\mathrm{2}{x}} \\ $$$${Solution}\::\: \\ $$$$\left(\mathrm{1}\right)\:{by}\:{L}'{Hopital}\:{rule}\: \\ $$$$\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\theta−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{tan}\:\theta−\theta}\:=\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{sec}\:^{\mathrm{2}} \theta−\mathrm{1}} \\ $$$$\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:^{\mathrm{2}} \theta\left(\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\right)}{\mathrm{sin}\:^{\mathrm{2}} \theta}\:=\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{2}\left(\frac{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\mathrm{tan}\:\theta}\right)^{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{3}{x}−\mathrm{3}{x}+{x}^{\mathrm{2}} }{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:{x}\right)}\:= \\ $$$$\:\:−\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3cos}\:\mathrm{3}{x}−\mathrm{3}+\mathrm{2}{x}}{−\mathrm{3sin}\:\mathrm{3}{x}+\mathrm{sin}\:{x}}\:=\:−\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{9sin}\:\mathrm{3}{x}+\mathrm{2}}{−\mathrm{9cos}\:\mathrm{3}{x}+\mathrm{cos}\:{x}} \\ $$$$=\:−\mathrm{2}×\:\left[\frac{\mathrm{2}}{−\mathrm{8}}\:\right]\:=\:\frac{\mathrm{1}}{\mathrm{2}}. \\ $$
Answered by Dwaipayan Shikari last updated on 29/Nov/20
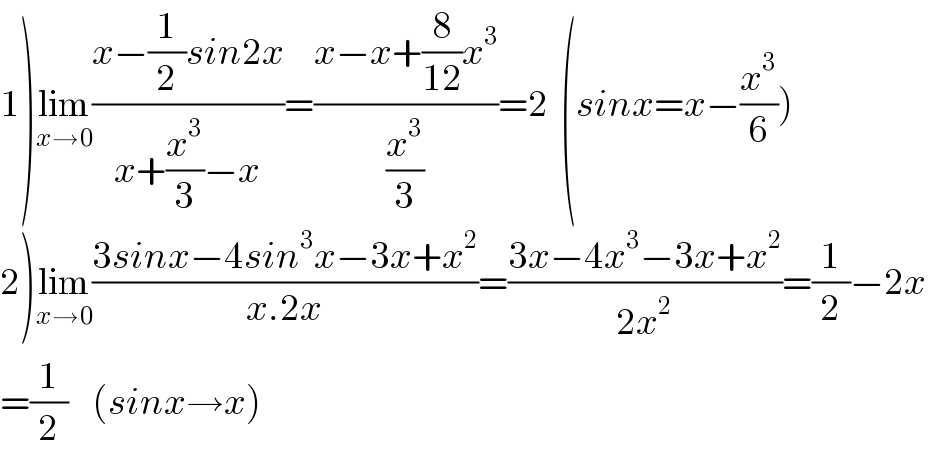
$$\left.\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{x}}{{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−{x}}=\frac{{x}−{x}+\frac{\mathrm{8}}{\mathrm{12}}{x}^{\mathrm{3}} }{\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}=\mathrm{2}\:\:\left({sinx}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right) \\ $$$$\left.\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{sinx}−\mathrm{4}{sin}^{\mathrm{3}} {x}−\mathrm{3}{x}+{x}^{\mathrm{2}} }{{x}.\mathrm{2}{x}}=\frac{\mathrm{3}{x}−\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x}+{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\left({sinx}\rightarrow{x}\right) \\ $$
