Menu Close

1-lim-x-0-1-cos-2x-x-2-2-cot-3-x-csc-3-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 121502 by bramlexs22 last updated on 08/Nov/20
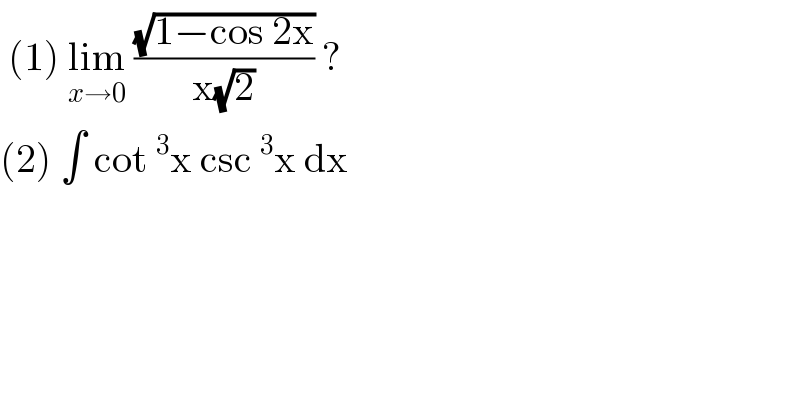
(1) lim_(x→0) ((√(1−cos 2x))/(x(√2))) ? (2) ∫ cot^3 x csc^3 x dx
$$\:\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{2x}}}{\mathrm{x}\sqrt{\mathrm{2}}}\:? \\ $$$$\left(\mathrm{2}\right)\:\int\:\mathrm{cot}\:^{\mathrm{3}} \mathrm{x}\:\mathrm{csc}\:^{\mathrm{3}} \mathrm{x}\:\mathrm{dx}\: \\ $$$$ \\ $$
Commented by liberty last updated on 09/Nov/20
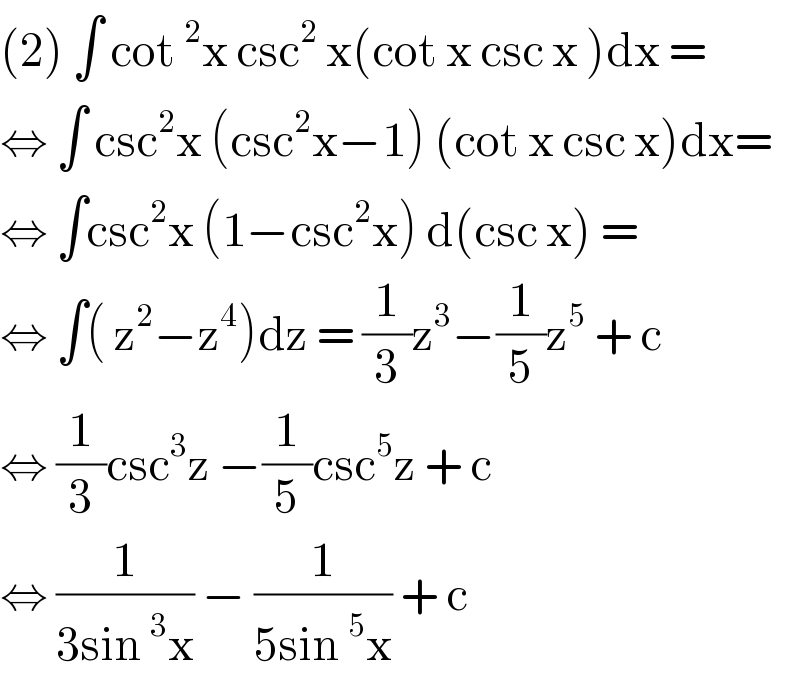
(2) ∫ cot^2 x csc^2 x(cot x csc x )dx = ⇔ ∫ csc^2 x (csc^2 x−1) (cot x csc x)dx= ⇔ ∫csc^2 x (1−csc^2 x) d(csc x) = ⇔ ∫( z^2 −z^4 )dz = (1/3)z^3 −(1/5)z^5 + c ⇔ (1/3)csc^3 z −(1/5)csc^5 z + c ⇔ (1/(3sin^3 x)) − (1/(5sin^5 x)) + c
$$\left(\mathrm{2}\right)\:\int\:\mathrm{cot}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{csc}^{\mathrm{2}} \:\mathrm{x}\left(\mathrm{cot}\:\mathrm{x}\:\mathrm{csc}\:\mathrm{x}\:\right)\mathrm{dx}\:= \\ $$$$\Leftrightarrow\:\int\:\mathrm{csc}^{\mathrm{2}} \mathrm{x}\:\left(\mathrm{csc}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\:\left(\mathrm{cot}\:\mathrm{x}\:\mathrm{csc}\:\mathrm{x}\right)\mathrm{dx}= \\ $$$$\Leftrightarrow\:\int\mathrm{csc}^{\mathrm{2}} \mathrm{x}\:\left(\mathrm{1}−\mathrm{csc}^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{d}\left(\mathrm{csc}\:\mathrm{x}\right)\:= \\ $$$$\Leftrightarrow\:\int\left(\:\mathrm{z}^{\mathrm{2}} −\mathrm{z}^{\mathrm{4}} \right)\mathrm{dz}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{z}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{5}}\mathrm{z}^{\mathrm{5}} \:+\:\mathrm{c}\: \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{csc}^{\mathrm{3}} \mathrm{z}\:−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{csc}^{\mathrm{5}} \mathrm{z}\:+\:\mathrm{c}\: \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{3sin}\:^{\mathrm{3}} \mathrm{x}}\:−\:\frac{\mathrm{1}}{\mathrm{5sin}\:^{\mathrm{5}} \mathrm{x}}\:+\:\mathrm{c}\: \\ $$
Commented by liberty last updated on 09/Nov/20
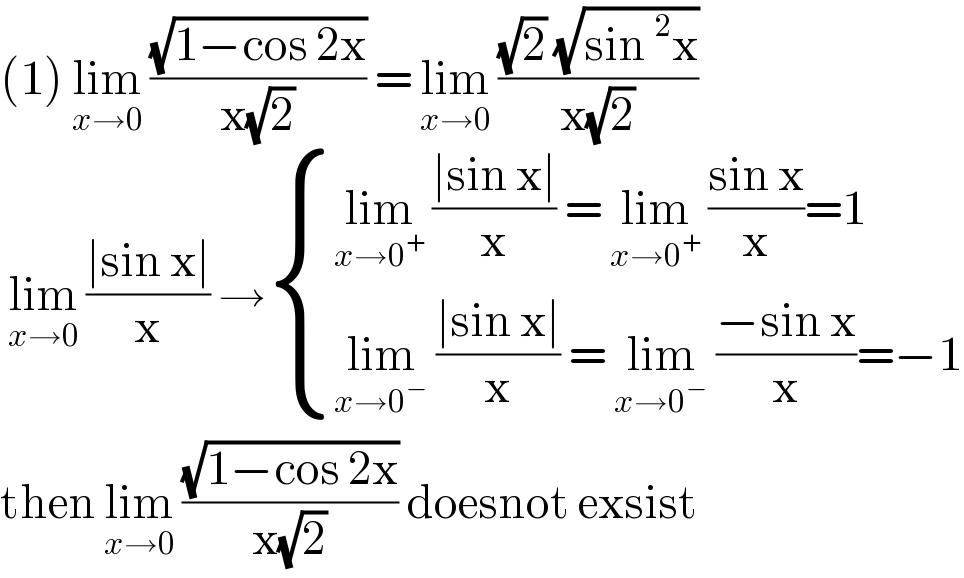
(1) lim_(x→0) ((√(1−cos 2x))/(x(√2))) = lim_(x→0) (((√2) (√(sin^2 x)))/(x(√2))) lim_(x→0) ((∣sin x∣)/x) → { ((lim_(x→0^+ ) ((∣sin x∣)/x) = lim_(x→0^+ ) ((sin x)/x)=1)),((lim_(x→0^− ) ((∣sin x∣)/x) = lim_(x→0^− ) ((−sin x)/x)=−1)) :} then lim_(x→0) ((√(1−cos 2x))/(x(√2))) doesnot exsist
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{2x}}}{\mathrm{x}\sqrt{\mathrm{2}}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}\:\sqrt{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}}{\mathrm{x}\sqrt{\mathrm{2}}} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mid\mathrm{sin}\:\mathrm{x}\mid}{\mathrm{x}}\:\rightarrow\begin{cases}{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mid\mathrm{sin}\:\mathrm{x}\mid}{\mathrm{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}=\mathrm{1}}\\{\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{\mid\mathrm{sin}\:\mathrm{x}\mid}{\mathrm{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}=−\mathrm{1}}\end{cases} \\ $$$$\mathrm{then}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{2x}}}{\mathrm{x}\sqrt{\mathrm{2}}}\:\mathrm{doesnot}\:\mathrm{exsist} \\ $$
Answered by Lordose last updated on 08/Nov/20
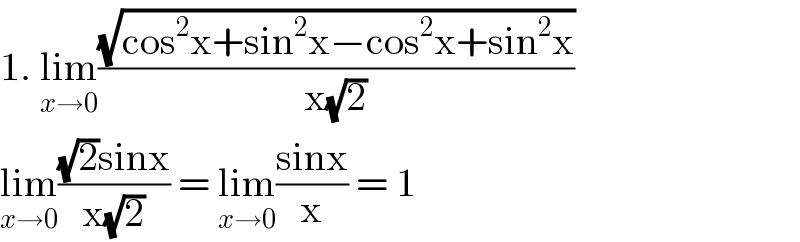
1. lim_(x→0) ((√(cos^2 x+sin^2 x−cos^2 x+sin^2 x))/(x(√2))) lim_(x→0) (((√2)sinx)/(x(√2))) = lim_(x→0) ((sinx)/x) = 1
$$\mathrm{1}.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}}{\mathrm{x}\sqrt{\mathrm{2}}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{2}}\mathrm{sinx}}{\mathrm{x}\sqrt{\mathrm{2}}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sinx}}{\mathrm{x}}\:=\:\mathrm{1} \\ $$
Commented by liberty last updated on 12/Nov/20
wrong
$$\mathrm{wrong} \\ $$
Answered by Lordose last updated on 08/Nov/20
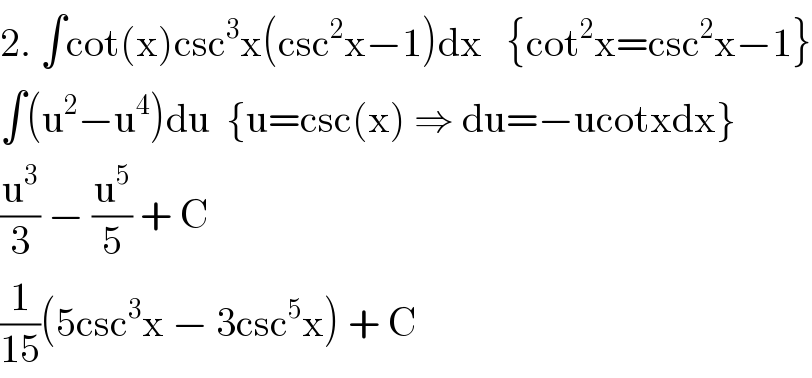
2. ∫cot(x)csc^3 x(csc^2 x−1)dx {cot^2 x=csc^2 x−1} ∫(u^2 −u^4 )du {u=csc(x) ⇒ du=−ucotxdx} (u^3 /3) − (u^5 /5) + C (1/(15))(5csc^3 x − 3csc^5 x) + C
$$\mathrm{2}.\:\int\mathrm{cot}\left(\mathrm{x}\right)\mathrm{csc}^{\mathrm{3}} \mathrm{x}\left(\mathrm{csc}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\mathrm{dx}\:\:\:\left\{\mathrm{cot}^{\mathrm{2}} \mathrm{x}=\mathrm{csc}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right\} \\ $$$$\int\left(\mathrm{u}^{\mathrm{2}} −\mathrm{u}^{\mathrm{4}} \right)\mathrm{du}\:\:\left\{\mathrm{u}=\mathrm{csc}\left(\mathrm{x}\right)\:\Rightarrow\:\mathrm{du}=−\mathrm{ucotxdx}\right\} \\ $$$$\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{3}}\:−\:\frac{\mathrm{u}^{\mathrm{5}} }{\mathrm{5}}\:+\:\mathrm{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{15}}\left(\mathrm{5csc}^{\mathrm{3}} \mathrm{x}\:−\:\mathrm{3csc}^{\mathrm{5}} \mathrm{x}\right)\:+\:\mathrm{C} \\ $$
Answered by Bird last updated on 09/Nov/20
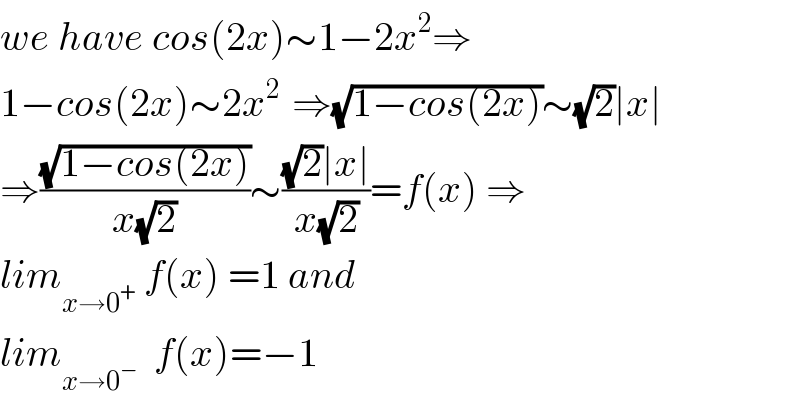
we have cos(2x)∼1−2x^2 ⇒ 1−cos(2x)∼2x^(2 ) ⇒(√(1−cos(2x)))∼(√2)∣x∣ ⇒((√(1−cos(2x)))/(x(√2)))∼(((√2)∣x∣)/(x(√2)))=f(x) ⇒ lim_(x→0^+ ) f(x) =1 and lim_(x→0^− ) f(x)=−1
$${we}\:{have}\:{cos}\left(\mathrm{2}{x}\right)\sim\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \Rightarrow \\ $$$$\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\sim\mathrm{2}{x}^{\mathrm{2}\:} \:\Rightarrow\sqrt{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}\sim\sqrt{\mathrm{2}}\mid{x}\mid \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}}{{x}\sqrt{\mathrm{2}}}\sim\frac{\sqrt{\mathrm{2}}\mid{x}\mid}{{x}\sqrt{\mathrm{2}}}={f}\left({x}\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{+} } \:{f}\left({x}\right)\:=\mathrm{1}\:{and}\:\:\:\: \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{−} } \:\:{f}\left({x}\right)=−\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *