Menu Close

1-lim-x-0-1-cos-6-2x-cos-3-3x-3x-2-2-lim-x-0-1-cos-4x-2sin-2-x-cos-4x-x-2-cos-3x-3-lim-x-pi-2-sin-x-2cos-2-x-1-sin-3-x-sin-x-

Tinku Tara 0 Comments
Pin




Question Number 115320 by john santu last updated on 25/Sep/20
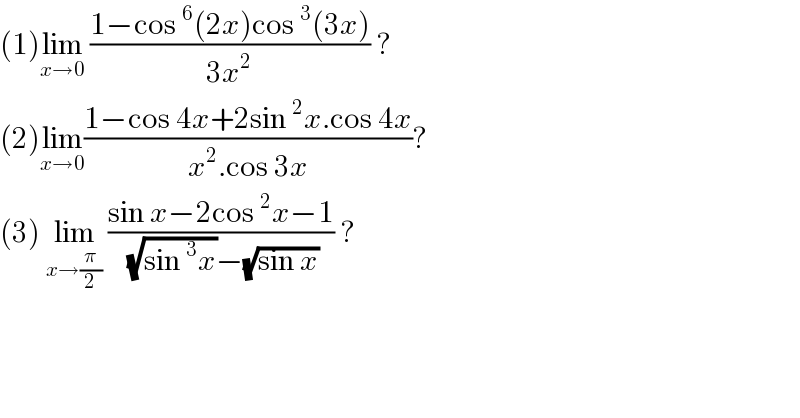
(1)lim_(x→0) ((1−cos^6 (2x)cos^3 (3x))/(3x^2 )) ? (2)lim_(x→0) ((1−cos 4x+2sin^2 x.cos 4x)/(x^2 .cos 3x))? (3) lim_(x→(π/2)) ((sin x−2cos^2 x−1)/( (√(sin^3 x))−(√(sin x)))) ?
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{6}} \left(\mathrm{2}{x}\right)\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{3}{x}\right)}{\mathrm{3}{x}^{\mathrm{2}} }\:? \\ $$$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{4}{x}+\mathrm{2sin}\:^{\mathrm{2}} {x}.\mathrm{cos}\:\mathrm{4}{x}}{{x}^{\mathrm{2}} .\mathrm{cos}\:\mathrm{3}{x}}? \\ $$$$\left(\mathrm{3}\right)\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}−\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}}{\:\sqrt{\mathrm{sin}\:^{\mathrm{3}} {x}}−\sqrt{\mathrm{sin}\:{x}}}\:?\: \\ $$
Answered by bobhans last updated on 29/Sep/20
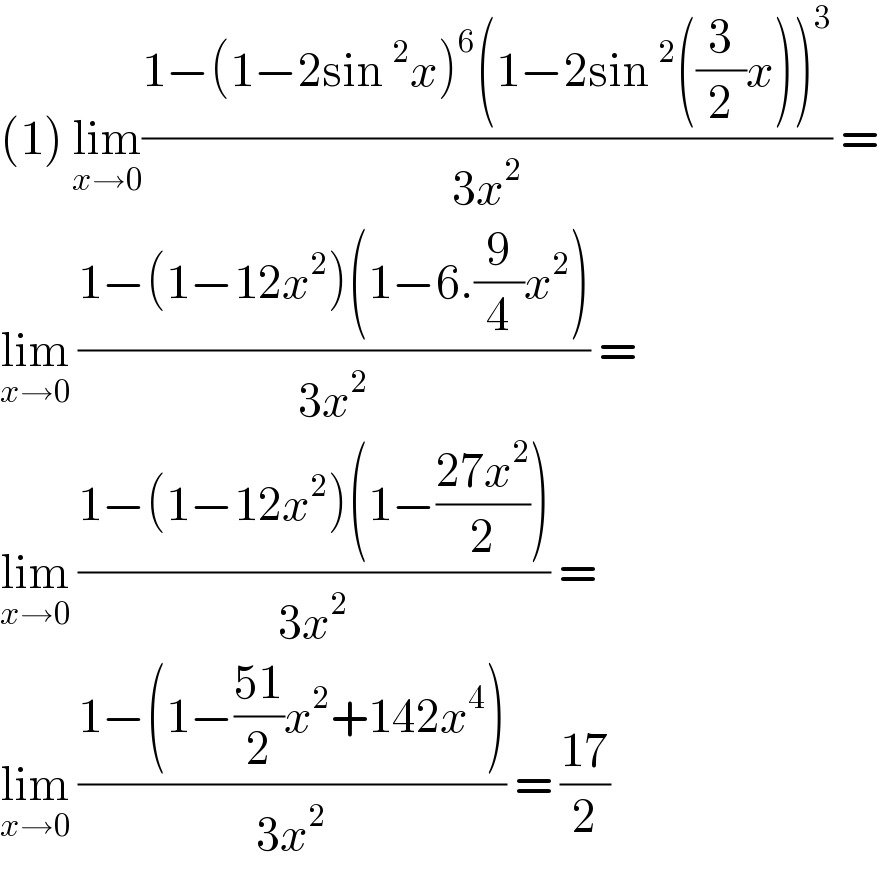
(1) lim_(x→0) ((1−(1−2sin^2 x)^6 (1−2sin^2 ((3/2)x))^3 )/(3x^2 )) = lim_(x→0) ((1−(1−12x^2 )(1−6.(9/4)x^2 ))/(3x^2 )) = lim_(x→0) ((1−(1−12x^2 )(1−((27x^2 )/2)))/(3x^2 )) = lim_(x→0) ((1−(1−((51)/2)x^2 +142x^4 ))/(3x^2 )) = ((17)/2)
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\right)^{\mathrm{6}} \left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}{x}\right)\right)^{\mathrm{3}} }{\mathrm{3}{x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{12}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{6}.\frac{\mathrm{9}}{\mathrm{4}}{x}^{\mathrm{2}} \right)}{\mathrm{3}{x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{12}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{27}{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{\mathrm{3}{x}^{\mathrm{2}} }\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{51}}{\mathrm{2}}{x}^{\mathrm{2}} +\mathrm{142}{x}^{\mathrm{4}} \right)}{\mathrm{3}{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{17}}{\mathrm{2}} \\ $$
Answered by bobhans last updated on 25/Sep/20
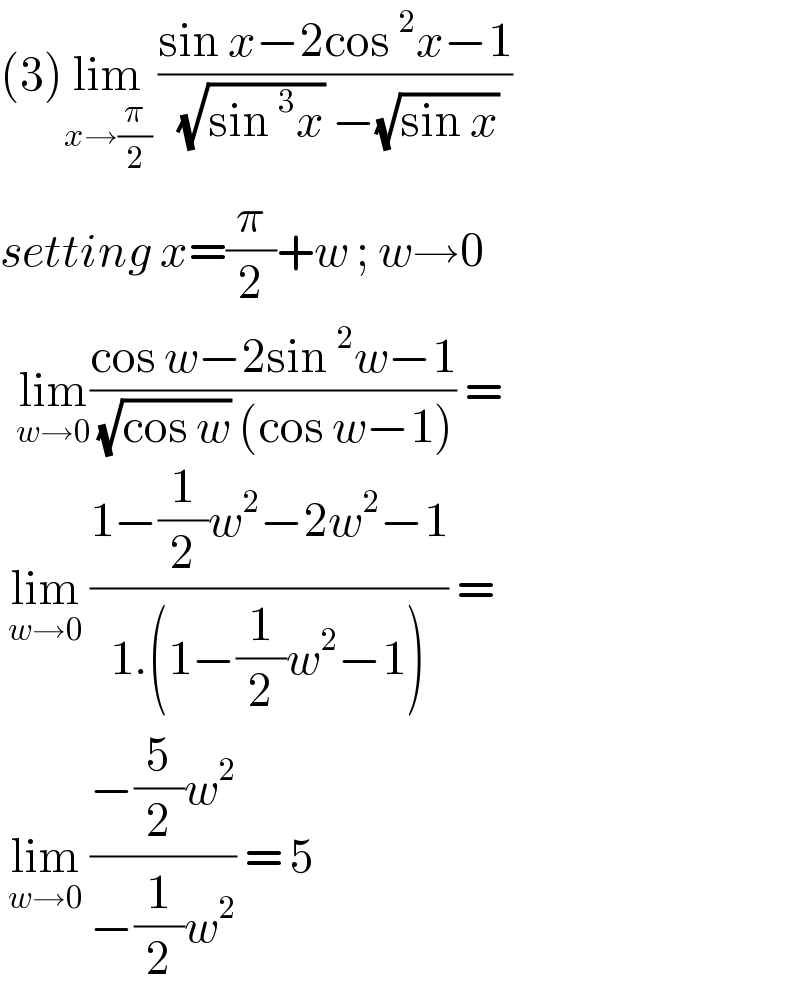
(3)lim_(x→(π/2)) ((sin x−2cos^2 x−1)/( (√(sin^3 x)) −(√(sin x)))) setting x=(π/2)+w ; w→0 lim_(w→0) ((cos w−2sin^2 w−1)/( (√(cos w)) (cos w−1))) = lim_(w→0) ((1−(1/2)w^2 −2w^2 −1)/(1.(1−(1/2)w^2 −1))) = lim_(w→0) ((−(5/2)w^2 )/(−(1/2)w^2 )) = 5
$$\left(\mathrm{3}\right)\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}−\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}}{\:\sqrt{\mathrm{sin}\:^{\mathrm{3}} {x}}\:−\sqrt{\mathrm{sin}\:{x}}}\: \\ $$$${setting}\:{x}=\frac{\pi}{\mathrm{2}}+{w}\:;\:{w}\rightarrow\mathrm{0} \\ $$$$\:\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{w}−\mathrm{2sin}\:^{\mathrm{2}} {w}−\mathrm{1}}{\:\sqrt{\mathrm{cos}\:{w}}\:\left(\mathrm{cos}\:{w}−\mathrm{1}\right)}\:=\: \\ $$$$\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{w}^{\mathrm{2}} −\mathrm{2}{w}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}.\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{w}^{\mathrm{2}} −\mathrm{1}\right)}\:=\: \\ $$$$\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{\mathrm{5}}{\mathrm{2}}{w}^{\mathrm{2}} }{−\frac{\mathrm{1}}{\mathrm{2}}{w}^{\mathrm{2}} }\:=\:\mathrm{5} \\ $$
Answered by bemath last updated on 25/Sep/20
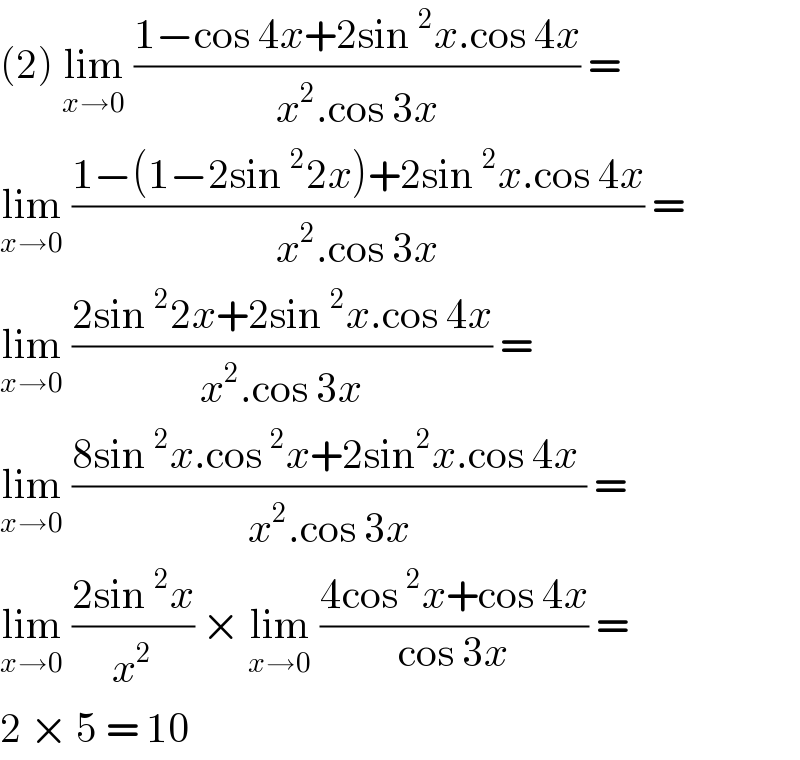
(2) lim_(x→0) ((1−cos 4x+2sin^2 x.cos 4x)/(x^2 .cos 3x)) = lim_(x→0) ((1−(1−2sin^2 2x)+2sin^2 x.cos 4x)/(x^2 .cos 3x)) = lim_(x→0) ((2sin^2 2x+2sin^2 x.cos 4x)/(x^2 .cos 3x)) = lim_(x→0) ((8sin^2 x.cos^2 x+2sin^2 x.cos 4x )/(x^2 .cos 3x)) = lim_(x→0) ((2sin^2 x)/x^2 ) × lim_(x→0) ((4cos^2 x+cos 4x)/(cos 3x)) = 2 × 5 = 10
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{4}{x}+\mathrm{2sin}\:^{\mathrm{2}} {x}.\mathrm{cos}\:\mathrm{4}{x}}{{x}^{\mathrm{2}} .\mathrm{cos}\:\mathrm{3}{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2}{x}\right)+\mathrm{2sin}\:^{\mathrm{2}} {x}.\mathrm{cos}\:\mathrm{4}{x}}{{x}^{\mathrm{2}} .\mathrm{cos}\:\mathrm{3}{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{2sin}\:^{\mathrm{2}} {x}.\mathrm{cos}\:\mathrm{4}{x}}{{x}^{\mathrm{2}} .\mathrm{cos}\:\mathrm{3}{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{8sin}\:^{\mathrm{2}} {x}.\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{2sin}^{\mathrm{2}} {x}.\mathrm{cos}\:\mathrm{4}{x}\:}{{x}^{\mathrm{2}} .\mathrm{cos}\:\mathrm{3}{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4cos}\:^{\mathrm{2}} {x}+\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{cos}\:\mathrm{3}{x}}\:= \\ $$$$\mathrm{2}\:×\:\mathrm{5}\:=\:\mathrm{10} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20
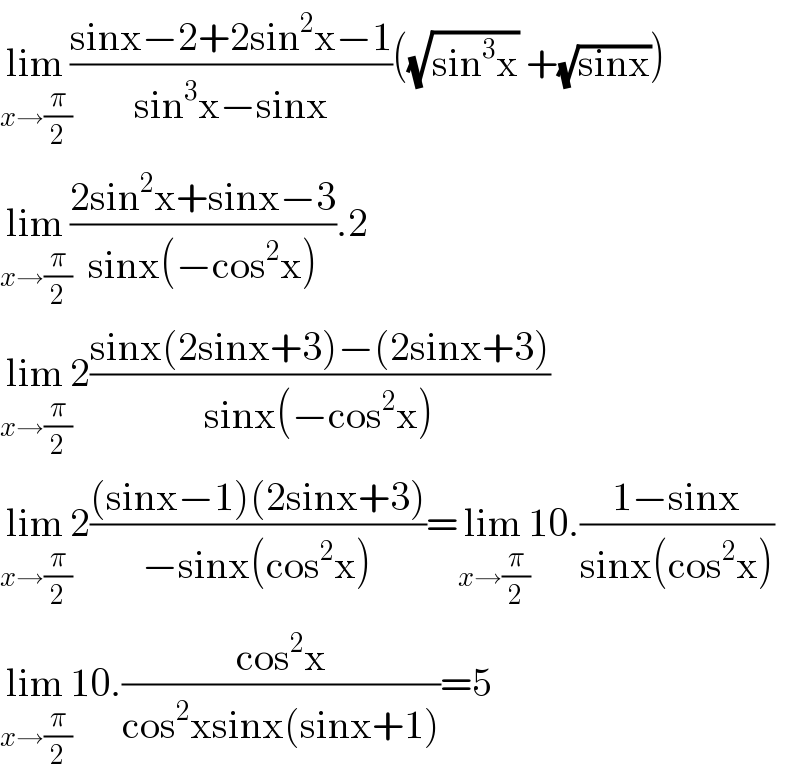
lim_(x→(π/2)) ((sinx−2+2sin^2 x−1)/(sin^3 x−sinx))((√(sin^3 x)) +(√(sinx))) lim_(x→(π/2)) ((2sin^2 x+sinx−3)/(sinx(−cos^2 x))).2 lim_(x→(π/2)) 2((sinx(2sinx+3)−(2sinx+3))/(sinx(−cos^2 x))) lim_(x→(π/2)) 2(((sinx−1)(2sinx+3))/(−sinx(cos^2 x)))=lim_(x→(π/2)) 10.((1−sinx)/(sinx(cos^2 x))) lim_(x→(π/2)) 10.((cos^2 x)/(cos^2 xsinx(sinx+1)))=5
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\frac{\mathrm{sinx}−\mathrm{2}+\mathrm{2sin}^{\mathrm{2}} \mathrm{x}−\mathrm{1}}{\mathrm{sin}^{\mathrm{3}} \mathrm{x}−\mathrm{sinx}}\left(\sqrt{\mathrm{sin}^{\mathrm{3}} \mathrm{x}}\:+\sqrt{\mathrm{sinx}}\right) \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\frac{\mathrm{2sin}^{\mathrm{2}} \mathrm{x}+\mathrm{sinx}−\mathrm{3}}{\mathrm{sinx}\left(−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)}.\mathrm{2} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}2}\frac{\mathrm{sinx}\left(\mathrm{2sinx}+\mathrm{3}\right)−\left(\mathrm{2sinx}+\mathrm{3}\right)}{\mathrm{sinx}\left(−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}2}\frac{\left(\mathrm{sinx}−\mathrm{1}\right)\left(\mathrm{2sinx}+\mathrm{3}\right)}{−\mathrm{sinx}\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)}=\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}10}.\frac{\mathrm{1}−\mathrm{sinx}}{\mathrm{sinx}\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}10}.\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}^{\mathrm{2}} \mathrm{xsinx}\left(\mathrm{sinx}+\mathrm{1}\right)}=\mathrm{5} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *