Question Number 161337 by bobhans last updated on 16/Dec/21
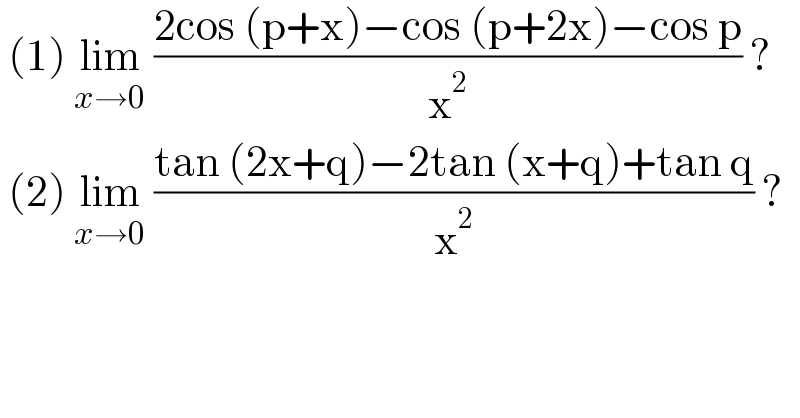
$$\:\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\left(\mathrm{p}+\mathrm{x}\right)−\mathrm{cos}\:\left(\mathrm{p}+\mathrm{2x}\right)−\mathrm{cos}\:\mathrm{p}}{\mathrm{x}^{\mathrm{2}} }\:? \\ $$$$\:\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\mathrm{2x}+\mathrm{q}\right)−\mathrm{2tan}\:\left(\mathrm{x}+\mathrm{q}\right)+\mathrm{tan}\:\mathrm{q}}{\mathrm{x}^{\mathrm{2}} }\:? \\ $$
Commented by cortano last updated on 16/Dec/21
![(1) lim_(x→0) ((2cos (p+x)−cos (p+2x)−cos p)/x^2 ) = lim_(x→0) ((2cos (p+x)−[ cos (p+2x)+cos p ])/x^2 ) = lim_(x→0) ((2cos (p+x)−2cos (p+x)cos x)/x^2 ) = lim_(x→0) ((2cos (p+x)[ 1−cos x ])/x^2 ) = 2cos p ×lim_(x→0) ((2sin^2 ((x/2)))/x^2 ) = 2cos p×(1/2)= cos p](https://www.tinkutara.com/question/Q161344.png)
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\left({p}+{x}\right)−\mathrm{cos}\:\left({p}+\mathrm{2}{x}\right)−\mathrm{cos}\:{p}}{{x}^{\mathrm{2}} }\: \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\left({p}+{x}\right)−\left[\:\mathrm{cos}\:\left({p}+\mathrm{2}{x}\right)+\mathrm{cos}\:{p}\:\right]}{{x}^{\mathrm{2}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\left({p}+{x}\right)−\mathrm{2cos}\:\left({p}+{x}\right)\mathrm{cos}\:{x}}{{x}^{\mathrm{2}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\left({p}+{x}\right)\left[\:\mathrm{1}−\mathrm{cos}\:{x}\:\right]}{{x}^{\mathrm{2}} } \\ $$$$\:=\:\mathrm{2cos}\:{p}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{{x}^{\mathrm{2}} } \\ $$$$\:=\:\mathrm{2cos}\:{p}×\frac{\mathrm{1}}{\mathrm{2}}=\:\mathrm{cos}\:{p} \\ $$
