Menu Close

1-lim-x-0-sin-x-ln-e-x-cos-x-x-sin-x-2-lim-x-1-1-x-ln-x-1-2x-x-2-

Tinku Tara 0 Comments
Pin




Question Number 111414 by bobhans last updated on 03/Sep/20
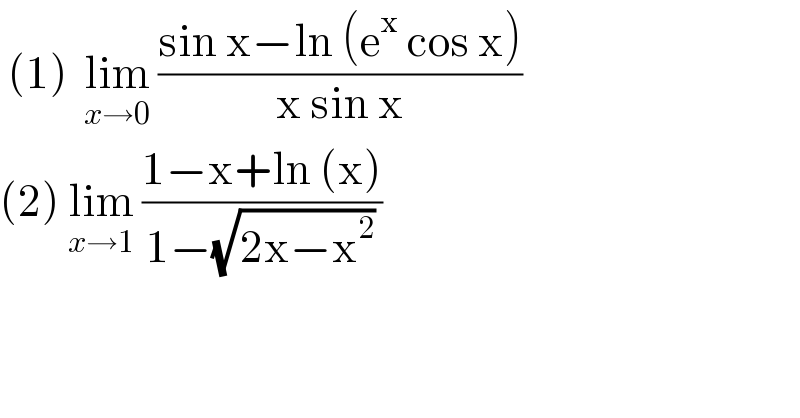
(1) lim_(x→0) ((sin x−ln (e^x cos x))/(x sin x)) (2) lim_(x→1) ((1−x+ln (x))/(1−(√(2x−x^2 ))))
$$\:\left(\mathrm{1}\right)\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{x}} \:\mathrm{cos}\:\mathrm{x}\right)}{\mathrm{x}\:\mathrm{sin}\:\mathrm{x}} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{x}+\mathrm{ln}\:\left(\mathrm{x}\right)}{\mathrm{1}−\sqrt{\mathrm{2x}−\mathrm{x}^{\mathrm{2}} }} \\ $$
Answered by john santu last updated on 03/Sep/20
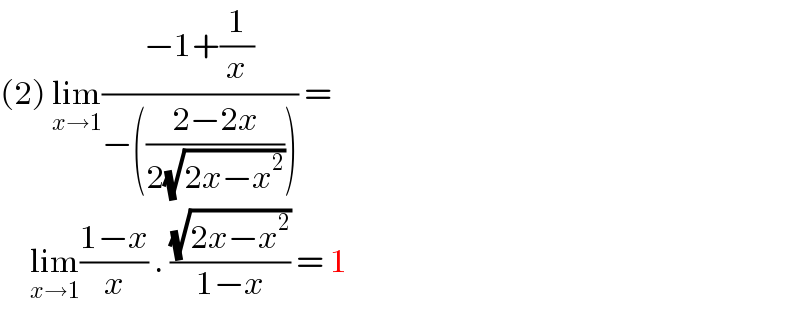
(2) lim_(x→1) ((−1+(1/x))/(−(((2−2x)/(2(√(2x−x^2 ))))))) = lim_(x→1) ((1−x)/x) . ((√(2x−x^2 ))/(1−x)) = 1
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{−\mathrm{1}+\frac{\mathrm{1}}{{x}}}{−\left(\frac{\mathrm{2}−\mathrm{2}{x}}{\mathrm{2}\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}\right)}\:= \\ $$$$\:\:\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}−{x}}{{x}}\:.\:\frac{\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}{\mathrm{1}−{x}}\:=\:\mathrm{1} \\ $$
Answered by john santu last updated on 03/Sep/20
(1) lim_(x→0) ((cos x−(((e^x cos x−e^x sin x)/(e^x cos x))))/(sin x+xcos x))= lim_(x→0) ((e^x cos^2 x−e^x cos x+e^x sin x)/(e^x cos x(sin x+xcos x)))= 1×lim_(x→0) ((cos^2 x−cos x+sin x)/(sin x+xcos x))= lim_(x→0) (((1−(x^2 /2))^2 −(1−(1/2)x^2 )+x−(x^3 /6))/(x−(x^3 /6)+x(1−(1/2)x^2 )))= lim_(x→0) ((x−(1/2)x^2 −(x^3 /6))/(2x−(1/3)x^3 )) = lim_(x→0) ((1−(1/2)x−(x^2 /6))/(2−(1/3)x^2 )) = (1/2).
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{x}−\left(\frac{{e}^{{x}} \mathrm{cos}\:{x}−{e}^{{x}} \mathrm{sin}\:{x}}{{e}^{{x}} \mathrm{cos}\:{x}}\right)}{\mathrm{sin}\:{x}+{x}\mathrm{cos}\:{x}}= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} \mathrm{cos}\:^{\mathrm{2}} {x}−{e}^{{x}} \mathrm{cos}\:{x}+{e}^{{x}} \mathrm{sin}\:{x}}{{e}^{{x}} \mathrm{cos}\:{x}\left(\mathrm{sin}\:{x}+{x}\mathrm{cos}\:{x}\right)}= \\ $$$$\:\mathrm{1}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}+{x}\mathrm{cos}\:{x}}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} −\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)+{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{x}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)}= \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}}{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *