Menu Close

1-lim-x-0-sinh-x-x-1-x-2-2-lim-x-0-x-ln-tan-x-

Tinku Tara 0 Comments
Pin




Question Number 112637 by bemath last updated on 09/Sep/20
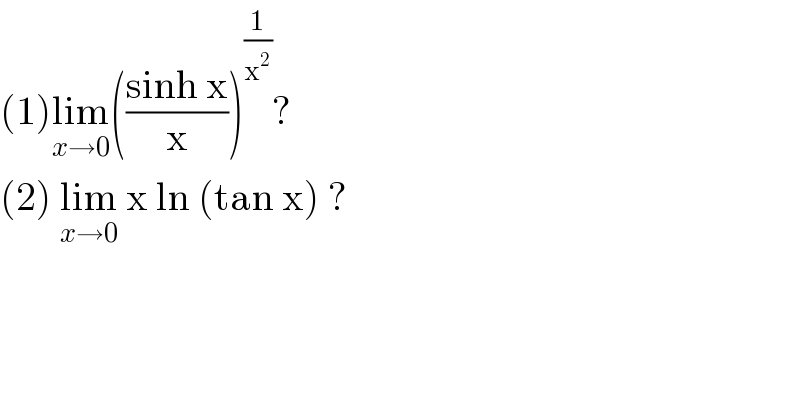
(1)lim_(x→0) (((sinh x)/x))^(1/x^2 ) ? (2) lim_(x→0) x ln (tan x) ?
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sinh}\:\mathrm{x}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} ? \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{x}\:\mathrm{ln}\:\left(\mathrm{tan}\:\mathrm{x}\right)\:? \\ $$
Answered by john santu last updated on 09/Sep/20
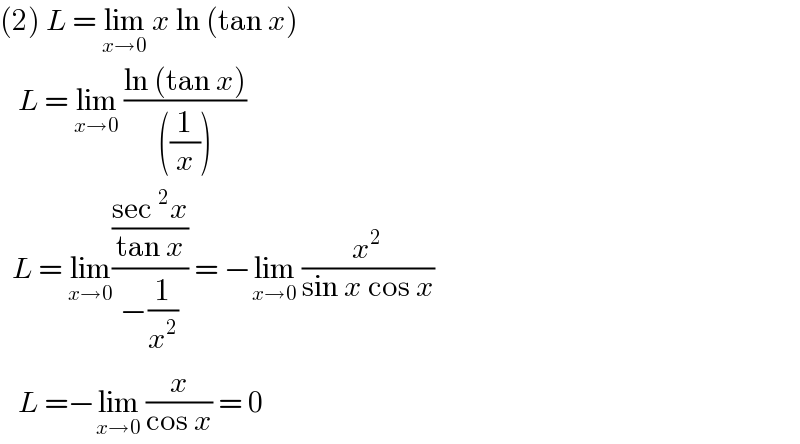
(2) L = lim_(x→0) x ln (tan x) L = lim_(x→0) ((ln (tan x))/(((1/x)))) L = lim_(x→0) (((sec^2 x)/(tan x))/(−(1/x^2 ))) = −lim_(x→0) (x^2 /(sin x cos x)) L =−lim_(x→0) (x/(cos x)) = 0
$$\left(\mathrm{2}\right)\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}\:\mathrm{ln}\:\left(\mathrm{tan}\:{x}\right)\: \\ $$$$\:\:\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{tan}\:{x}\right)}{\left(\frac{\mathrm{1}}{{x}}\right)} \\ $$$$\:\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{sec}\:^{\mathrm{2}} {x}}{\mathrm{tan}\:{x}}}{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:=\:−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} }{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}} \\ $$$$\:\:\:{L}\:=−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{\mathrm{cos}\:{x}}\:=\:\mathrm{0} \\ $$
Answered by john santu last updated on 09/Sep/20
(1) L=lim_(x→0) (((sinh x)/x))^(1/x^2 ) ln L = lim_(x→0) (1/x^2 )ln (((sinh x)/x)) ln L =lim_(x→0) ((ln (1+(x^2 /6)+(x^4 /(120))+...))/x^2 ) ln L = lim_(x→0) ((((d/dx)ln (1+(x^2 /6)+(x^4 /(120))+...))/(2x))) ln L =lim_(x→0) (1/(2x)). ((((2x)/6)+((4x^3 )/(120))+...)/(1+(x^2 /6)+(x^4 /(120))+...)) ln L = lim_(x→0) (((1/6)+((2x^3 )/(120))+...)/(1+(x^2 /6)+(x^4 /(120))+...)) ln L = (1/6) ⇒ L = (e)^(1/(6 )) .
$$\left(\mathrm{1}\right)\:{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sinh}\:{x}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$\:\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\mathrm{ln}\:\left(\frac{\mathrm{sinh}\:{x}}{{x}}\right) \\ $$$$\:\mathrm{ln}\:{L}\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+\frac{{x}^{\mathrm{4}} }{\mathrm{120}}+…\right)}{{x}^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\frac{{d}}{{dx}}\mathrm{ln}\:\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+\frac{{x}^{\mathrm{4}} }{\mathrm{120}}+…\right)}{\mathrm{2}{x}}\right) \\ $$$$\mathrm{ln}\:{L}\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}{x}}.\:\frac{\frac{\mathrm{2}{x}}{\mathrm{6}}+\frac{\mathrm{4}{x}^{\mathrm{3}} }{\mathrm{120}}+…}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+\frac{{x}^{\mathrm{4}} }{\mathrm{120}}+…} \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{2}{x}^{\mathrm{3}} }{\mathrm{120}}+…}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+\frac{{x}^{\mathrm{4}} }{\mathrm{120}}+…} \\ $$$$\mathrm{ln}\:{L}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow\:{L}\:=\:\sqrt[{\mathrm{6}\:}]{{e}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *