Question Number 167617 by mathlove last updated on 21/Mar/22
![(1)lim_(x→0) [tan((π/4)−x)]^(cotx) =? (2)lim_(x→0) [(1/(sin x))−(1/x)]=?](https://www.tinkutara.com/question/Q167617.png)
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[{tan}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right]^{{cotx}} =? \\ $$$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\mathrm{1}}{\mathrm{sin}\:{x}}−\frac{\mathrm{1}}{{x}}\right]=? \\ $$
Answered by cortano1 last updated on 21/Mar/22
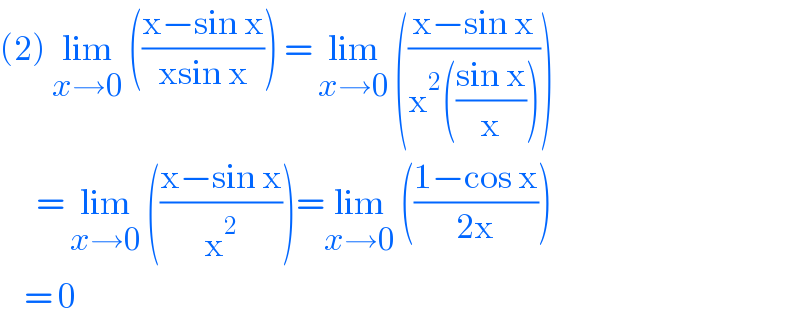
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{xsin}\:\mathrm{x}}\right)\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)}\right) \\ $$$$\:\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}{\mathrm{2x}}\right) \\ $$$$\:\:\:\:=\:\mathrm{0}\: \\ $$
Answered by LEKOUMA last updated on 21/Mar/22
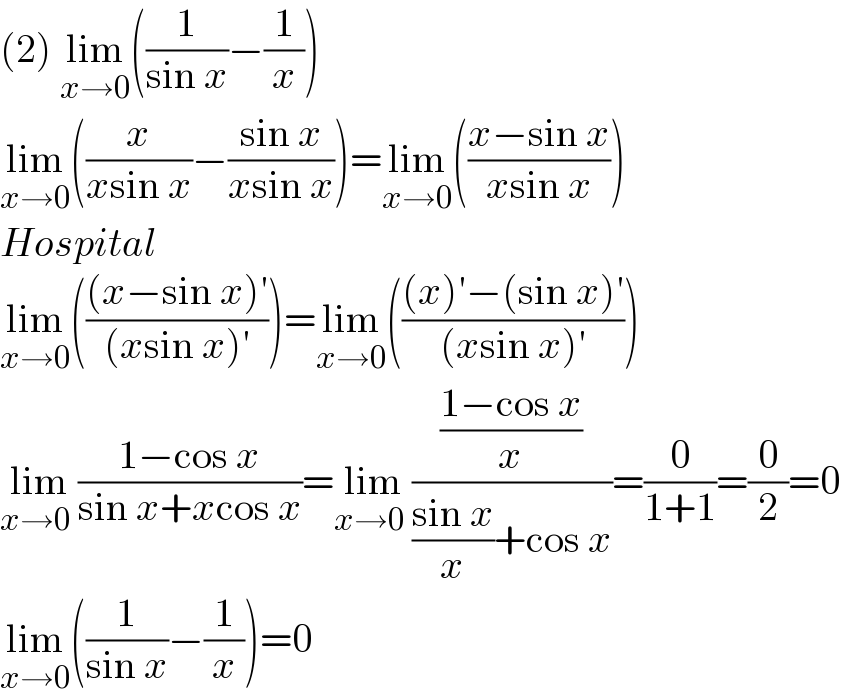
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{sin}\:{x}}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}}{{x}\mathrm{sin}\:{x}}−\frac{\mathrm{sin}\:{x}}{{x}\mathrm{sin}\:{x}}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}−\mathrm{sin}\:{x}}{{x}\mathrm{sin}\:{x}}\right) \\ $$$${Hospital} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left({x}−\mathrm{sin}\:{x}\right)'}{\left({x}\mathrm{sin}\:{x}\right)'}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left({x}\right)'−\left(\mathrm{sin}\:{x}\right)'}{\left({x}\mathrm{sin}\:{x}\right)'}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}\:\:} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+{x}\mathrm{cos}\:{x}}=\underset{{x}\rightarrow\mathrm{0}\:\:} {\mathrm{lim}}\frac{\frac{\mathrm{1}−\mathrm{cos}\:{x}}{{x}}}{\frac{\mathrm{sin}\:{x}}{{x}}+\mathrm{cos}\:{x}}=\frac{\mathrm{0}}{\mathrm{1}+\mathrm{1}}=\frac{\mathrm{0}}{\mathrm{2}}=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{sin}\:{x}}−\frac{\mathrm{1}}{{x}}\right)=\mathrm{0} \\ $$
Answered by qaz last updated on 21/Mar/22
![lim_(x→0) [tan ((π/4)−x)]^(cot x) =lim_(x→0) (((cot x−1)/(cot x+1)))^(cot x) =lim_(x→0) [(1−(2/(cot x+1)))^((cot x+1)/2) ]^2 (1−(2/(cot x+1)))^(−1) =e^(−2)](https://www.tinkutara.com/question/Q167642.png)
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\right]^{\mathrm{cot}\:\mathrm{x}} =\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{cot}\:\mathrm{x}−\mathrm{1}}{\mathrm{cot}\:\mathrm{x}+\mathrm{1}}\right)^{\mathrm{cot}\:\mathrm{x}} =\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{cot}\:\mathrm{x}+\mathrm{1}}\right)^{\frac{\mathrm{cot}\:\mathrm{x}+\mathrm{1}}{\mathrm{2}}} \right]^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{cot}\:\mathrm{x}+\mathrm{1}}\right)^{−\mathrm{1}} =\mathrm{e}^{−\mathrm{2}} \\ $$
