Question Number 128187 by john_santu last updated on 05/Jan/21
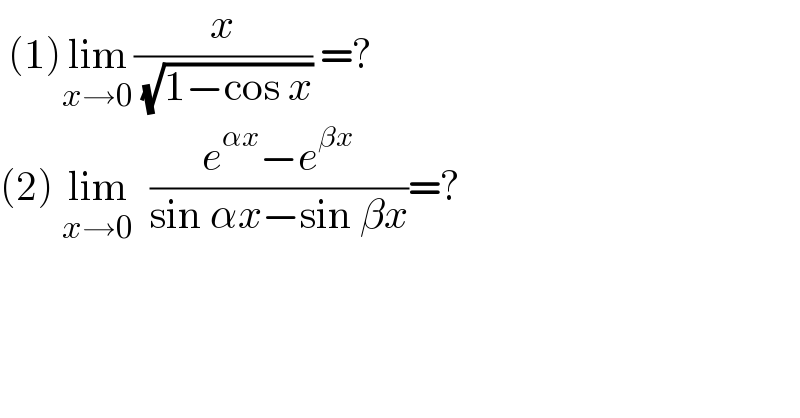
$$\:\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}}{\:\sqrt{\mathrm{1}−\mathrm{cos}\:{x}}}\:=?\: \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{{e}^{\alpha{x}} −{e}^{\beta{x}} }{\mathrm{sin}\:\alpha{x}−\mathrm{sin}\:\beta{x}}=? \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jan/21
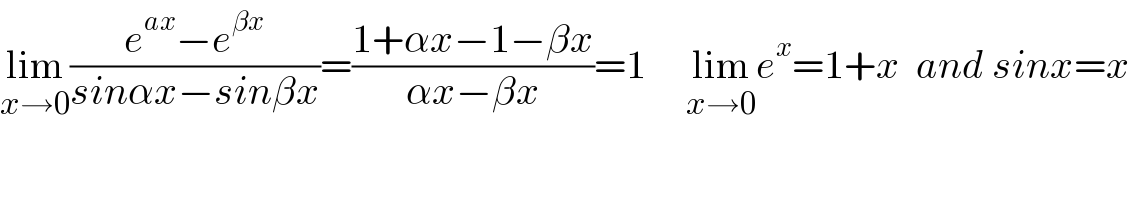
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{ax}} −{e}^{\beta{x}} }{{sin}\alpha{x}−{sin}\beta{x}}=\frac{\mathrm{1}+\alpha{x}−\mathrm{1}−\beta{x}}{\alpha{x}−\beta{x}}=\mathrm{1}\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{e}^{{x}} =\mathrm{1}+{x}\:\:{and}\:{sinx}={x} \\ $$
Answered by liberty last updated on 05/Jan/21
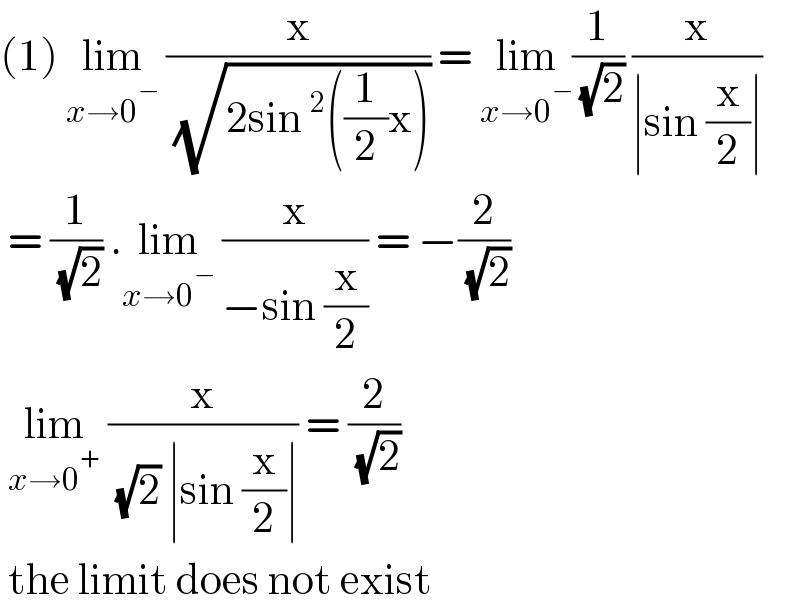
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}}\:=\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\frac{\mathrm{x}}{\mid\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mid} \\ $$$$\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:.\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{\mathrm{x}}{−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}}\:=\:−\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}\:\mid\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mid}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}} \\ $$$$\:\mathrm{the}\:\mathrm{limit}\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist}\: \\ $$
