Question Number 57442 by rahul 19 last updated on 04/Apr/19
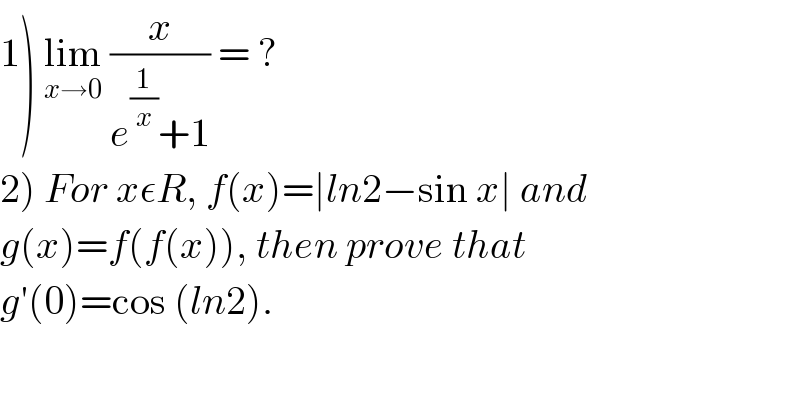
$$\left.\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}\:=\:? \\ $$$$\left.\mathrm{2}\right)\:{For}\:{x}\epsilon{R},\:{f}\left({x}\right)=\mid{ln}\mathrm{2}−\mathrm{sin}\:{x}\mid\:{and}\: \\ $$$${g}\left({x}\right)={f}\left({f}\left({x}\right)\right),\:{then}\:{prove}\:{that}\: \\ $$$${g}'\left(\mathrm{0}\right)=\mathrm{cos}\:\left({ln}\mathrm{2}\right). \\ $$
Commented by rahul 19 last updated on 04/Apr/19

$${in}\:{the}\:{neighbourhood}\:{of}\:\mathrm{0}, \\ $$$${which}\:{is}\:{greater}\:: \\ $$$${ln}\mathrm{2}\:{or}\:\mathrm{sin}\left({ln}\mathrm{2}−\mathrm{sin}\:{x}\right)\:? \\ $$$$\left({calulator}\:{not}\:{allowed}\right). \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Apr/19

$${whiout}\:{using}\:{graph}\:{app}\:{very}\:{difficult}\:{to}\:{reach} \\ $$$${the}\:{goal}… \\ $$
Commented by rahul 19 last updated on 04/Apr/19

$${ok}\:{sir}. \\ $$
Commented by kaivan.ahmadi last updated on 04/Apr/19
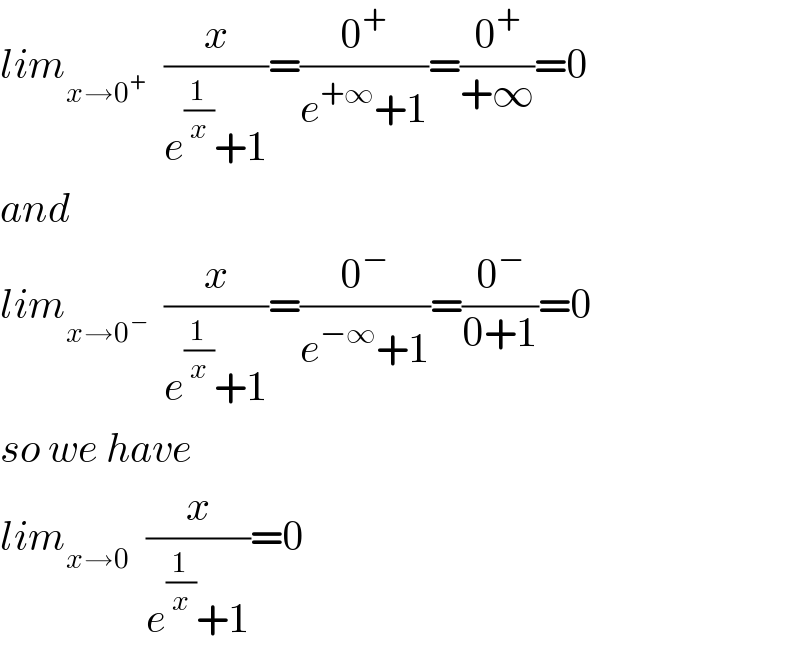
$${lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\frac{{x}}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}=\frac{\mathrm{0}^{+} }{{e}^{+\infty} +\mathrm{1}}=\frac{\mathrm{0}^{+} }{+\infty}=\mathrm{0} \\ $$$${and} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{−} } \:\:\frac{{x}}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}=\frac{\mathrm{0}^{−} }{{e}^{−\infty} +\mathrm{1}}=\frac{\mathrm{0}^{−} }{\mathrm{0}+\mathrm{1}}=\mathrm{0} \\ $$$${so}\:{we}\:{have} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{x}}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Apr/19
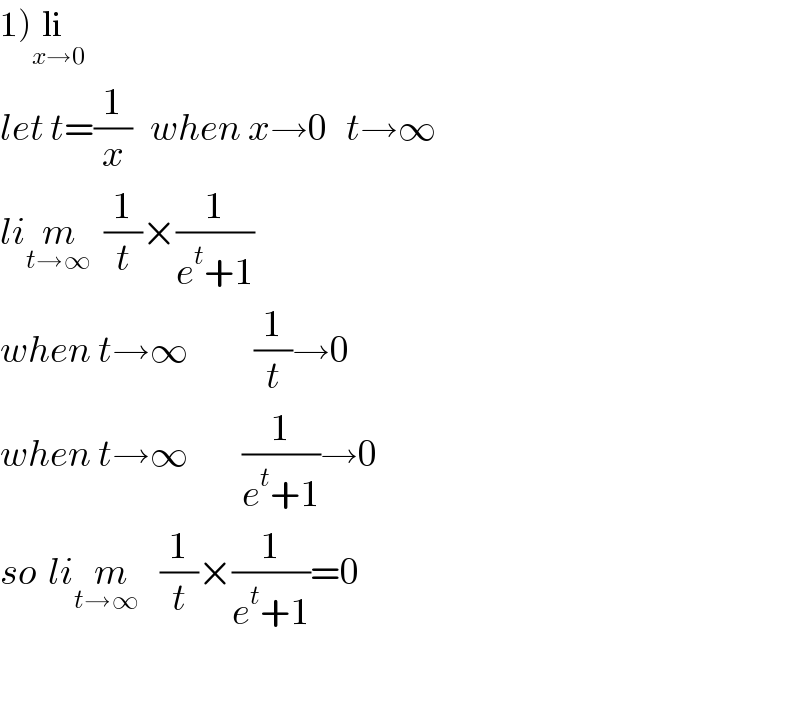
$$\left.\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$$${let}\:{t}=\frac{\mathrm{1}}{{x}}\:\:\:{when}\:{x}\rightarrow\mathrm{0}\:\:\:{t}\rightarrow\infty \\ $$$${li}\underset{{t}\rightarrow\infty} {{m}}\:\:\frac{\mathrm{1}}{{t}}×\frac{\mathrm{1}}{{e}^{{t}} +\mathrm{1}} \\ $$$${when}\:{t}\rightarrow\infty\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{t}}\rightarrow\mathrm{0} \\ $$$${when}\:{t}\rightarrow\infty\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{e}^{{t}} +\mathrm{1}}\rightarrow\mathrm{0} \\ $$$${so}\:\:{li}\underset{{t}\rightarrow\infty\:\:} {{m}}\:\:\frac{\mathrm{1}}{{t}}×\frac{\mathrm{1}}{{e}^{{t}} +\mathrm{1}}=\mathrm{0} \\ $$$$ \\ $$
Commented by rahul 19 last updated on 04/Apr/19

$${thanks}\:{sir}! \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Apr/19
![sinx value lies between ±1 we know ln2=0.6931 f(x)=ln2−sinx when ln2>sinx>0 =0 when sinx=ln2 =−(ln2−sinx) when 1>sinx>ln2 now look when sinx<0 then f(x)=∣ln2−sinx∣=(ln2−sinx) here we restrict to consider +ve value of sinx A)value of (dg/dx) when sinx<ln2 g(x)=f[f(x)] g(x)=f(ln2−sinx) when [ln2>sinx>0] =ln2−sin(ln2−sinx) ((dg(x))/dx)=0−cos(ln2−sinx)×(0−cosx) ((dg/dx))_(x=0) =−cos(ln2−0)×−1=cosln2 B) value of (dg/dx) when sinx=ln2 =f[f(x)] when sinx=ln2 =f[0] =ln2−sin0 =ln2 so (dg/dx)=0 at sinx=ln2 C) value of (dg/dx) when sinx>ln2 g(x)=f(−ln2+sinx) =ln2−sin(−ln2+sinx) (dg/dx)=0−cos(−ln2+sinx)×(0+cosx) ((dg/dx))_(x=0) =−cos(−ln2)=−cosln2](https://www.tinkutara.com/question/Q57457.png)
$${sinx}\:{value}\:{lies}\:{between}\:\pm\mathrm{1} \\ $$$${we}\:{know}\:{ln}\mathrm{2}=\mathrm{0}.\mathrm{6931} \\ $$$${f}\left({x}\right)={ln}\mathrm{2}−{sinx}\:\:\:\:\:\:\:\:\:\:\:\:\:{when}\:{ln}\mathrm{2}>{sinx}>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{when}\:{sinx}={ln}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−\left({ln}\mathrm{2}−{sinx}\right)\:\:\:\:{when}\:\mathrm{1}>{sinx}>{ln}\mathrm{2}\: \\ $$$$\:\:\:\:\:\:\:\:{now}\:{look}\:{when}\:{sinx}<\mathrm{0} \\ $$$$\:\:{then}\:{f}\left({x}\right)=\mid{ln}\mathrm{2}−{sinx}\mid=\left({ln}\mathrm{2}−{sinx}\right) \\ $$$${here}\:{we}\:{restrict}\:\:{to}\:{consider}\:\:+{ve}\:{value}\:{of} \\ $$$${sinx} \\ $$$$\left.{A}\right){value}\:{of}\:\frac{{dg}}{{dx}}\:\:{when}\:{sinx}<{ln}\mathrm{2} \\ $$$${g}\left({x}\right)={f}\left[{f}\left({x}\right)\right] \\ $$$${g}\left({x}\right)={f}\left({ln}\mathrm{2}−{sinx}\right)\:{when}\:\left[{ln}\mathrm{2}>{sinx}>\mathrm{0}\right] \\ $$$$\:\:\:\:\:\:\:\:\:={ln}\mathrm{2}−{sin}\left({ln}\mathrm{2}−{sinx}\right) \\ $$$$\:\frac{{dg}\left({x}\right)}{{dx}}=\mathrm{0}−{cos}\left({ln}\mathrm{2}−{sinx}\right)×\left(\mathrm{0}−{cosx}\right) \\ $$$$\left(\frac{{dg}}{{dx}}\right)_{{x}=\mathrm{0}} \:=−{cos}\left({ln}\mathrm{2}−\mathrm{0}\right)×−\mathrm{1}={cosln}\mathrm{2} \\ $$$$\left.{B}\right)\:{value}\:{of}\:\frac{{dg}}{{dx}}\:{when}\:{sinx}={ln}\mathrm{2} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:={f}\left[{f}\left({x}\right)\right]\:\:\:\:\:\:\:\:\:\:{when}\:{sinx}={ln}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:={f}\left[\mathrm{0}\right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:={ln}\mathrm{2}−{sin}\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:={ln}\mathrm{2} \\ $$$$ \\ $$$${so}\:\frac{{dg}}{{dx}}=\mathrm{0}\:\:{at}\:{sinx}={ln}\mathrm{2} \\ $$$$ \\ $$$$\left.{C}\right)\:{value}\:{of}\:\frac{{dg}}{{dx}}\:{when}\:{sinx}>{ln}\mathrm{2} \\ $$$${g}\left({x}\right)={f}\left(−{ln}\mathrm{2}+{sinx}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:={ln}\mathrm{2}−{sin}\left(−{ln}\mathrm{2}+{sinx}\right) \\ $$$$\frac{{dg}}{{dx}}=\mathrm{0}−{cos}\left(−{ln}\mathrm{2}+{sinx}\right)×\left(\mathrm{0}+{cosx}\right) \\ $$$$\:\:\:\:\:\:\left(\frac{{dg}}{{dx}}\right)_{{x}=\mathrm{0}} =−{cos}\left(−{ln}\mathrm{2}\right)=−{cosln}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Apr/19

