Menu Close

1-lim-x-1-arc-sin-1-x-1-x-2-lim-x-e-x-3-cos-1-x-2-3-lim-x-0-csc-x-sin-sin-x-

Tinku Tara 0 Comments
Pin




Question Number 115162 by john santu last updated on 24/Sep/20
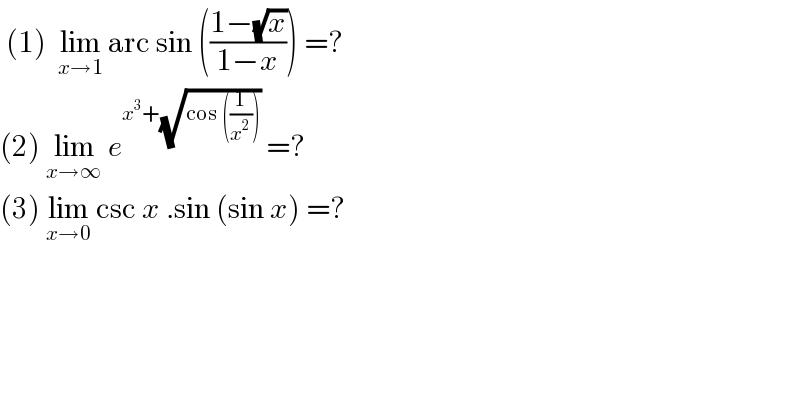
(1) lim_(x→1) arc sin (((1−(√x))/(1−x))) =? (2) lim_(x→∞) e^(x^3 +(√(cos ((1/x^2 ))))) =? (3) lim_(x→0) csc x .sin (sin x) =?
$$\:\left(\mathrm{1}\right)\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\mathrm{arc}\:\mathrm{sin}\:\left(\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}−{x}}\right)\:=? \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{e}^{{x}^{\mathrm{3}} +\sqrt{\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}} \:=? \\ $$$$\left(\mathrm{3}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{csc}\:{x}\:.\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)\:=? \\ $$
Answered by bobhans last updated on 24/Sep/20
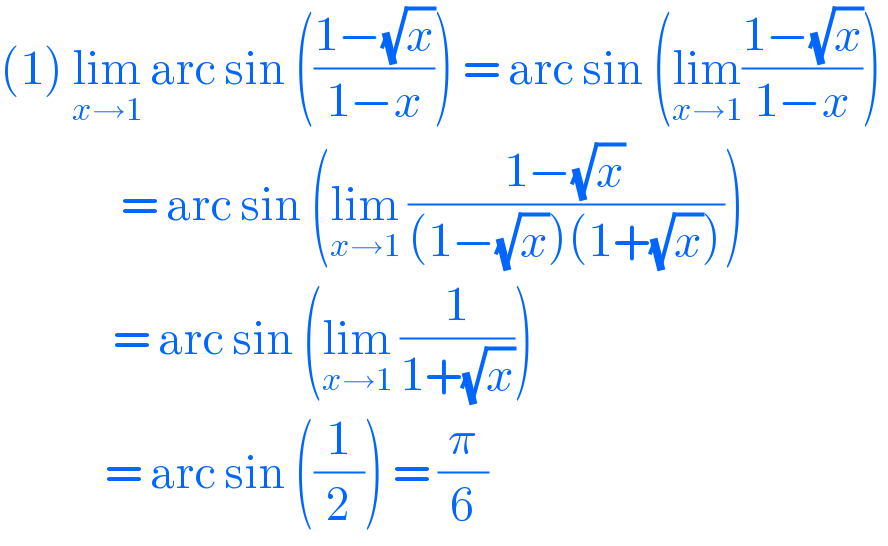
(1) lim_(x→1) arc sin (((1−(√x))/(1−x))) = arc sin (lim_(x→1) ((1−(√x))/(1−x))) = arc sin (lim_(x→1) ((1−(√x))/((1−(√x))(1+(√x))))) = arc sin (lim_(x→1) (1/(1+(√x)))) = arc sin ((1/2)) = (π/6)
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\mathrm{arc}\:\mathrm{sin}\:\left(\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}−{x}}\right)\:=\:\mathrm{arc}\:\mathrm{sin}\:\left(\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}−{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{arc}\:\mathrm{sin}\:\left(\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}−\sqrt{{x}}}{\left(\mathrm{1}−\sqrt{{x}}\right)\left(\mathrm{1}+\sqrt{{x}}\right)}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{arc}\:\mathrm{sin}\:\left(\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{1}+\sqrt{{x}}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{arc}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\pi}{\mathrm{6}} \\ $$
Answered by bobhans last updated on 24/Sep/20
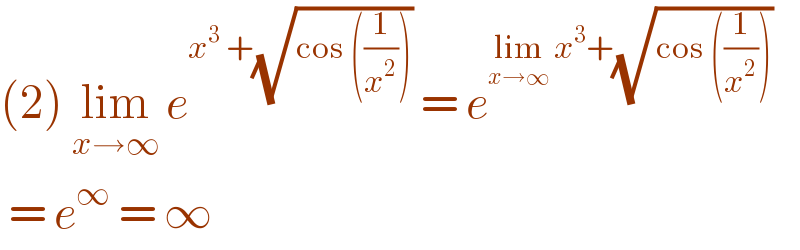
(2) lim_(x→∞) e^(x^3 +(√(cos ((1/x^2 ))))) = e^(lim_(x→∞) x^3 +(√(cos ((1/x^2 ))))) = e^∞ = ∞
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{e}^{{x}^{\mathrm{3}} \:+\sqrt{\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}} \:=\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{3}} +\sqrt{\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}} \\ $$$$\:=\:{e}^{\infty} \:=\:\infty\: \\ $$
Answered by bobhans last updated on 24/Sep/20
(3) lim_(x→0) csc x. sin (sin x) = lim_(x→0) ((sin (sin x))/(sin x)) [ let sin x = w ; w→0 ] lim_(x→0) ((sin (sin x))/(sin x)) = lim_(w→0) ((sin (w))/w) = 1
$$\left(\mathrm{3}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{csc}\:{x}.\:\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)}{\mathrm{sin}\:{x}} \\ $$$$\left[\:{let}\:\mathrm{sin}\:{x}\:=\:{w}\:;\:{w}\rightarrow\mathrm{0}\:\right] \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)}{\mathrm{sin}\:{x}}\:=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left({w}\right)}{{w}}\:=\:\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 24/Sep/20
lim_(x→1) sin^(−1) (((1−(√x))/(1+x)))=sin^(−1) ((1/(1+(√x))))=(π/6)
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\sqrt{\mathrm{x}}}{\mathrm{1}+\mathrm{x}}\right)=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{x}}}\right)=\frac{\pi}{\mathrm{6}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *