Menu Close

1-lim-x-i-2-z-i-2-2z-i-3-z-2-lim-x-e-pii-4-2z-2-z-3-z-1-3-lim-x-2i-2z-2-8-z-4-3-64-4-lim-x-0-cos-4z-1-z-sin-z-

Tinku Tara 0 Comments
Pin




Question Number 51214 by gunawan last updated on 25/Dec/18
1.lim_(x→−(i/2)) (((z−i)^2 )/((2z−i)(3−z))) 2.lim_(x→e^((πi)/4) ) ((2z^2 )/(z^3 −z−1)) 3.lim_(x→2i) ((2z^2 +8)/( (√z^4 )−^3 (√(64)))) 4.lim_(x→0) ((cos 4z−1)/(z sin z))
$$\mathrm{1}.\underset{{x}\rightarrow−\frac{\mathrm{i}}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\left({z}−{i}\right)^{\mathrm{2}} }{\left(\mathrm{2}{z}−{i}\right)\left(\mathrm{3}−{z}\right)} \\ $$$$\mathrm{2}.\underset{{x}\rightarrow{e}^{\frac{\pi{i}}{\mathrm{4}}} } {\mathrm{lim}}\:\frac{\mathrm{2}{z}^{\mathrm{2}} }{{z}^{\mathrm{3}} −{z}−\mathrm{1}} \\ $$$$\mathrm{3}.\underset{{x}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\frac{\mathrm{2}{z}^{\mathrm{2}} +\mathrm{8}}{\:\sqrt{{z}^{\mathrm{4}} }−^{\mathrm{3}} \sqrt{\mathrm{64}}} \\ $$$$\mathrm{4}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{4}{z}−\mathrm{1}}{{z}\:\mathrm{sin}\:{z}} \\ $$$$ \\ $$
Answered by afachri last updated on 25/Dec/18
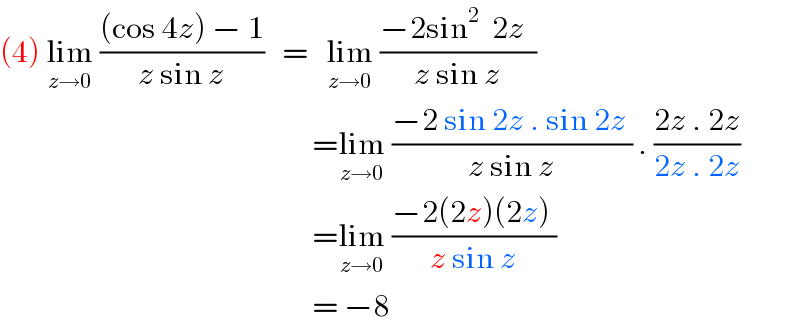
(4) lim_(z→0) (((cos 4z) − 1)/(z sin z)) = lim_(z→0) ((−2sin^2 2z )/(z sin z)) =lim_(z→0) ((−2 sin 2z . sin 2z )/(z sin z)) . ((2z . 2z)/(2z . 2z)) =lim_(z→0) ((−2(2z)(2z) )/(z sin z)) = −8
$$\left(\mathrm{4}\right)\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{cos}\:\mathrm{4}{z}\right)\:−\:\mathrm{1}}{{z}\:\mathrm{sin}\:{z}}\:\:\:=\:\:\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2sin}^{\mathrm{2}} \:\:\mathrm{2}{z}\:\:}{{z}\:\mathrm{sin}\:{z}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2}\:\mathrm{sin}\:\mathrm{2}{z}\:.\:\mathrm{sin}\:\mathrm{2}{z}\:}{{z}\:\mathrm{sin}\:{z}}\:.\:\frac{\mathrm{2}{z}\:.\:\mathrm{2}{z}}{\mathrm{2}{z}\:.\:\mathrm{2}{z}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2}\left(\mathrm{2}{z}\right)\left(\mathrm{2}{z}\right)\:}{{z}\:\mathrm{sin}\:{z}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{8} \\ $$
Answered by afachri last updated on 25/Dec/18
(3) know : i = (√(−1)) i^2 = −1 i^4 = 1 lim_(x→2i) ((2x^2 + 8 )/( (√(x^4 )) − ((64^ ))^(1/3) )) = lim_(x→2i) ((2(x^2 + 4) )/( (√x^4 ) − 4)) . (((√(x^4 ))+ 4 )/( (√(x^4 ))+ 4 )) = lim_(x→2i) ((2(x^2 + 4)((√(x^4 ))+ 4) )/(x^4 − 16)) = lim_(x→2i) ((2(x^2 + 4)((√x^4 ) + 4))/((x^2 + 4)(x^2 − 4))) = lim_(x→2i) ((2((√(x^4 ))+ 4))/(x^2 − 4)) = lim_(x→2i) ((2((√((2i)^4^ ))+ 4))/((2i)^2 − 4)) = lim_(x→2i) ((2((√(16i^( 4^ ) ))+ 4))/(4 i^2 − 4)) = ((2×8)/(−8)) = −2
$$\left(\mathrm{3}\right)\:\mathrm{know}\::\:\:{i}\:=\:\sqrt{−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{i}^{\mathrm{2}} =\:−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{i}^{\mathrm{4}} =\:\:\:\mathrm{1}\:\:\:\:\:\:\: \\ $$$$\underset{{x}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\:\:\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} +\:\mathrm{8}\:}{\:\sqrt{{x}^{\mathrm{4}} \:}\:−\:\sqrt[{\mathrm{3}}]{\mathrm{64}^{} }\:}\:\:\:\:\:\:\:=\:\:\:\:\underset{{x}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\:\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\:\mathrm{4}\right)\:}{\:\sqrt{{x}^{\mathrm{4}} }\:−\:\mathrm{4}}\:.\:\frac{\sqrt{{x}^{\mathrm{4}} \:}+\:\mathrm{4}\:\:}{\:\sqrt{{x}^{\mathrm{4}} \:}+\:\mathrm{4}\:} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\:\:\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\:\mathrm{4}\right)\left(\sqrt{{x}^{\mathrm{4}} \:}+\:\mathrm{4}\right)\:}{{x}^{\mathrm{4}} −\:\mathrm{16}}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\:\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\:\mathrm{4}\right)\left(\sqrt{{x}^{\mathrm{4}} }\:+\:\:\mathrm{4}\right)}{\left({x}^{\mathrm{2}} +\:\mathrm{4}\right)\left({x}^{\mathrm{2}} −\:\mathrm{4}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\underset{{x}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\:\:\frac{\mathrm{2}\left(\sqrt{{x}^{\mathrm{4}} \:}+\:\mathrm{4}\right)}{{x}^{\mathrm{2}} −\:\mathrm{4}}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\:\frac{\mathrm{2}\left(\sqrt{\left(\mathrm{2}{i}\right)^{\mathrm{4}^{} } }+\:\mathrm{4}\right)}{\left(\mathrm{2}{i}\right)^{\mathrm{2}} −\:\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\sqrt{\mathrm{16}{i}^{\:\mathrm{4}^{} } }+\:\mathrm{4}\right)}{\mathrm{4}\:{i}^{\mathrm{2}} −\:\mathrm{4}}\:=\:\frac{\mathrm{2}×\mathrm{8}}{−\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{2} \\ $$$$ \\ $$
Commented by gunawan last updated on 25/Dec/18
thank you Sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
Commented by afachri last updated on 25/Dec/18
ur welcome, Sir.
$$\mathrm{ur}\:\mathrm{welcome},\:\mathrm{Sir}.\:\: \\ $$
Answered by malwaan last updated on 25/Dec/18
(4)lim_(z→0) (((cos4z−1)(cos4z+1))/(z sinz(cos4z+1))) =lim_(z→0) ((cos^2 4z−1)/(z sinz(cos4z+1))) =lim_(z→0) ((−sin^2 4z)/(z sinz(cos4z+1))) =lim_(z→0) ((−2[2sinz cosz]cos2z×2[2sinz cosz]cos2z)/(z sinz(cos4z+1))) =((−2×2×2×2)/2) =−8
$$\left(\mathrm{4}\right)\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \frac{\left(\mathrm{cos4z}−\mathrm{1}\right)\left(\mathrm{cos4z}+\mathrm{1}\right)}{\mathrm{z}\:\mathrm{sinz}\left(\mathrm{cos4z}+\mathrm{1}\right)} \\ $$$$=\mathrm{li}\underset{\mathrm{z}\rightarrow\mathrm{0}} {\mathrm{m}}\:\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{4z}−\mathrm{1}}{\mathrm{z}\:\mathrm{sinz}\left(\mathrm{cos4z}+\mathrm{1}\right)} \\ $$$$=\mathrm{li}\underset{\mathrm{z}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{−\mathrm{sin}^{\mathrm{2}} \mathrm{4z}}{\mathrm{z}\:\mathrm{sinz}\left(\mathrm{cos4z}+\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \frac{−\mathrm{2}\left[\mathrm{2sinz}\:\mathrm{cosz}\right]\mathrm{cos2z}×\mathrm{2}\left[\mathrm{2sinz}\:\mathrm{cosz}\right]\mathrm{cos2z}}{\mathrm{z}\:\mathrm{sinz}\left(\mathrm{cos4z}+\mathrm{1}\right)} \\ $$$$=\frac{−\mathrm{2}×\mathrm{2}×\mathrm{2}×\mathrm{2}}{\mathrm{2}}\:=−\mathrm{8} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *