Menu Close

1-lim-x-p-p-x-x-p-x-x-p-p-2-There-are-4-identical-math-books-2-identical-physics-books-and-2-identical-chemistry-books-How-many-ways-to-compile-the-eight-books-on-the-condition-o

Tinku Tara 0 Comments
Pin




Question Number 112455 by john santu last updated on 08/Sep/20
(1)lim_(x→p) ((p^x −x^p )/(x^x −p^p )) ? (2) There are 4 identical math books, 2 identical physics books and 2 identical chemistry books. How many ways to compile the eight books on the condition of the same books are not mutually adjacent?
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{p}} {\mathrm{lim}}\:\frac{\mathrm{p}^{\mathrm{x}} −\mathrm{x}^{\mathrm{p}} }{\mathrm{x}^{\mathrm{x}} −\mathrm{p}^{\mathrm{p}} }\:?\: \\ $$$$\left(\mathrm{2}\right)\:{There}\:{are}\:\mathrm{4}\:{identical}\:{math}\:{books}, \\ $$$$\mathrm{2}\:{identical}\:{physics}\:{books}\:{and}\:\mathrm{2}\:{identical} \\ $$$${chemistry}\:{books}.\:{How}\:{many}\:{ways}\:{to} \\ $$$${compile}\:{the}\:{eight}\:{books}\:{on}\:{the}\: \\ $$$${condition}\:{of}\:{the}\:{same}\:{books}\:{are}\:{not} \\ $$$${mutually}\:{adjacent}? \\ $$
Answered by bobhans last updated on 08/Sep/20
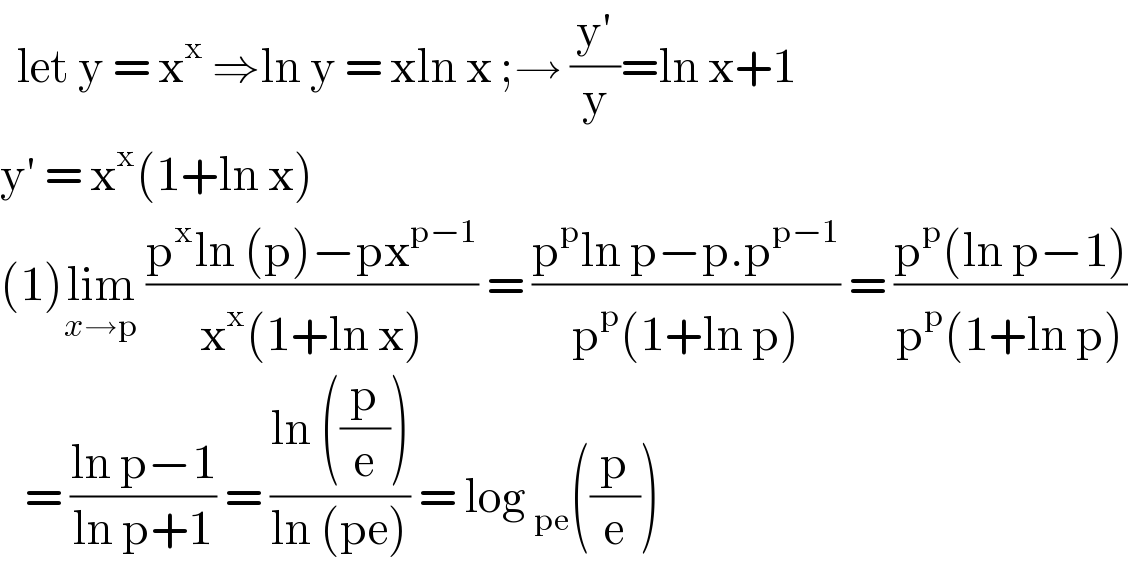
let y = x^x ⇒ln y = xln x ;→ ((y′)/y)=ln x+1 y′ = x^x (1+ln x) (1)lim_(x→p) ((p^x ln (p)−px^(p−1) )/(x^x (1+ln x))) = ((p^p ln p−p.p^(p−1) )/(p^p (1+ln p))) = ((p^p (ln p−1))/(p^p (1+ln p))) = ((ln p−1)/(ln p+1)) = ((ln ((p/e)))/(ln (pe))) = log _(pe) ((p/e))
$$\:\:\mathrm{let}\:\mathrm{y}\:=\:\mathrm{x}^{\mathrm{x}} \:\Rightarrow\mathrm{ln}\:\mathrm{y}\:=\:\mathrm{xln}\:\mathrm{x}\:;\rightarrow\:\frac{\mathrm{y}'}{\mathrm{y}}=\mathrm{ln}\:\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{y}'\:=\:\mathrm{x}^{\mathrm{x}} \left(\mathrm{1}+\mathrm{ln}\:\mathrm{x}\right) \\ $$$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{p}} {\mathrm{lim}}\:\frac{\mathrm{p}^{\mathrm{x}} \mathrm{ln}\:\left(\mathrm{p}\right)−\mathrm{px}^{\mathrm{p}−\mathrm{1}} }{\mathrm{x}^{\mathrm{x}} \left(\mathrm{1}+\mathrm{ln}\:\mathrm{x}\right)}\:=\:\frac{\mathrm{p}^{\mathrm{p}} \mathrm{ln}\:\mathrm{p}−\mathrm{p}.\mathrm{p}^{\mathrm{p}−\mathrm{1}} }{\mathrm{p}^{\mathrm{p}} \left(\mathrm{1}+\mathrm{ln}\:\mathrm{p}\right)}\:=\:\frac{\mathrm{p}^{\mathrm{p}} \left(\mathrm{ln}\:\mathrm{p}−\mathrm{1}\right)}{\mathrm{p}^{\mathrm{p}} \left(\mathrm{1}+\mathrm{ln}\:\mathrm{p}\right)} \\ $$$$\:\:\:=\:\frac{\mathrm{ln}\:\mathrm{p}−\mathrm{1}}{\mathrm{ln}\:\mathrm{p}+\mathrm{1}}\:=\:\frac{\mathrm{ln}\:\left(\frac{\mathrm{p}}{\mathrm{e}}\right)}{\mathrm{ln}\:\left(\mathrm{pe}\right)}\:=\:\mathrm{log}\:_{\mathrm{pe}} \left(\frac{\mathrm{p}}{\mathrm{e}}\right) \\ $$
Answered by mr W last updated on 08/Sep/20
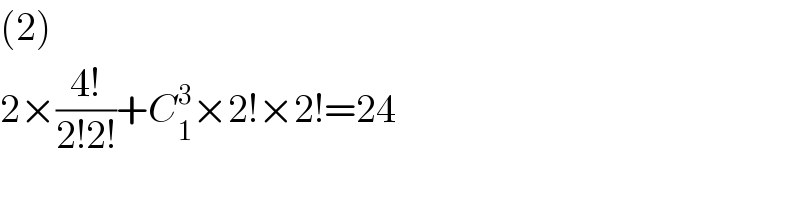
(2) 2×((4!)/(2!2!))+C_1 ^3 ×2!×2!=24
$$\left(\mathrm{2}\right) \\ $$$$\mathrm{2}×\frac{\mathrm{4}!}{\mathrm{2}!\mathrm{2}!}+{C}_{\mathrm{1}} ^{\mathrm{3}} ×\mathrm{2}!×\mathrm{2}!=\mathrm{24} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *