Question Number 115604 by bemath last updated on 27/Sep/20

$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{tan}\:{x}}\:=? \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}\:+\mathrm{cos}\:{x}}\:−\mathrm{1}}{\left(\pi−{x}\right)^{\mathrm{2}} }\:=\:? \\ $$
Commented by Dwaipayan Shikari last updated on 27/Sep/20
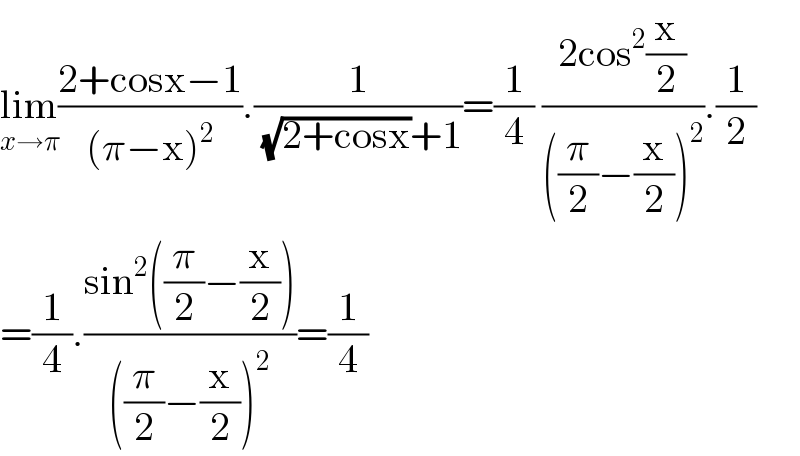
$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{\mathrm{2}+\mathrm{cosx}−\mathrm{1}}{\left(\pi−\mathrm{x}\right)^{\mathrm{2}} }.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}+\mathrm{cosx}}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\mathrm{2cos}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}{\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} }.\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\right)}{\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by bobhans last updated on 27/Sep/20

$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\frac{−\mathrm{sin}\:{x}}{\mathrm{2}\sqrt{\mathrm{2}+\mathrm{cos}\:{x}}}}{−\mathrm{2}\left(\pi−{x}\right)}\:=\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}+\mathrm{cos}\:{x}}}\:×\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}}{\pi−{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}×\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}}{−\mathrm{1}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}×\left(−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by Olaf last updated on 27/Sep/20

$$\left(\mathrm{2}\right) \\ $$$${x}\:=\:\pi−{u} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{2}−\mathrm{cos}{u}}−\mathrm{1}}{{u}^{\mathrm{2}} } \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{2}−\left(\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right)}−\mathrm{1}}{{u}^{\mathrm{2}} } \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+\frac{{u}^{\mathrm{2}} }{\mathrm{2}}}−\mathrm{1}}{{u}^{\mathrm{2}} } \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\frac{{u}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}}{{u}^{\mathrm{2}} } \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{u}^{\mathrm{2}} }{\mathrm{4}}}{{u}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 27/Sep/20

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{tanx}}\:\:\mathrm{changement}\:\mathrm{t}\:=\mathrm{x}−\frac{\pi}{\mathrm{2}}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{cos}\left(\mathrm{2}\left(\mathrm{t}+\frac{\pi}{\mathrm{2}}\right)\right)}{\mathrm{tan}\left(\mathrm{t}+\frac{\pi}{\mathrm{2}}\right)}\:=−\frac{\mathrm{cos}\left(\mathrm{2t}\right)}{−\frac{\mathrm{1}}{\mathrm{tant}}}\:=\mathrm{tant}\:.\mathrm{cos}\left(\mathrm{2t}\right) \\ $$$$\left(\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{t}\:\rightarrow\mathrm{0}\right)\:\Rightarrow\mathrm{tan}\left(\mathrm{t}\right)\sim\mathrm{t}\:\:\mathrm{and}\:\mathrm{cos}\left(\mathrm{2t}\right)\:\sim\mathrm{1}−\mathrm{2t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{tant}.\mathrm{cos}\left(\mathrm{2t}\right)\sim\mathrm{t}\left(\mathrm{1}−\mathrm{2t}^{\mathrm{2}} \right)\rightarrow\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 27/Sep/20

$$\left.\mathrm{2}\right)\:\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{2}+\mathrm{cosx}}−\mathrm{1}}{\left(\pi−\mathrm{x}\right)^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\pi−\mathrm{x}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{g}\left(\pi−\mathrm{t}\right)\:=\frac{\sqrt{\mathrm{2}+\mathrm{cos}\left(\pi−\mathrm{t}\right)}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\:=\frac{\sqrt{\mathrm{2}−\mathrm{cost}}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{cost}\:\sim\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow−\mathrm{cost}\:\sim−\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{2}−\mathrm{cost}\:\sim\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\mathrm{2}−\mathrm{cost}}\sim\sqrt{\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}}\sim\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow\mathrm{g}\left(\pi−\mathrm{t}\right)\sim\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4t}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \:\:\mathrm{g}\left(\pi−\mathrm{t}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\pi} \:\:\mathrm{g}\left(\mathrm{x}\right) \\ $$
Answered by bobhans last updated on 27/Sep/20

$$\left(\mathrm{1}\right)\:{set}\:{x}\:=\:{z}+\frac{\pi}{\mathrm{2}} \\ $$$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\left(\mathrm{2}{z}+\pi\right)}{\mathrm{tan}\:\left({z}+\frac{\pi}{\mathrm{2}}\right)}\:=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{cos}\:\mathrm{2}{z}}{−\mathrm{cot}\:{z}} \\ $$$$=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{tan}\:{z}.\:\mathrm{cos}\:\mathrm{2}{z}\:=\:\mathrm{0}.\: \\ $$
Answered by Olaf last updated on 27/Sep/20

$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\mathrm{cos2}{x}\:=\:−\mathrm{1} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\mathrm{tan}{x}\:=\:\pm\infty \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\mathrm{cos2}{x}}{\mathrm{tan}{x}}\:=\:\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
