Question Number 147093 by liberty last updated on 18/Jul/21
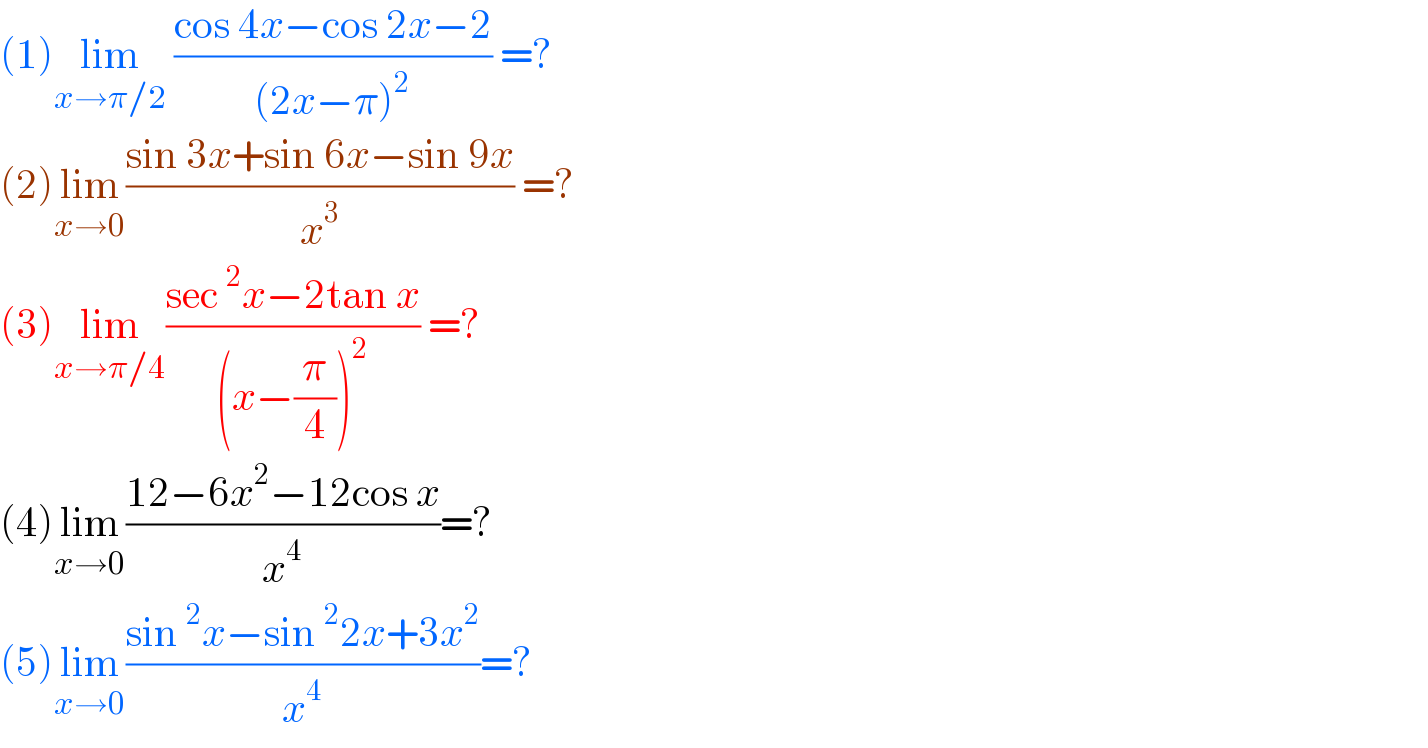
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{4}{x}−\mathrm{cos}\:\mathrm{2}{x}−\mathrm{2}}{\left(\mathrm{2}{x}−\pi\right)^{\mathrm{2}} }\:=? \\ $$$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{3}{x}+\mathrm{sin}\:\mathrm{6}{x}−\mathrm{sin}\:\mathrm{9}{x}}{{x}^{\mathrm{3}} }\:=? \\ $$$$\left(\mathrm{3}\right)\underset{{x}\rightarrow\pi/\mathrm{4}} {\mathrm{lim}}\frac{\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{2tan}\:{x}}{\left({x}−\frac{\pi}{\mathrm{4}}\right)^{\mathrm{2}} }\:=? \\ $$$$\left(\mathrm{4}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{12}−\mathrm{6}{x}^{\mathrm{2}} −\mathrm{12cos}\:{x}}{{x}^{\mathrm{4}} }=? \\ $$$$\left(\mathrm{5}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} }=? \\ $$
Commented by mathmax by abdo last updated on 18/Jul/21
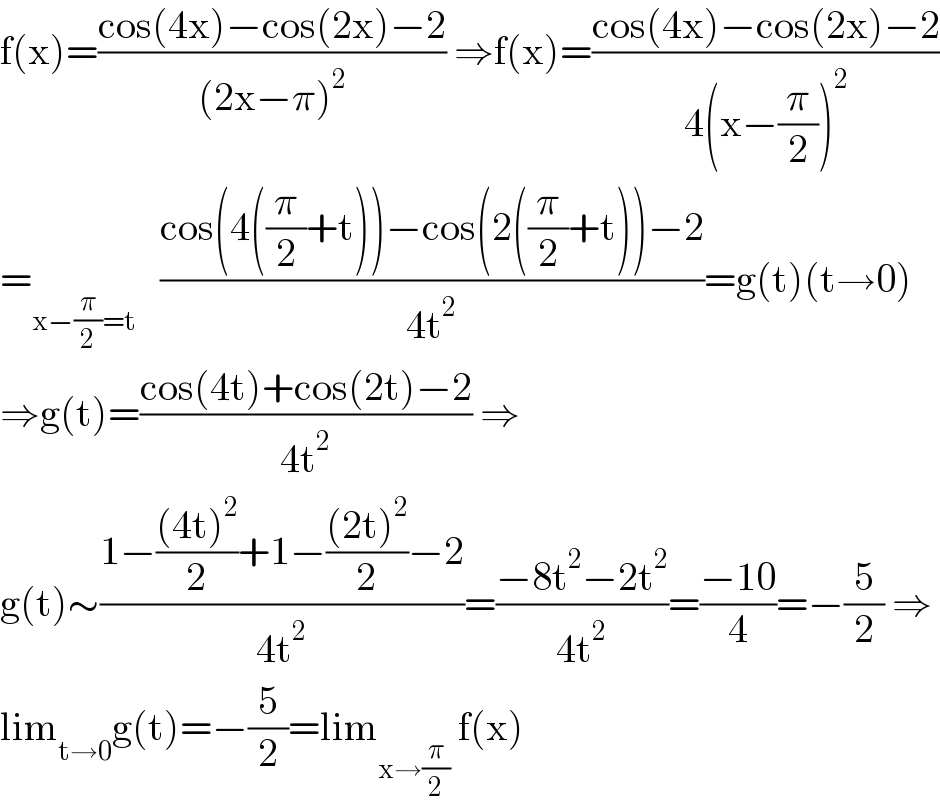
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{cos}\left(\mathrm{4x}\right)−\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{2}}{\left(\mathrm{2x}−\pi\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{cos}\left(\mathrm{4x}\right)−\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{2}}{\mathrm{4}\left(\mathrm{x}−\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=_{\mathrm{x}−\frac{\pi}{\mathrm{2}}=\mathrm{t}} \:\:\:\frac{\mathrm{cos}\left(\mathrm{4}\left(\frac{\pi}{\mathrm{2}}+\mathrm{t}\right)\right)−\mathrm{cos}\left(\mathrm{2}\left(\frac{\pi}{\mathrm{2}}+\mathrm{t}\right)\right)−\mathrm{2}}{\mathrm{4t}^{\mathrm{2}} }=\mathrm{g}\left(\mathrm{t}\right)\left(\mathrm{t}\rightarrow\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{t}\right)=\frac{\mathrm{cos}\left(\mathrm{4t}\right)+\mathrm{cos}\left(\mathrm{2t}\right)−\mathrm{2}}{\mathrm{4t}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{t}\right)\sim\frac{\mathrm{1}−\frac{\left(\mathrm{4t}\right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{1}−\frac{\left(\mathrm{2t}\right)^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}}{\mathrm{4t}^{\mathrm{2}} }=\frac{−\mathrm{8t}^{\mathrm{2}} −\mathrm{2t}^{\mathrm{2}} }{\mathrm{4t}^{\mathrm{2}} }=\frac{−\mathrm{10}}{\mathrm{4}}=−\frac{\mathrm{5}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{t}\right)=−\frac{\mathrm{5}}{\mathrm{2}}=\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\mathrm{f}\left(\mathrm{x}\right) \\ $$
Commented by liberty last updated on 18/Jul/21
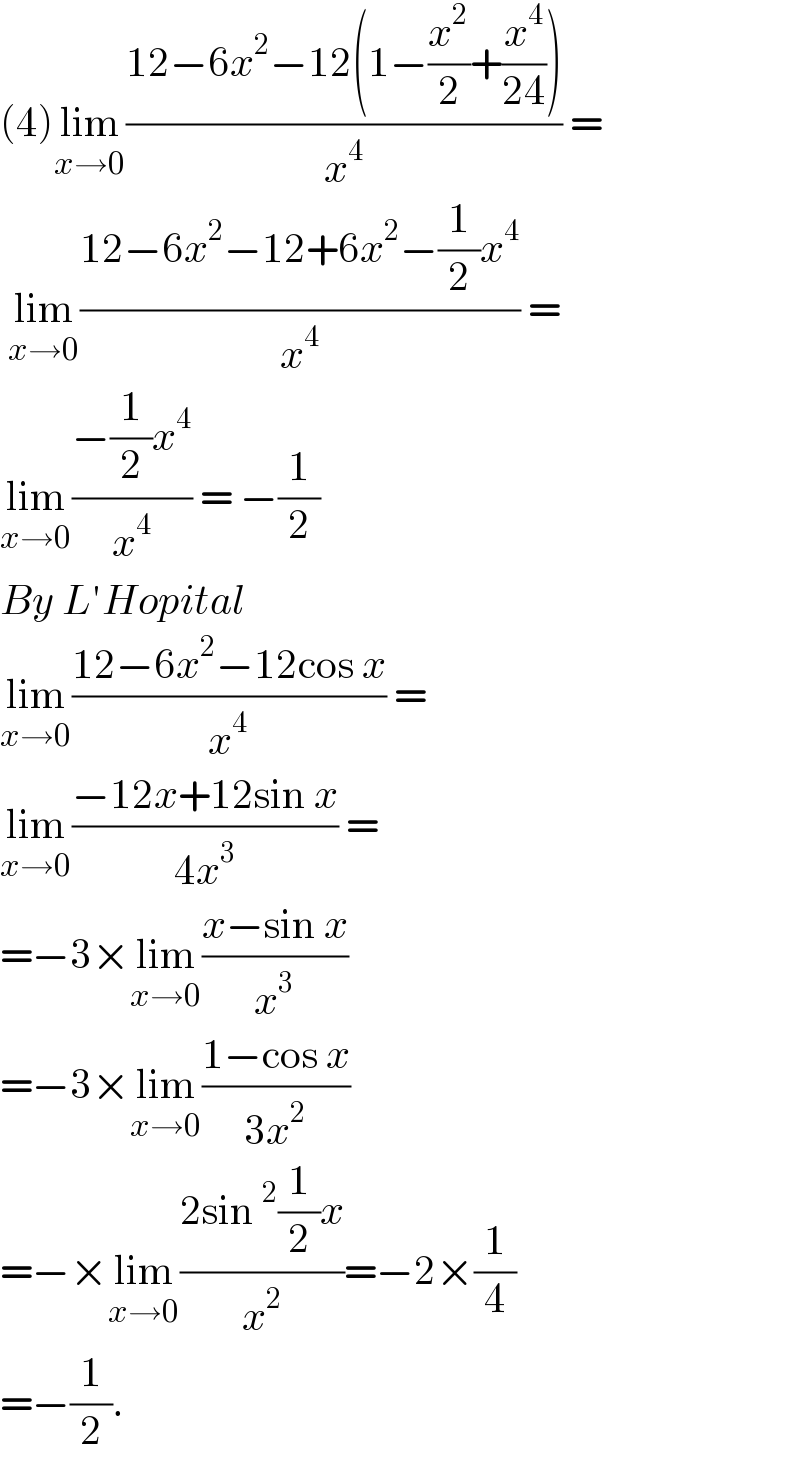
$$\left(\mathrm{4}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{12}−\mathrm{6}{x}^{\mathrm{2}} −\mathrm{12}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{4}} }{\mathrm{24}}\right)}{{x}^{\mathrm{4}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{12}−\mathrm{6}{x}^{\mathrm{2}} −\mathrm{12}+\mathrm{6}{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} }{{x}^{\mathrm{4}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} }{{x}^{\mathrm{4}} }\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${By}\:{L}'{Hopital}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{12}−\mathrm{6}{x}^{\mathrm{2}} −\mathrm{12cos}\:{x}}{{x}^{\mathrm{4}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{12}{x}+\mathrm{12sin}\:{x}}{\mathrm{4}{x}^{\mathrm{3}} }\:= \\ $$$$=−\mathrm{3}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{3}} }\: \\ $$$$=−\mathrm{3}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$=−×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}{x}}{{x}^{\mathrm{2}} }=−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}.\: \\ $$
Answered by EDWIN88 last updated on 18/Jul/21
![(1) lim_(x→(π/2)) ((cos 4x−cos 2x−2)/((2x−π)^2 ))=? sol : let x−(π/2)= t ; x=(π/2)+t lim_(t→0) ((cos (2π+4t)−cos (π+2t)−2)/(4t^2 )) = lim_(t→0) ((cos 4t+cos 2t−2)/(4t^2 )) = lim_(t→0) (((cos 4t−1)+(cos 2t−1))/(4t^2 )) = lim_(t→0) ((−2sin^2 2t−2sin^2 t)/(4t^2 )) =−(1/2)[lim_(t→0) (((sin 2t)/t))^2 +lim_(t→0) (((sin t)/t))^2 ] =−(1/2)(2^2 +1^2 )=−(5/2)](https://www.tinkutara.com/question/Q147095.png)
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\frac{\mathrm{cos}\:\mathrm{4x}−\mathrm{cos}\:\mathrm{2x}−\mathrm{2}}{\left(\mathrm{2x}−\pi\right)^{\mathrm{2}} }=? \\ $$$$\mathrm{sol}\::\:\mathrm{let}\:\mathrm{x}−\frac{\pi}{\mathrm{2}}=\:\mathrm{t}\:;\:\mathrm{x}=\frac{\pi}{\mathrm{2}}+\mathrm{t} \\ $$$$\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\left(\mathrm{2}\pi+\mathrm{4t}\right)−\mathrm{cos}\:\left(\pi+\mathrm{2t}\right)−\mathrm{2}}{\mathrm{4t}^{\mathrm{2}} } \\ $$$$=\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\mathrm{4t}+\mathrm{cos}\:\mathrm{2t}−\mathrm{2}}{\mathrm{4t}^{\mathrm{2}} } \\ $$$$=\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{cos}\:\mathrm{4t}−\mathrm{1}\right)+\left(\mathrm{cos}\:\mathrm{2t}−\mathrm{1}\right)}{\mathrm{4t}^{\mathrm{2}} } \\ $$$$=\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2t}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{t}}{\mathrm{4t}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\mathrm{2t}}{\mathrm{t}}\right)^{\mathrm{2}} +\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\mathrm{t}}{\mathrm{t}}\right)^{\mathrm{2}} \right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} \right)=−\frac{\mathrm{5}}{\mathrm{2}}\: \\ $$
Answered by EDWIN88 last updated on 18/Jul/21
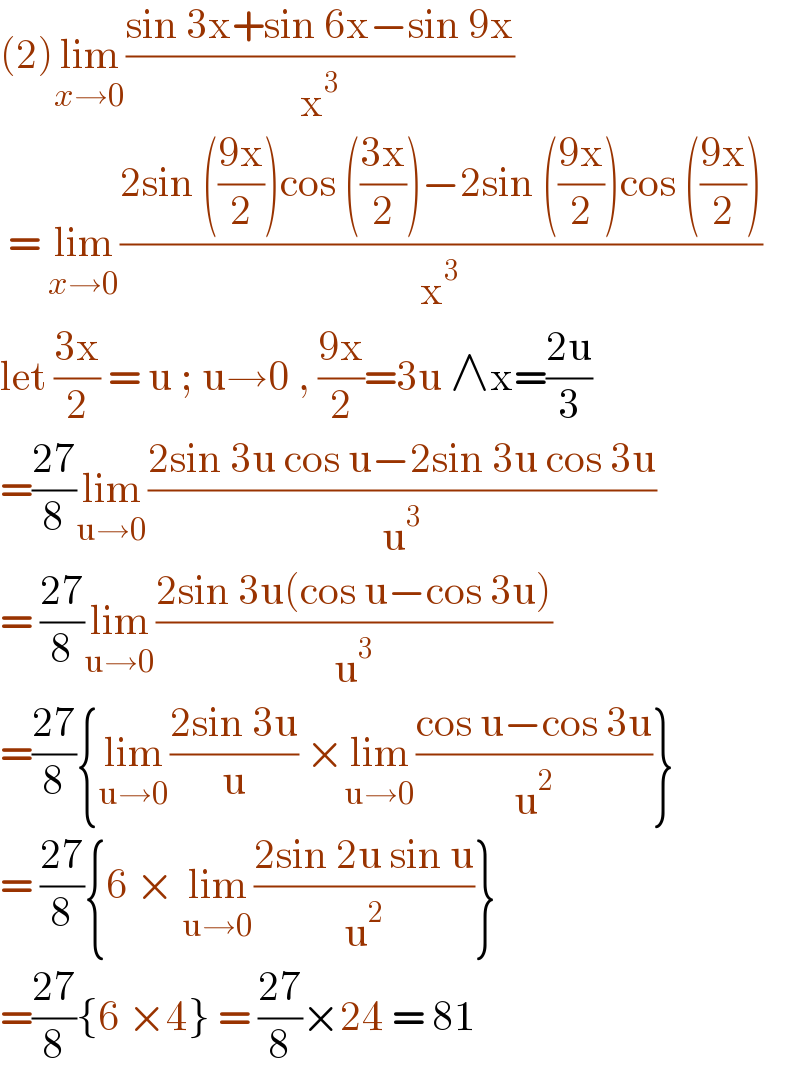
$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{3x}+\mathrm{sin}\:\mathrm{6x}−\mathrm{sin}\:\mathrm{9x}}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:\left(\frac{\mathrm{9x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{3x}}{\mathrm{2}}\right)−\mathrm{2sin}\:\left(\frac{\mathrm{9x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{9x}}{\mathrm{2}}\right)}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\mathrm{let}\:\frac{\mathrm{3x}}{\mathrm{2}}\:=\:\mathrm{u}\:;\:\mathrm{u}\rightarrow\mathrm{0}\:,\:\frac{\mathrm{9x}}{\mathrm{2}}=\mathrm{3u}\:\wedge\mathrm{x}=\frac{\mathrm{2u}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{27}}{\mathrm{8}}\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:\mathrm{3u}\:\mathrm{cos}\:\mathrm{u}−\mathrm{2sin}\:\mathrm{3u}\:\mathrm{cos}\:\mathrm{3u}}{\mathrm{u}^{\mathrm{3}} } \\ $$$$=\:\frac{\mathrm{27}}{\mathrm{8}}\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:\mathrm{3u}\left(\mathrm{cos}\:\mathrm{u}−\mathrm{cos}\:\mathrm{3u}\right)}{\mathrm{u}^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{27}}{\mathrm{8}}\left\{\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:\mathrm{3u}}{\mathrm{u}}\:×\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\mathrm{u}−\mathrm{cos}\:\mathrm{3u}}{\mathrm{u}^{\mathrm{2}} }\right\} \\ $$$$=\:\frac{\mathrm{27}}{\mathrm{8}}\left\{\mathrm{6}\:×\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:\mathrm{2u}\:\mathrm{sin}\:\mathrm{u}}{\mathrm{u}^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{27}}{\mathrm{8}}\left\{\mathrm{6}\:×\mathrm{4}\right\}\:=\:\frac{\mathrm{27}}{\mathrm{8}}×\mathrm{24}\:=\:\mathrm{81} \\ $$
Answered by liberty last updated on 18/Jul/21
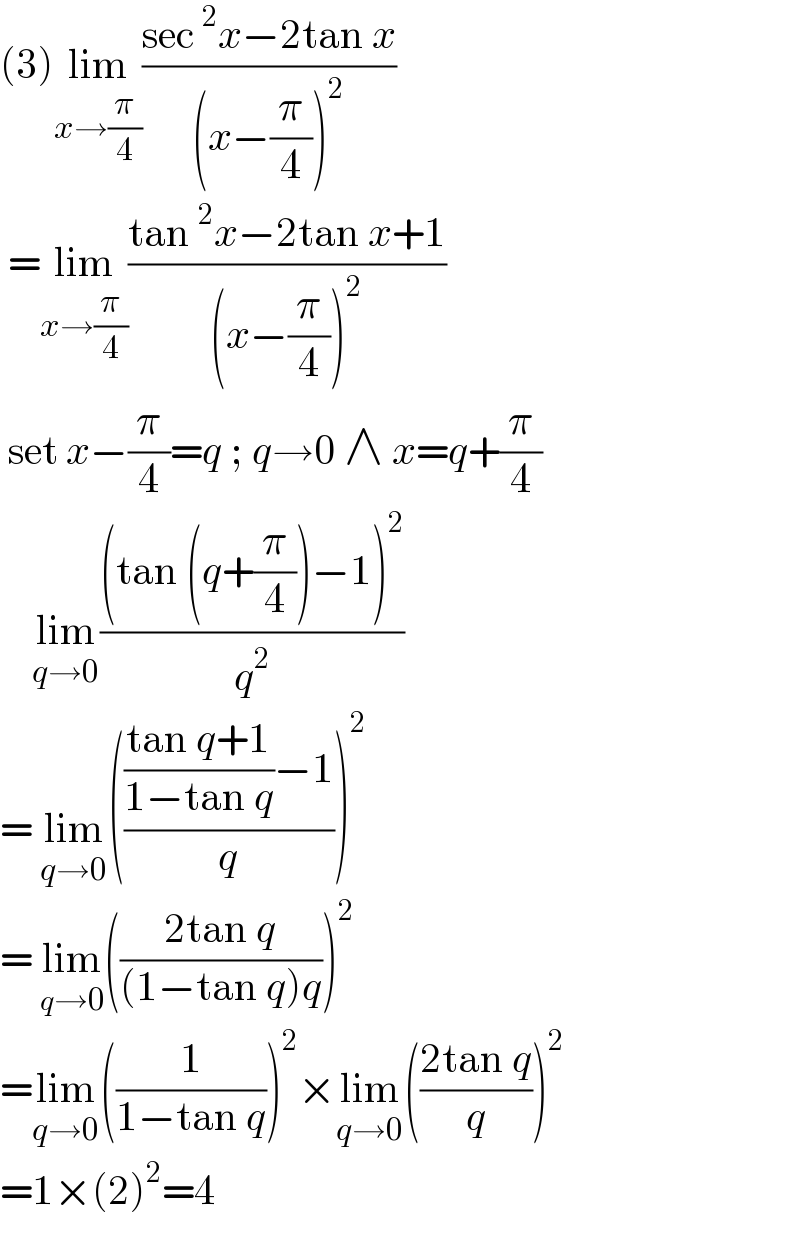
$$\left(\mathrm{3}\right)\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{2tan}\:{x}}{\left({x}−\frac{\pi}{\mathrm{4}}\right)^{\mathrm{2}} }\: \\ $$$$\:=\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\mathrm{tan}\:^{\mathrm{2}} {x}−\mathrm{2tan}\:{x}+\mathrm{1}}{\left({x}−\frac{\pi}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$\:\mathrm{set}\:{x}−\frac{\pi}{\mathrm{4}}={q}\:;\:{q}\rightarrow\mathrm{0}\:\wedge\:{x}={q}+\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{tan}\:\left({q}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{1}\right)^{\mathrm{2}} }{{q}^{\mathrm{2}} } \\ $$$$=\:\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\frac{\mathrm{tan}\:{q}+\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:{q}}−\mathrm{1}}{{q}}\right)^{\mathrm{2}} \\ $$$$=\:\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2tan}\:{q}}{\left(\mathrm{1}−\mathrm{tan}\:{q}\right){q}}\right)^{\mathrm{2}} \\ $$$$=\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:{q}}\right)^{\mathrm{2}} ×\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2tan}\:{q}}{{q}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{1}×\left(\mathrm{2}\right)^{\mathrm{2}} =\mathrm{4} \\ $$
