Question Number 125282 by Mammadli last updated on 09/Dec/20
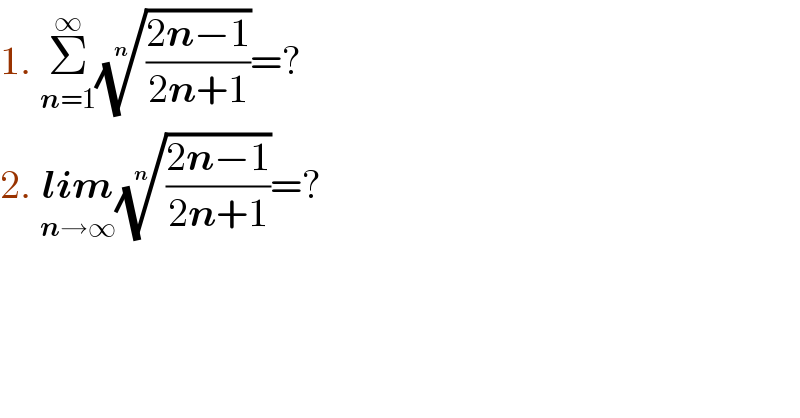
$$\mathrm{1}.\:\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\sqrt[{\boldsymbol{{n}}}]{\frac{\mathrm{2}\boldsymbol{{n}}−\mathrm{1}}{\mathrm{2}\boldsymbol{{n}}+\mathrm{1}}}=? \\ $$$$\mathrm{2}.\:\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{lim}}}\sqrt[{\boldsymbol{{n}}}]{\frac{\mathrm{2}\boldsymbol{{n}}−\mathrm{1}}{\mathrm{2}\boldsymbol{{n}}+\mathrm{1}}}=? \\ $$
Answered by mathmax by abdo last updated on 09/Dec/20
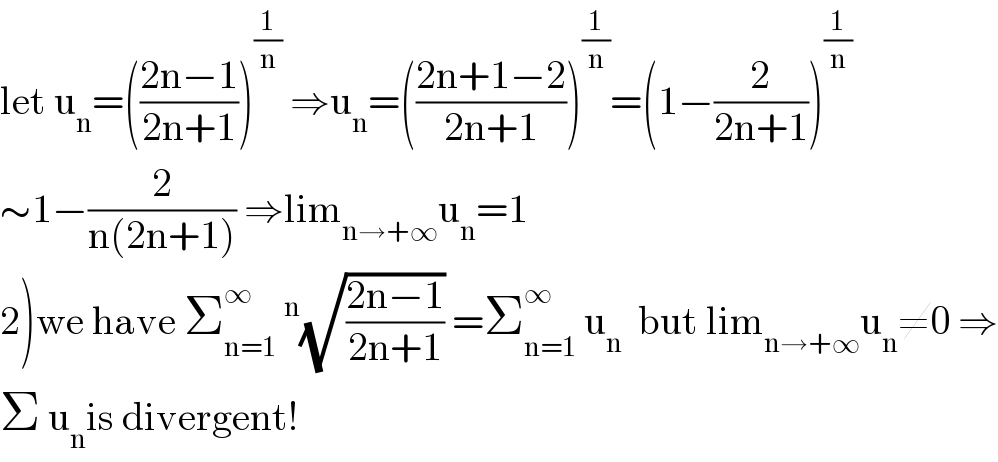
$$\mathrm{let}\:\mathrm{u}_{\mathrm{n}} =\left(\frac{\mathrm{2n}−\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:\Rightarrow\mathrm{u}_{\mathrm{n}} =\left(\frac{\mathrm{2n}+\mathrm{1}−\mathrm{2}}{\mathrm{2n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} =\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{2n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$\sim\mathrm{1}−\frac{\mathrm{2}}{\mathrm{n}\left(\mathrm{2n}+\mathrm{1}\right)}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} =\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:^{\mathrm{n}} \sqrt{\frac{\mathrm{2n}−\mathrm{1}}{\mathrm{2n}+\mathrm{1}}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{u}_{\mathrm{n}} \:\:\mathrm{but}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} \neq\mathrm{0}\:\Rightarrow \\ $$$$\Sigma\:\mathrm{u}_{\mathrm{n}} \mathrm{is}\:\mathrm{divergent}! \\ $$
Answered by Dwaipayan Shikari last updated on 09/Dec/20
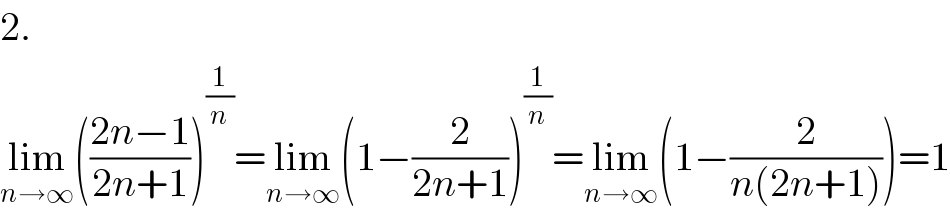
$$\mathrm{2}. \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{{n}}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{{n}}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{2}}{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)}\right)=\mathrm{1} \\ $$
