Question Number 101791 by Dwaipayan Shikari last updated on 04/Jul/20
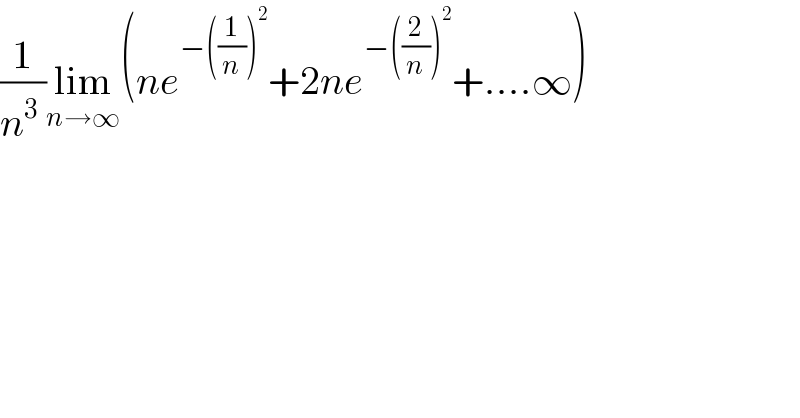
$$\frac{\mathrm{1}}{{n}^{\mathrm{3}\:\:} }\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left({ne}^{−\left(\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} } +\mathrm{2}{ne}^{−\left(\frac{\mathrm{2}}{{n}}\right)^{\mathrm{2}} } +….\infty\right) \\ $$
Answered by Ar Brandon last updated on 04/Jul/20
![lim_(n→∞) (1/n^3 ){ne^(−((1/n))^2 ) +2ne^(−((2/n))^2 ) +∙∙∙+n∙ne^(−((n/n))^2 ) } A_n =lim_(n→∞) (1/n^3 )Σ_(k=1) ^n {kne_ ^(−((k/n))^2 ) }=lim_(n→∞) (1/n)Σ_(k=1) ^n {(k/n)e^(−((k/n))^2 ) } =∫_0 ^1 xe^(−x^2 ) dx=(1/(−2))[e^(−x^2 ) ]_0 ^1 =(1/2){1−(1/e)}](https://www.tinkutara.com/question/Q101801.png)
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\left\{\mathrm{ne}^{−\left(\frac{\mathrm{1}}{\mathrm{n}}\right)^{\mathrm{2}} } +\mathrm{2ne}^{−\left(\frac{\mathrm{2}}{\mathrm{n}}\right)^{\mathrm{2}} } +\centerdot\centerdot\centerdot+\mathrm{n}\centerdot\mathrm{ne}^{−\left(\frac{\mathrm{n}}{\mathrm{n}}\right)^{\mathrm{2}} } \right\} \\ $$$$\mathrm{A}_{\mathrm{n}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left\{\mathrm{kne}_{} ^{−\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} } \right\}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left\{\frac{\mathrm{k}}{\mathrm{n}}\mathrm{e}^{−\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} } \right\} \\ $$$$\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}=\frac{\mathrm{1}}{−\mathrm{2}}\left[\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}}\right\} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 04/Jul/20
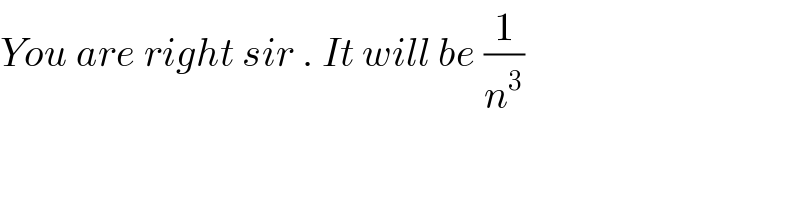
$${You}\:{are}\:{right}\:{sir}\:.\:{It}\:{will}\:{be}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$
Answered by mathmax by abdo last updated on 04/Jul/20
![A_n =(1/n^3 )Σ_(k=1) ^n nk e^(−(k^2 /(n^2 ))) ⇒ A_n =(1/n) Σ_(k=1) ^n (k/n)e^(−((k/n))^2 ) ⇒ lim_(n→+∞) A_n =∫_0 ^1 xe^(−x^2 ) dx =[−(1/2)e^(−x^2 ) ]_0 ^1 =(1/2) −(1/2)e^(−1) =(1/2)(1−(1/e)) =((e−1)/(2e))](https://www.tinkutara.com/question/Q101814.png)
$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{nk}\:\mathrm{e}^{−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} \:}} \:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{k}}{\mathrm{n}}\mathrm{e}^{−\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} } \:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}}\right) \\ $$$$=\frac{\mathrm{e}−\mathrm{1}}{\mathrm{2e}} \\ $$
Commented by Dwaipayan Shikari last updated on 04/Jul/20

$${Thanking}\:{you} \\ $$
Commented by mathmax by abdo last updated on 05/Jul/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
