Question Number 100539 by Dwaipayan Shikari last updated on 27/Jun/20
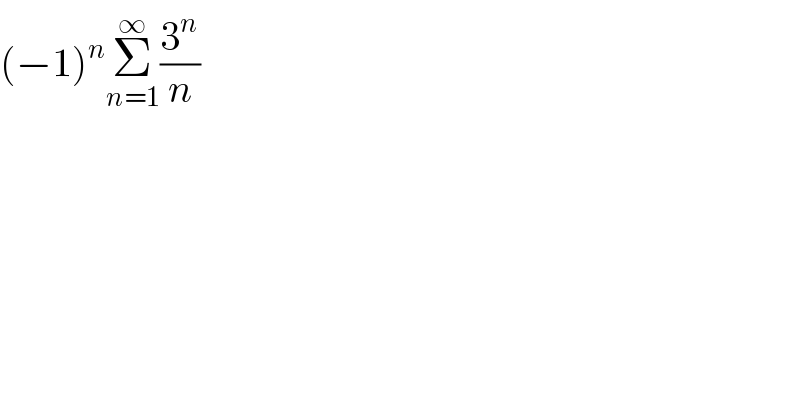
$$\left(−\mathrm{1}\right)^{{n}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3}^{{n}} }{{n}} \\ $$
Commented by maths mind last updated on 27/Jun/20
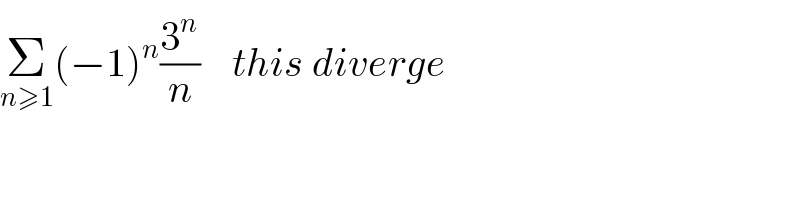
$$\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{3}^{{n}} }{{n}}\:\:\:\:{this}\:{diverge} \\ $$
Commented by abdomathmax last updated on 27/Jun/20

$$\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{u}_{\mathrm{n}} \:\:\mathrm{with}\:\mathrm{u}_{\mathrm{n}} =\frac{\left(−\mathrm{3}\right)^{\mathrm{n}} }{\mathrm{n}}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mid\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} }\mid\:=\frac{\mathrm{3}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}×\frac{\mathrm{n}}{\mathrm{3}^{\mathrm{n}} }\:=\frac{\mathrm{3n}}{\mathrm{n}+\mathrm{1}}\:\rightarrow\mathrm{3}\:>\mathrm{1}\:\Rightarrow\Sigma\:\mathrm{u}_{\mathrm{n}} \mathrm{diverges} \\ $$
