Question Number 147294 by ArielVyny last updated on 19/Jul/21
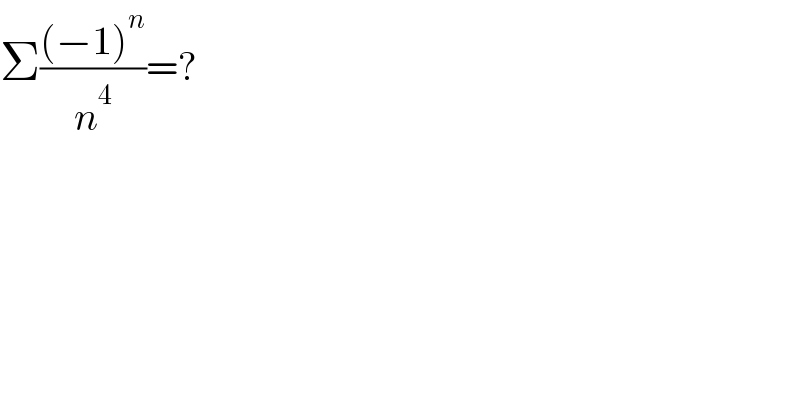
$$\Sigma\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{4}} }=? \\ $$
Answered by mathmax by abdo last updated on 19/Jul/21
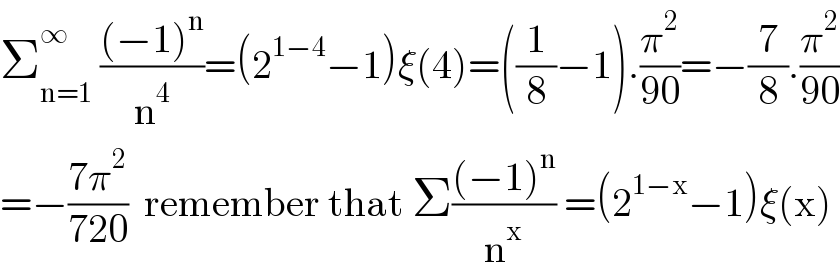
$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{4}} }=\left(\mathrm{2}^{\mathrm{1}−\mathrm{4}} −\mathrm{1}\right)\xi\left(\mathrm{4}\right)=\left(\frac{\mathrm{1}}{\mathrm{8}}−\mathrm{1}\right).\frac{\pi^{\mathrm{2}} }{\mathrm{90}}=−\frac{\mathrm{7}}{\mathrm{8}}.\frac{\pi^{\mathrm{2}} }{\mathrm{90}} \\ $$$$=−\frac{\mathrm{7}\pi^{\mathrm{2}} }{\mathrm{720}}\:\:\mathrm{remember}\:\mathrm{that}\:\Sigma\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{x}} }\:=\left(\mathrm{2}^{\mathrm{1}−\mathrm{x}} −\mathrm{1}\right)\xi\left(\mathrm{x}\right) \\ $$
Commented by ArielVyny last updated on 19/Jul/21

$$\xi\left(\mathrm{4}\right)=\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:{sir} \\ $$
Commented by ArielVyny last updated on 19/Jul/21
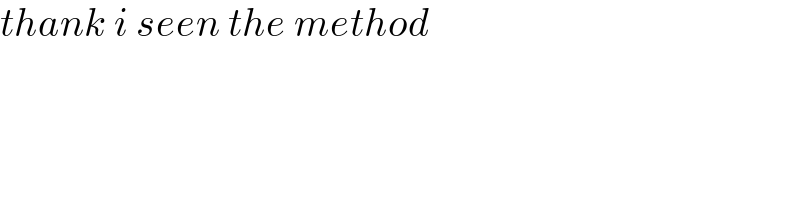
$${thank}\:{i}\:{seen}\:{the}\:{method} \\ $$
Commented by puissant last updated on 19/Jul/21

$${what}\:{is}\:{the}\:{name}\:{of}\:{the}\:{function}\:\xi\left({x}\right)..? \\ $$
Commented by ArielVyny last updated on 20/Jul/21

$${riemann} \\ $$
Commented by puissant last updated on 20/Jul/21
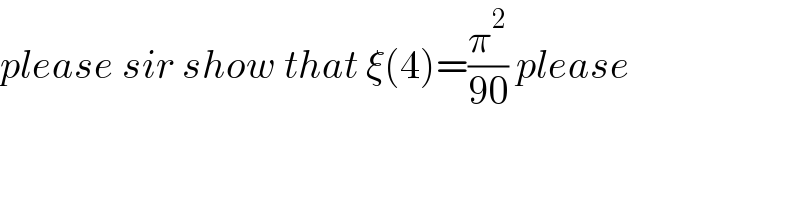
$${please}\:{sir}\:{show}\:{that}\:\xi\left(\mathrm{4}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{90}}\:{please} \\ $$
Commented by mathmax by abdo last updated on 20/Jul/21
$$\mathrm{zeta}\:\mathrm{Rieman}\:\mathrm{function} \\ $$
