Menu Close

1-n-n-n-1-2-n-n-1-n-2-3-n-n-1-n-2-n-3-4-

Tinku Tara 0 Comments
Pin




Question Number 37728 by kunal1234523 last updated on 17/Jun/18
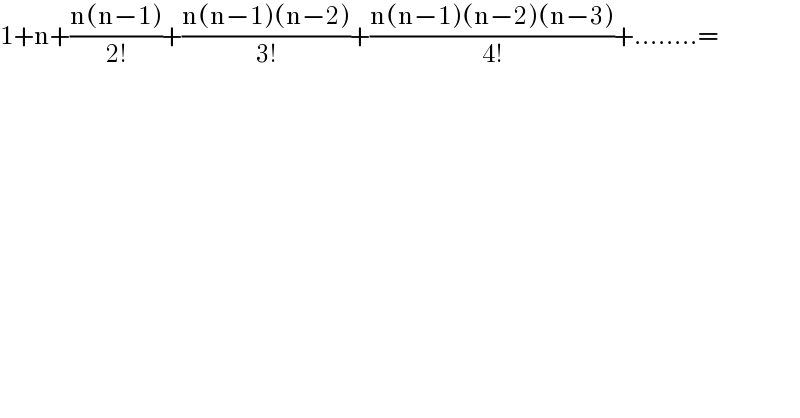
1+n+((n(n−1))/(2!))+((n(n−1)(n−2))/(3!))+((n(n−1)(n−2)(n−3))/(4!))+........=
$$\mathrm{1}+\mathrm{n}+\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{2}!}+\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)}{\mathrm{3}!}+\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\left(\mathrm{n}−\mathrm{3}\right)}{\mathrm{4}!}+……..= \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18
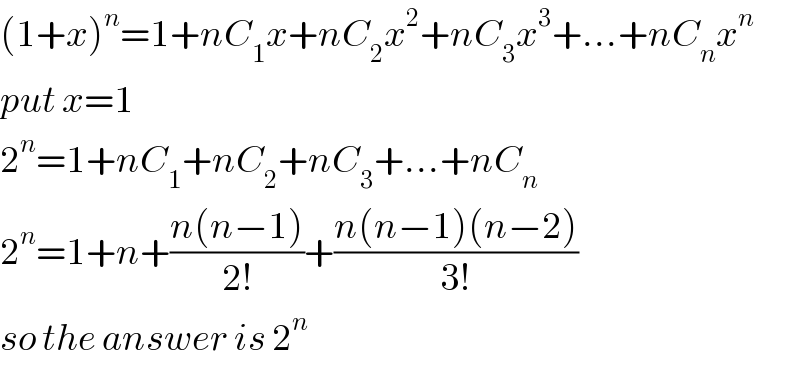
(1+x)^n =1+nC_1 x+nC_2 x^2 +nC_3 x^3 +...+nC_n x^n put x=1 2^n =1+nC_1 +nC_2 +nC_3 +...+nC_n 2^n =1+n+((n(n−1))/(2!))+((n(n−1)(n−2))/(3!)) so the answer is 2^n
$$\left(\mathrm{1}+{x}\right)^{{n}} =\mathrm{1}+{nC}_{\mathrm{1}} {x}+{nC}_{\mathrm{2}} {x}^{\mathrm{2}} +{nC}_{\mathrm{3}} {x}^{\mathrm{3}} +…+{nC}_{{n}} {x}^{{n}} \\ $$$${put}\:{x}=\mathrm{1} \\ $$$$\mathrm{2}^{{n}} =\mathrm{1}+{nC}_{\mathrm{1}} +{nC}_{\mathrm{2}} +{nC}_{\mathrm{3}} +…+{nC}_{{n}} \\ $$$$\mathrm{2}^{{n}} =\mathrm{1}+{n}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}+\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{3}!} \\ $$$${so}\:{the}\:{answer}\:{is}\:\mathrm{2}^{{n}} \\ $$
Commented by kunal1234523 last updated on 17/Jun/18
Commented by kunal1234523 last updated on 17/Jun/18
according to wolfram alpha it can not be determine in general form but you did it are you a genius
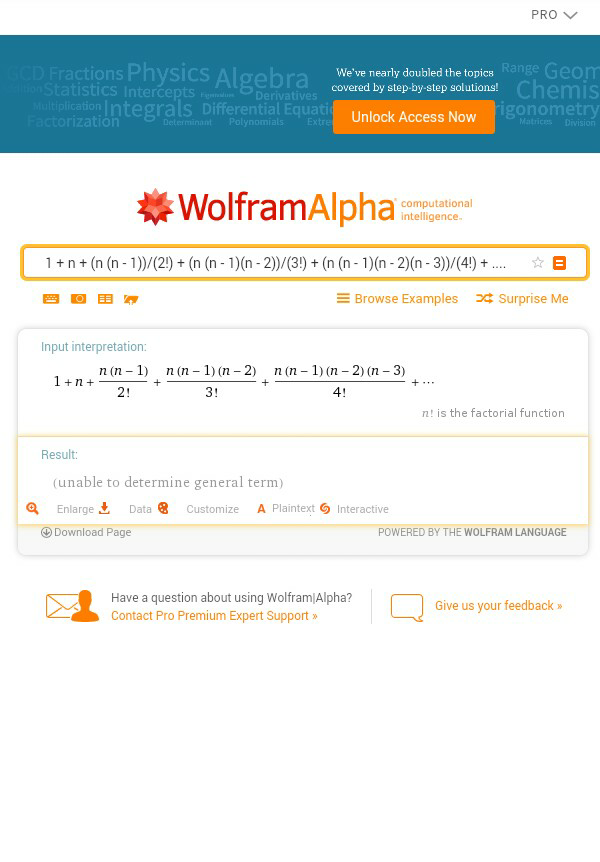
$$\mathrm{according}\:\mathrm{to}\:\mathrm{wolfram}\:\mathrm{alpha}\:\mathrm{it}\:\mathrm{can}\:\mathrm{not}\:\mathrm{be}\: \\ $$$$\mathrm{determine}\:\mathrm{in}\:\mathrm{general}\:\mathrm{form}\:\mathrm{but}\:\mathrm{you}\:\mathrm{did}\:\mathrm{it} \\ $$$$\mathrm{are}\:\mathrm{you}\:\mathrm{a}\:\mathrm{genius} \\ $$
Commented by kunal1234523 last updated on 17/Jun/18
This question is arived to me when I am working on sets. I came to know that no. of subsets of a set is 2^n where n is no.of terms or objects in the set. so I tried to prove it and I end up in the question that I had asked.
$$\mathrm{This}\:\mathrm{question}\:\mathrm{is}\:\mathrm{arived}\:\mathrm{to}\:\mathrm{me}\:\mathrm{when}\:\mathrm{I}\:\mathrm{am}\: \\ $$$$\mathrm{working}\:\mathrm{on}\:\mathrm{sets}.\:\mathrm{I}\:\mathrm{came}\:\mathrm{to}\:\mathrm{know}\:\mathrm{that}\:\mathrm{no}.\:\mathrm{of} \\ $$$$\mathrm{subsets}\:\mathrm{of}\:\:\mathrm{a}\:\mathrm{set}\:\mathrm{is}\:\mathrm{2}^{\mathrm{n}} \:\mathrm{where}\:\mathrm{n}\:\mathrm{is}\:\mathrm{no}.\mathrm{of}\:\mathrm{terms} \\ $$$$\mathrm{or}\:\mathrm{objects}\:\mathrm{in}\:\mathrm{the}\:\mathrm{set}.\:\mathrm{so}\:\mathrm{I}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{it}\:\mathrm{and} \\ $$$$\mathrm{I}\:\mathrm{end}\:\mathrm{up}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}\:\mathrm{that}\:\mathrm{I}\:\mathrm{had}\:\mathrm{asked}.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *