Question Number 128385 by n0y0n last updated on 06/Jan/21

$$\int_{\mathrm{1}} ^{\:\pi} \begin{vmatrix}{\mathrm{x}^{\mathrm{3}} }&{\mathrm{lnx}}&{\mathrm{sinx}}\\{\mathrm{3x}^{\mathrm{2}} }&{\frac{\mathrm{1}}{\mathrm{x}}}&{\mathrm{cosx}}\\{\mathrm{6}}&{\mathrm{2x}^{−\mathrm{3}} }&{−\mathrm{cosx}}\end{vmatrix}\mathrm{dx}\:=?\: \\ $$
Answered by mathmax by abdo last updated on 06/Jan/21
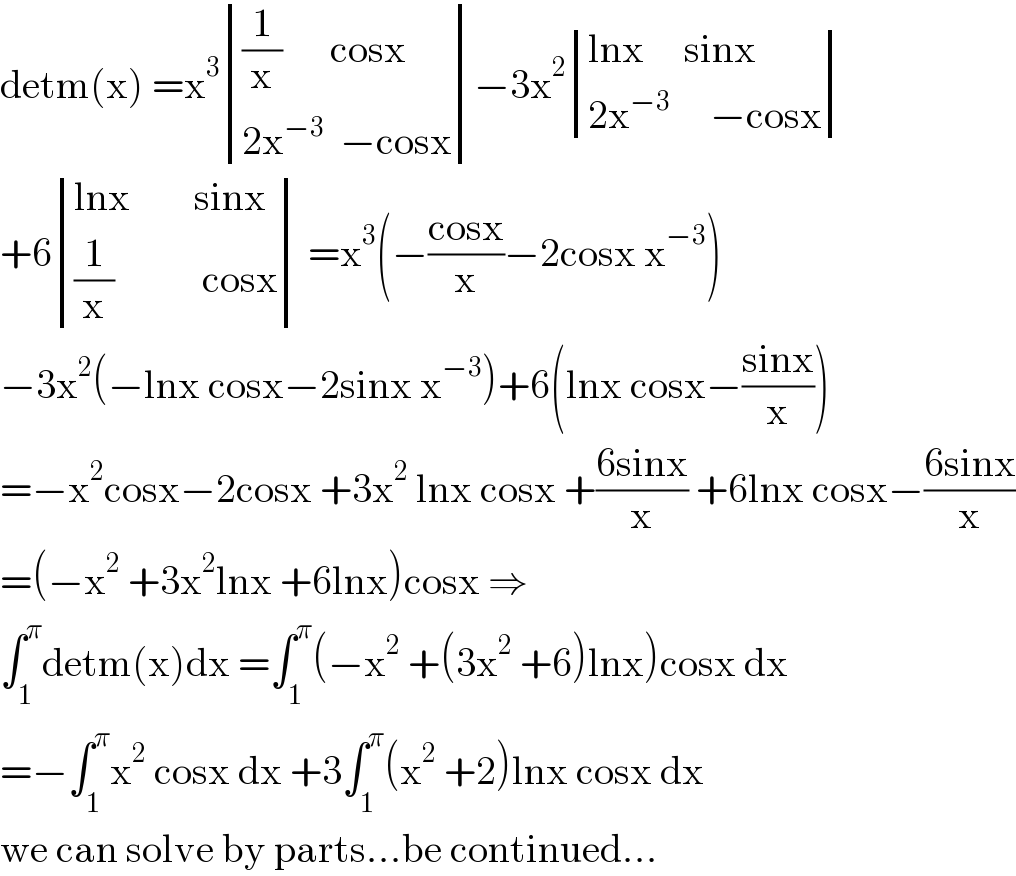
$$\mathrm{detm}\left(\mathrm{x}\right)\:=\mathrm{x}^{\mathrm{3}} \begin{vmatrix}{\frac{\mathrm{1}}{\mathrm{x}}\:\:\:\:\:\:\mathrm{cosx}}\\{\mathrm{2x}^{−\mathrm{3}} \:\:−\mathrm{cosx}}\end{vmatrix}−\mathrm{3x}^{\mathrm{2}} \begin{vmatrix}{\mathrm{lnx}\:\:\:\:\:\mathrm{sinx}}\\{\mathrm{2x}^{−\mathrm{3}} \:\:\:\:\:−\mathrm{cosx}}\end{vmatrix} \\ $$$$+\mathrm{6}\begin{vmatrix}{\mathrm{lnx}\:\:\:\:\:\:\:\:\mathrm{sinx}}\\{\frac{\mathrm{1}}{\mathrm{x}}\:\:\:\:\:\:\:\:\:\:\:\mathrm{cosx}}\end{vmatrix}\:=\mathrm{x}^{\mathrm{3}} \left(−\frac{\mathrm{cosx}}{\mathrm{x}}−\mathrm{2cosx}\:\mathrm{x}^{−\mathrm{3}} \right) \\ $$$$−\mathrm{3x}^{\mathrm{2}} \left(−\mathrm{lnx}\:\mathrm{cosx}−\mathrm{2sinx}\:\mathrm{x}^{−\mathrm{3}} \right)+\mathrm{6}\left(\mathrm{lnx}\:\mathrm{cosx}−\frac{\mathrm{sinx}}{\mathrm{x}}\right) \\ $$$$=−\mathrm{x}^{\mathrm{2}} \mathrm{cosx}−\mathrm{2cosx}\:+\mathrm{3x}^{\mathrm{2}} \:\mathrm{lnx}\:\mathrm{cosx}\:+\frac{\mathrm{6sinx}}{\mathrm{x}}\:+\mathrm{6lnx}\:\mathrm{cosx}−\frac{\mathrm{6sinx}}{\mathrm{x}} \\ $$$$=\left(−\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}^{\mathrm{2}} \mathrm{lnx}\:+\mathrm{6lnx}\right)\mathrm{cosx}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\pi} \mathrm{detm}\left(\mathrm{x}\right)\mathrm{dx}\:=\int_{\mathrm{1}} ^{\pi} \left(−\mathrm{x}^{\mathrm{2}} \:+\left(\mathrm{3x}^{\mathrm{2}} \:+\mathrm{6}\right)\mathrm{lnx}\right)\mathrm{cosx}\:\mathrm{dx} \\ $$$$=−\int_{\mathrm{1}} ^{\pi} \mathrm{x}^{\mathrm{2}} \:\mathrm{cosx}\:\mathrm{dx}\:+\mathrm{3}\int_{\mathrm{1}} ^{\pi} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\right)\mathrm{lnx}\:\mathrm{cosx}\:\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{parts}…\mathrm{be}\:\mathrm{continued}… \\ $$
