Question Number 122739 by mohammad17 last updated on 19/Nov/20
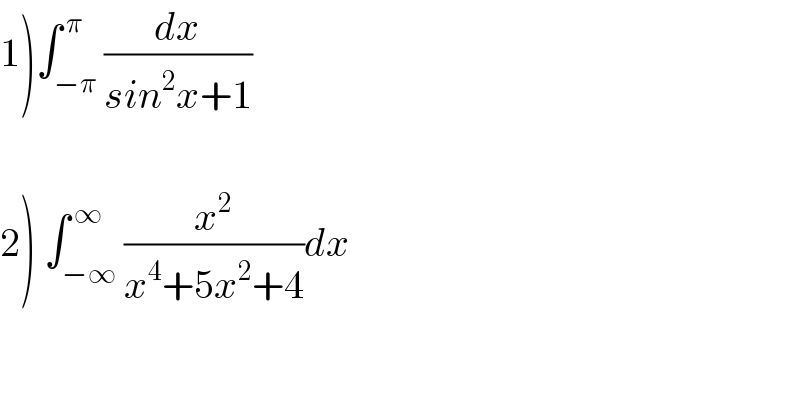
$$\left.\mathrm{1}\right)\int_{−\pi} ^{\:\pi} \frac{{dx}}{{sin}^{\mathrm{2}} {x}+\mathrm{1}} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:\int_{−\infty} ^{\:\infty} \frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 19/Nov/20
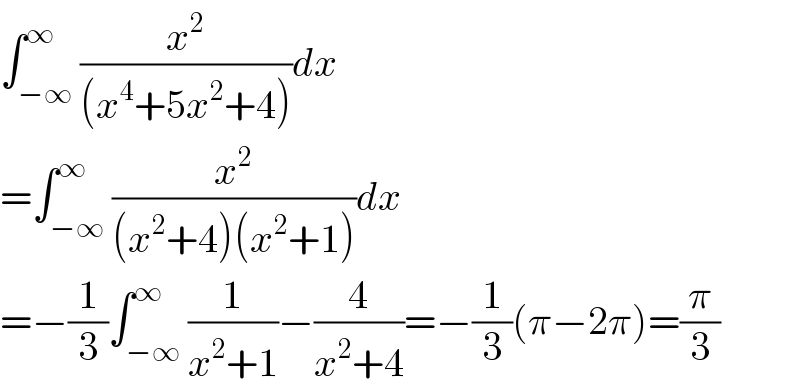
$$\int_{−\infty} ^{\infty} \frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}\right)}{dx} \\ $$$$=\int_{−\infty} ^{\infty} \frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{4}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\int_{−\infty} ^{\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{4}}{{x}^{\mathrm{2}} +\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{3}}\left(\pi−\mathrm{2}\pi\right)=\frac{\pi}{\mathrm{3}} \\ $$
Commented by mohammad17 last updated on 19/Nov/20

$${thank}\:{you}\:{mis} \\ $$
Answered by MJS_new last updated on 19/Nov/20
![∫(dx/(1+sin^2 x))= [t=tan x → dx=(dt/(t^2 +1))] =∫(dt/(2t^2 +1))=((√2)/2)arctan ((√2)t) = =((√2)/2)arctan ((√2)tan x) +C ∫_(−π) ^π (dx/(1+sin^2 x))=4∫_0 ^(π/2) (dx/(1+sin^2 x)) ⇒ answer is π(√2)](https://www.tinkutara.com/question/Q122742.png)
$$\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\int\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{t}\right)\:= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}\mathrm{tan}\:{x}\right)\:+{C} \\ $$$$\underset{−\pi} {\overset{\pi} {\int}}\frac{{dx}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:{x}}=\mathrm{4}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{dx}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:{x}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\pi\sqrt{\mathrm{2}} \\ $$
Commented by mohammad17 last updated on 19/Nov/20

$${put}\:{sir}\:{answer}\:\sqrt{\mathrm{2}\pi} \\ $$
Commented by MJS_new last updated on 19/Nov/20
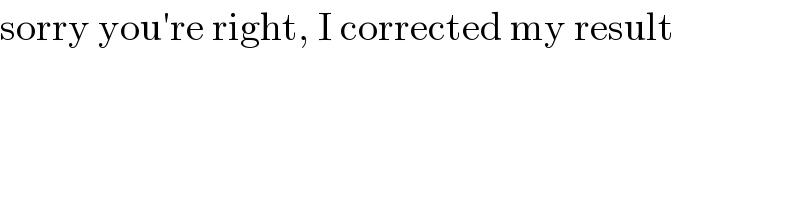
$$\mathrm{sorry}\:\mathrm{you}'\mathrm{re}\:\mathrm{right},\:\mathrm{I}\:\mathrm{corrected}\:\mathrm{my}\:\mathrm{result} \\ $$
Commented by mohammad17 last updated on 19/Nov/20

$${now}\:{its}\:{right} \\ $$
Answered by bemath last updated on 19/Nov/20
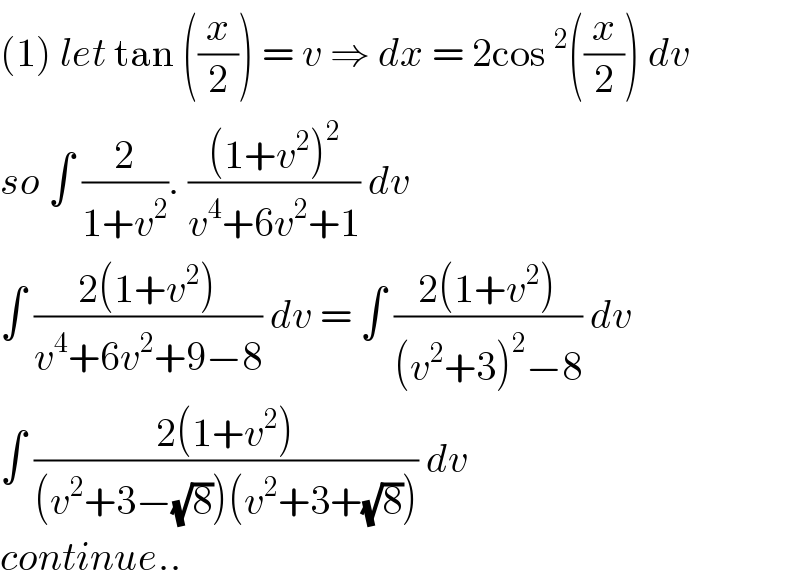
$$\left(\mathrm{1}\right)\:{let}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\:=\:{v}\:\Rightarrow\:{dx}\:=\:\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\:{dv}\: \\ $$$${so}\:\int\:\frac{\mathrm{2}}{\mathrm{1}+{v}^{\mathrm{2}} }.\:\frac{\left(\mathrm{1}+{v}^{\mathrm{2}} \right)^{\mathrm{2}} }{{v}^{\mathrm{4}} +\mathrm{6}{v}^{\mathrm{2}} +\mathrm{1}}\:{dv}\:\: \\ $$$$\int\:\frac{\mathrm{2}\left(\mathrm{1}+{v}^{\mathrm{2}} \right)}{{v}^{\mathrm{4}} +\mathrm{6}{v}^{\mathrm{2}} +\mathrm{9}−\mathrm{8}}\:{dv}\:=\:\int\:\frac{\mathrm{2}\left(\mathrm{1}+{v}^{\mathrm{2}} \right)}{\left({v}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} −\mathrm{8}}\:{dv} \\ $$$$\int\:\frac{\mathrm{2}\left(\mathrm{1}+{v}^{\mathrm{2}} \right)}{\left({v}^{\mathrm{2}} +\mathrm{3}−\sqrt{\mathrm{8}}\right)\left({v}^{\mathrm{2}} +\mathrm{3}+\sqrt{\mathrm{8}}\right)}\:{dv} \\ $$$${continue}.. \\ $$
Answered by Bird last updated on 19/Nov/20

$$\left.\mathrm{1}\right)\:{I}\:=\:\int_{−\pi} ^{\pi} \:\frac{{dx}}{{sin}^{\mathrm{2}} {x}\:+\mathrm{1}}\:\Rightarrow \\ $$$${I}\:=\int_{−\pi} ^{\pi} \:\frac{{dx}}{\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}+\mathrm{1}} \\ $$$$=\int_{−\pi} ^{\pi} \:\frac{\mathrm{2}{dx}}{\mathrm{3}−{cos}\left(\mathrm{2}{x}\right)} \\ $$$$=_{\mathrm{2}{x}={t}} \:\:\:\:\int_{−\mathrm{2}\pi} ^{\mathrm{2}\pi} \:\:\frac{{dt}}{\mathrm{3}−{cost}} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{dt}}{\mathrm{3}−{cost}} \\ $$$$=_{{z}={e}^{{it}} } \:\:\:\mathrm{2}\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\frac{{dz}}{{iz}\left(\mathrm{3}−\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}\right)} \\ $$$$=−\mathrm{4}{i}\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{{dz}}{{z}\left(\mathrm{6}−{z}−{z}^{−\mathrm{1}} \right)} \\ $$$$=−\mathrm{4}{i}\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{{dz}}{\mathrm{6}{z}−{z}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{4}{idz}}{{z}^{\mathrm{2}} −\mathrm{6}{z}+\mathrm{1}} \\ $$$$\varphi\left({z}\right)=\frac{\mathrm{4}{i}}{{z}^{\mathrm{2}} −\mathrm{6}{z}\:+\mathrm{1}} \\ $$$$\Delta^{'} \:=\mathrm{9}−\mathrm{1}=\mathrm{8}\:\Rightarrow{z}_{\mathrm{1}} =\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mathrm{z}_{\mathrm{2}} =\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\varphi\left({z}\right)\:=\frac{\mathrm{4}{i}}{\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)} \\ $$$$\mid{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\:=\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}>\mathrm{0} \\ $$$$\mid{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}=\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}<\mathrm{0} \\ $$$$\Rightarrow\int_{\mid{z}\mid=\mathrm{1}} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{2}} \right) \\ $$$$=\mathrm{2}{i}\pi×\frac{\mathrm{4}{i}}{\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)}\:=\frac{−\mathrm{8}\pi}{−\mathrm{4}\sqrt{\mathrm{2}}}\:=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}\pi\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\pi\sqrt{\mathrm{2}}\:\Rightarrow\:{I}\:=\pi\sqrt{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 20/Nov/20
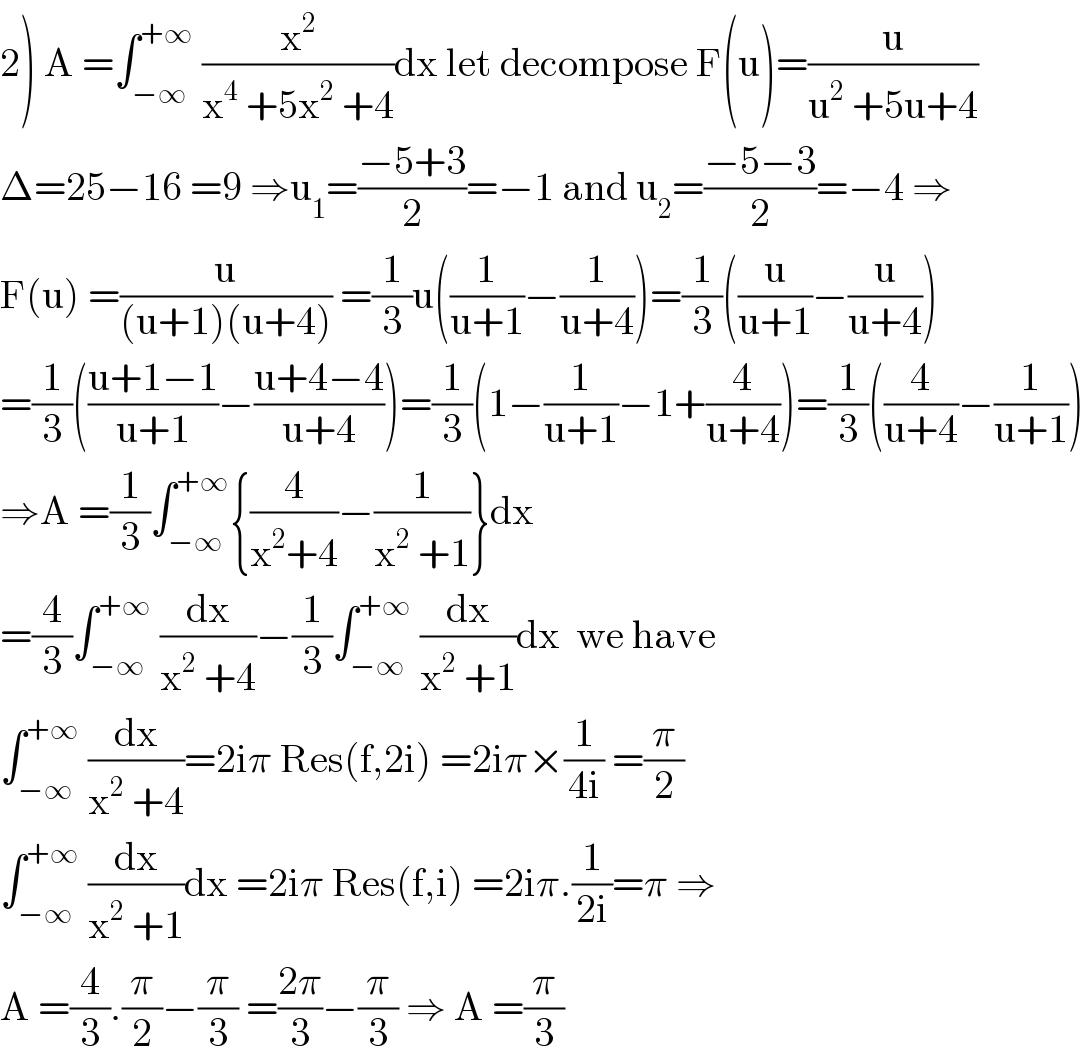
$$\left.\mathrm{2}\right)\:\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} \:+\mathrm{5x}^{\mathrm{2}} \:+\mathrm{4}}\mathrm{dx}\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{u}\right)=\frac{\mathrm{u}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{5u}+\mathrm{4}} \\ $$$$\Delta=\mathrm{25}−\mathrm{16}\:=\mathrm{9}\:\Rightarrow\mathrm{u}_{\mathrm{1}} =\frac{−\mathrm{5}+\mathrm{3}}{\mathrm{2}}=−\mathrm{1}\:\mathrm{and}\:\mathrm{u}_{\mathrm{2}} =\frac{−\mathrm{5}−\mathrm{3}}{\mathrm{2}}=−\mathrm{4}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{u}}{\left(\mathrm{u}+\mathrm{1}\right)\left(\mathrm{u}+\mathrm{4}\right)}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{u}\left(\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{u}}{\mathrm{u}+\mathrm{1}}−\frac{\mathrm{u}}{\mathrm{u}+\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{u}+\mathrm{1}−\mathrm{1}}{\mathrm{u}+\mathrm{1}}−\frac{\mathrm{u}+\mathrm{4}−\mathrm{4}}{\mathrm{u}+\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}−\mathrm{1}+\frac{\mathrm{4}}{\mathrm{u}+\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{4}}{\mathrm{u}+\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}\right) \\ $$$$\Rightarrow\mathrm{A}\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{−\infty} ^{+\infty} \left\{\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\right\}\mathrm{dx} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{3}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{f},\mathrm{2i}\right)\:=\mathrm{2i}\pi×\frac{\mathrm{1}}{\mathrm{4i}}\:=\frac{\pi}{\mathrm{2}} \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)\:=\mathrm{2i}\pi.\frac{\mathrm{1}}{\mathrm{2i}}=\pi\:\Rightarrow \\ $$$$\mathrm{A}\:=\frac{\mathrm{4}}{\mathrm{3}}.\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\:=\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{3}}\:\Rightarrow\:\mathrm{A}\:=\frac{\pi}{\mathrm{3}} \\ $$
