Question Number 185873 by test1234 last updated on 29/Jan/23

$$\left(\mathrm{1}\right)\:\int\pi{x}^{\mathrm{2}} +\sqrt{\frac{{xe}^{\pi} }{{x}^{\mathrm{2}} }}{dx}=? \\ $$$$\left(\mathrm{2}\right)\:\int\frac{\mathrm{ln}\:\left({x}\right)+\mathrm{ln}\:\left(\frac{−{z}}{{x}}\right)}{{x}^{{z}} }+{z}^{{x}} {dx}=? \\ $$
Answered by JDamian last updated on 29/Jan/23
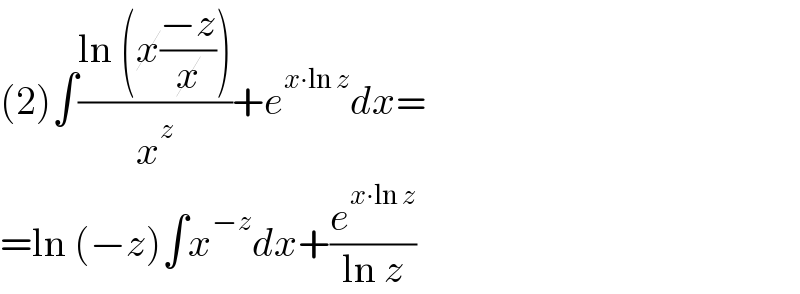
$$\left(\mathrm{2}\right)\int\frac{\mathrm{ln}\:\left(\cancel{{x}}\frac{−{z}}{\cancel{{x}}}\right)}{{x}^{{z}} }+{e}^{{x}\centerdot\mathrm{ln}\:{z}} {dx}= \\ $$$$=\mathrm{ln}\:\left(−{z}\right)\int{x}^{−{z}} {dx}+\frac{{e}^{{x}\centerdot\mathrm{ln}\:{z}} }{\mathrm{ln}\:{z}} \\ $$
Answered by aba last updated on 29/Jan/23

$$\left(\mathrm{1}\right)\int\pi\mathrm{x}^{\mathrm{2}} +\sqrt{\frac{\mathrm{xe}^{\pi} }{\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}=\int\left(\pi\mathrm{x}^{\mathrm{2}} +\sqrt{\mathrm{e}^{\pi} }.\mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\pi\mathrm{x}^{\mathrm{3}} +\mathrm{2}\sqrt{\mathrm{e}^{\pi} \mathrm{x}}+\mathrm{k} \\ $$
