Question Number 183943 by SulaymonNorboyev last updated on 31/Dec/22
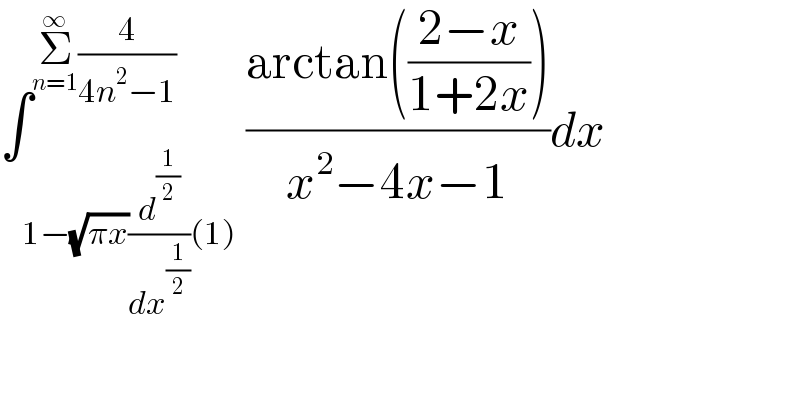
$$\int_{\mathrm{1}−\sqrt{\pi{x}}\frac{{d}^{\frac{\mathrm{1}}{\mathrm{2}}} }{{dx}^{\frac{\mathrm{1}}{\mathrm{2}}} }\left(\mathrm{1}\right)} ^{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}}{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}}\:} \frac{\mathrm{arctan}\left(\frac{\mathrm{2}−{x}}{\mathrm{1}+\mathrm{2}{x}}\right)}{{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{1}}{dx} \\ $$
Commented by SEKRET last updated on 02/Jan/23

$$\:\:\boldsymbol{\mathrm{sulaymon}}\:\:\boldsymbol{\mathrm{misolni}}\:\:\boldsymbol{\mathrm{tushuntirib}}\:\:\boldsymbol{\mathrm{yozing}} \\ $$$$\boldsymbol{\mathrm{tepadagi}}\:\boldsymbol{\mathrm{suma}}\:\:\mathrm{2}\:\:\boldsymbol{\mathrm{chiqadi}}\:\:\boldsymbol{\mathrm{integral}}\:\:\boldsymbol{\mathrm{olsa}} \\ $$$$\boldsymbol{\mathrm{boladi}}\:\boldsymbol{\mathrm{bolaklab}}\:\:\boldsymbol{\mathrm{integral}}\:\:\boldsymbol{\mathrm{pastidagi}}\:\boldsymbol{\mathrm{nima}}\:\boldsymbol{\mathrm{eknaligini}} \\ $$$$\boldsymbol{\mathrm{tushuntirib}}\:\boldsymbol{\mathrm{yozing}}\:\:\boldsymbol{\mathrm{qandaydir}}\:\:\boldsymbol{\mathrm{funksiyami}} \\ $$$$\boldsymbol{\mathrm{yoki}}\:\:\boldsymbol{\mathrm{oddiy}}\:\:\boldsymbol{\mathrm{xarflarmi}}. \\ $$
