Question Number 158945 by LEKOUMA last updated on 10/Nov/21

$$\left.\mathrm{1}\right)\:{Prove}\:{by}\:{absurd}\:{that}\: \\ $$$$\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{3}}\:\:{is}\:{irrational} \\ $$$$\left.\mathrm{2}\right)\:{Prove}\:{by}\:{absurd}\:{that} \\ $$$$\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}\:}\leqslant\sqrt{\mathrm{15}} \\ $$
Answered by mr W last updated on 10/Nov/21

$${say} \\ $$$$\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}\geqslant\sqrt{\mathrm{15}} \\ $$$$\mathrm{8}+\mathrm{4}\sqrt{\mathrm{3}}\geqslant\mathrm{15} \\ $$$$\mathrm{4}\sqrt{\mathrm{3}}\geqslant\mathrm{7} \\ $$$$\mathrm{16}×\mathrm{3}\geqslant\mathrm{49} \\ $$$$\mathrm{48}\geqslant\mathrm{49}\:\Rightarrow{contradiction}! \\ $$
Commented by LEKOUMA last updated on 10/Nov/21

$${Thanks} \\ $$
Answered by mr W last updated on 10/Nov/21
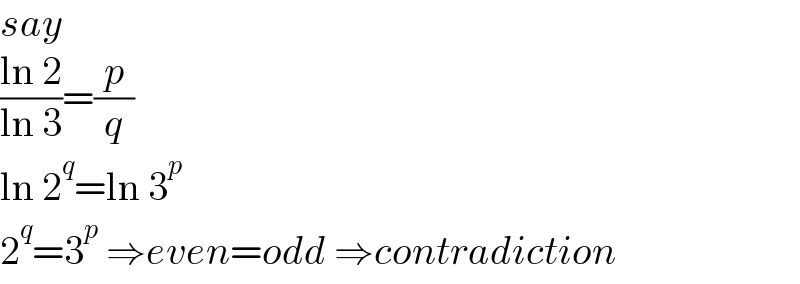
$${say} \\ $$$$\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{3}}=\frac{{p}}{{q}} \\ $$$$\mathrm{ln}\:\mathrm{2}^{{q}} =\mathrm{ln}\:\mathrm{3}^{{p}} \\ $$$$\mathrm{2}^{{q}} =\mathrm{3}^{{p}} \:\Rightarrow{even}={odd}\:\Rightarrow{contradiction} \\ $$
Commented by LEKOUMA last updated on 10/Nov/21

$${Thanks} \\ $$
