Question Number 158984 by LEKOUMA last updated on 11/Nov/21
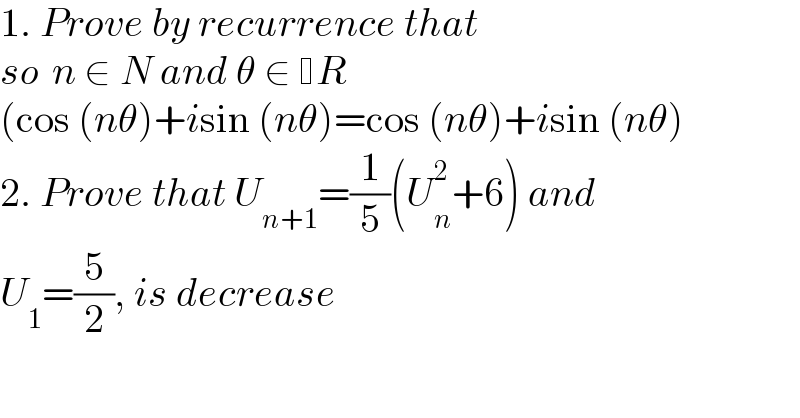
$$\mathrm{1}.\:{Prove}\:{by}\:{recurrence}\:{that}\: \\ $$$${so}\:\:{n}\:\in\:{N}\:{and}\:\theta\:\in\: {R}\: \\ $$$$\left(\mathrm{cos}\:\left({n}\theta\right)+{i}\mathrm{sin}\:\left({n}\theta\right)=\mathrm{cos}\:\left({n}\theta\right)+{i}\mathrm{sin}\:\left({n}\theta\right)\right. \\ $$$$\mathrm{2}.\:{Prove}\:{that}\:{U}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{5}}\left({U}_{{n}} ^{\mathrm{2}} +\mathrm{6}\right)\:{and} \\ $$$${U}_{\mathrm{1}} =\frac{\mathrm{5}}{\mathrm{2}},\:{is}\:{decrease} \\ $$$$ \\ $$
