Menu Close

1-prove-that-arctan-a-arctanb-arctan-a-b-1-ab-with-ab-1-2-find-the-value-of-S-N-n-1-N-1-n-arctan-2n-1-n-2-n-1-

Tinku Tara 0 Comments
Pin




Question Number 57848 by Abdo msup. last updated on 13/Apr/19
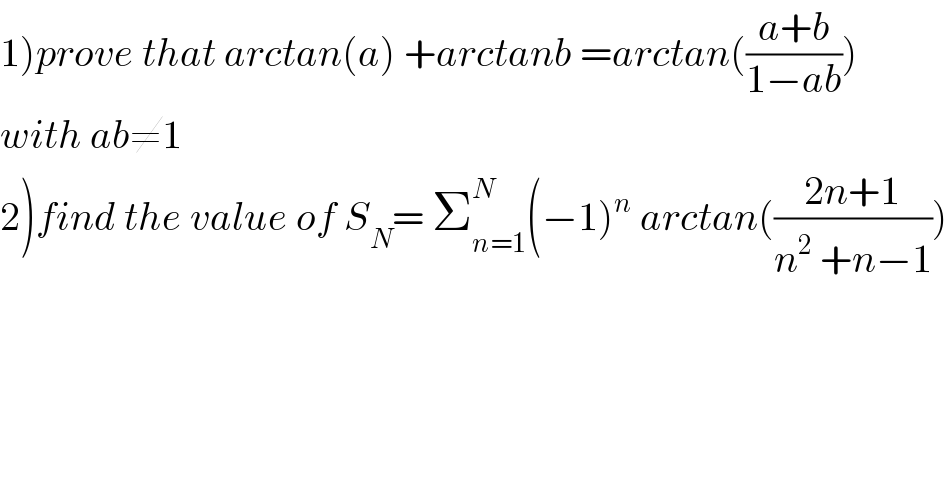
1)prove that arctan(a) +arctanb =arctan(((a+b)/(1−ab))) with ab≠1 2)find the value of S_N = Σ_(n=1) ^N (−1)^n arctan(((2n+1)/(n^2 +n−1)))
$$\left.\mathrm{1}\right){prove}\:{that}\:{arctan}\left({a}\right)\:+{arctanb}\:={arctan}\left(\frac{{a}+{b}}{\mathrm{1}−{ab}}\right)\: \\ $$$${with}\:{ab}\neq\mathrm{1} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:{S}_{{N}} =\:\sum_{{n}=\mathrm{1}} ^{{N}} \left(−\mathrm{1}\right)^{{n}} \:{arctan}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{{n}^{\mathrm{2}} \:+{n}−\mathrm{1}}\right) \\ $$
Commented by maxmathsup by imad last updated on 13/Apr/19
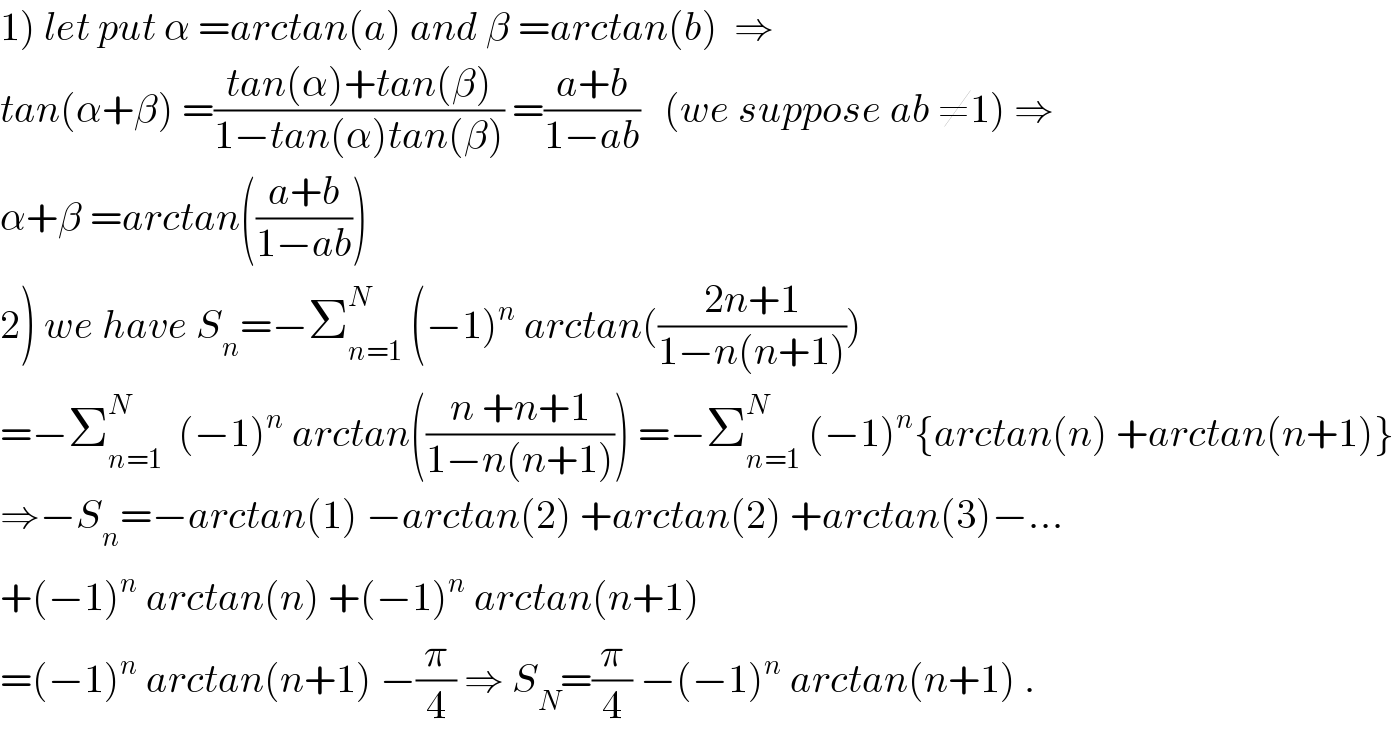
1) let put α =arctan(a) and β =arctan(b) ⇒ tan(α+β) =((tan(α)+tan(β))/(1−tan(α)tan(β))) =((a+b)/(1−ab)) (we suppose ab ≠1) ⇒ α+β =arctan(((a+b)/(1−ab))) 2) we have S_n =−Σ_(n=1) ^N (−1)^n arctan(((2n+1)/(1−n(n+1)))) =−Σ_(n=1) ^N (−1)^n arctan(((n +n+1)/(1−n(n+1)))) =−Σ_(n=1) ^N (−1)^n {arctan(n) +arctan(n+1)} ⇒−S_n =−arctan(1) −arctan(2) +arctan(2) +arctan(3)−... +(−1)^n arctan(n) +(−1)^n arctan(n+1) =(−1)^n arctan(n+1) −(π/4) ⇒ S_N =(π/4) −(−1)^n arctan(n+1) .
$$\left.\mathrm{1}\right)\:{let}\:{put}\:\alpha\:={arctan}\left({a}\right)\:{and}\:\beta\:={arctan}\left({b}\right)\:\:\Rightarrow \\ $$$${tan}\left(\alpha+\beta\right)\:=\frac{{tan}\left(\alpha\right)+{tan}\left(\beta\right)}{\mathrm{1}−{tan}\left(\alpha\right){tan}\left(\beta\right)}\:=\frac{{a}+{b}}{\mathrm{1}−{ab}}\:\:\:\left({we}\:{suppose}\:{ab}\:\neq\mathrm{1}\right)\:\Rightarrow \\ $$$$\alpha+\beta\:={arctan}\left(\frac{{a}+{b}}{\mathrm{1}−{ab}}\right) \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{S}_{{n}} =−\sum_{{n}=\mathrm{1}} ^{{N}} \:\left(−\mathrm{1}\right)^{{n}} \:{arctan}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{1}−{n}\left({n}+\mathrm{1}\right)}\right) \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{{N}} \:\:\left(−\mathrm{1}\right)^{{n}} \:{arctan}\left(\frac{{n}\:+{n}+\mathrm{1}}{\mathrm{1}−{n}\left({n}+\mathrm{1}\right)}\right)\:=−\sum_{{n}=\mathrm{1}} ^{{N}} \:\left(−\mathrm{1}\right)^{{n}} \left\{{arctan}\left({n}\right)\:+{arctan}\left({n}+\mathrm{1}\right)\right\} \\ $$$$\Rightarrow−{S}_{{n}} =−{arctan}\left(\mathrm{1}\right)\:−{arctan}\left(\mathrm{2}\right)\:+{arctan}\left(\mathrm{2}\right)\:+{arctan}\left(\mathrm{3}\right)−… \\ $$$$+\left(−\mathrm{1}\right)^{{n}} \:{arctan}\left({n}\right)\:+\left(−\mathrm{1}\right)^{{n}} \:{arctan}\left({n}+\mathrm{1}\right) \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \:{arctan}\left({n}+\mathrm{1}\right)\:−\frac{\pi}{\mathrm{4}}\:\Rightarrow\:{S}_{{N}} =\frac{\pi}{\mathrm{4}}\:−\left(−\mathrm{1}\right)^{{n}} \:{arctan}\left({n}+\mathrm{1}\right)\:. \\ $$
Commented by maxmathsup by imad last updated on 13/Apr/19
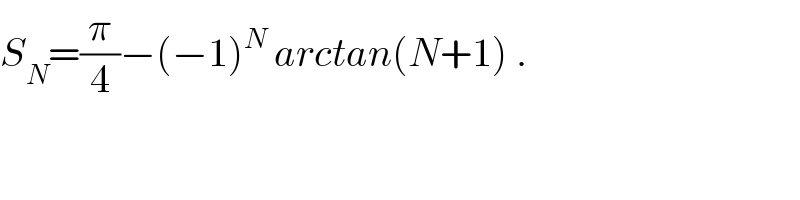
S_N =(π/4)−(−1)^N arctan(N+1) .
$${S}_{{N}} =\frac{\pi}{\mathrm{4}}−\left(−\mathrm{1}\right)^{{N}} \:{arctan}\left({N}+\mathrm{1}\right)\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *