Question Number 34596 by abdo mathsup 649 cc last updated on 08/May/18
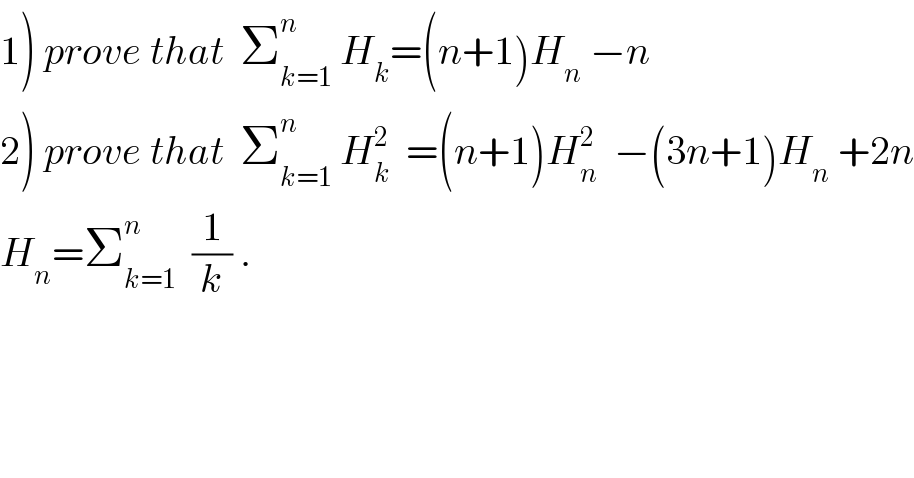
$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{H}_{{k}} =\left({n}+\mathrm{1}\right){H}_{{n}} \:−{n} \\ $$$$\left.\mathrm{2}\right)\:{prove}\:{that}\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{H}_{{k}} ^{\mathrm{2}} \:\:=\left({n}+\mathrm{1}\right){H}_{{n}} ^{\mathrm{2}} \:\:−\left(\mathrm{3}{n}+\mathrm{1}\right){H}_{{n}} \:+\mathrm{2}{n} \\ $$$${H}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}}\:. \\ $$
