Question Number 51984 by maxmathsup by imad last updated on 01/Jan/19
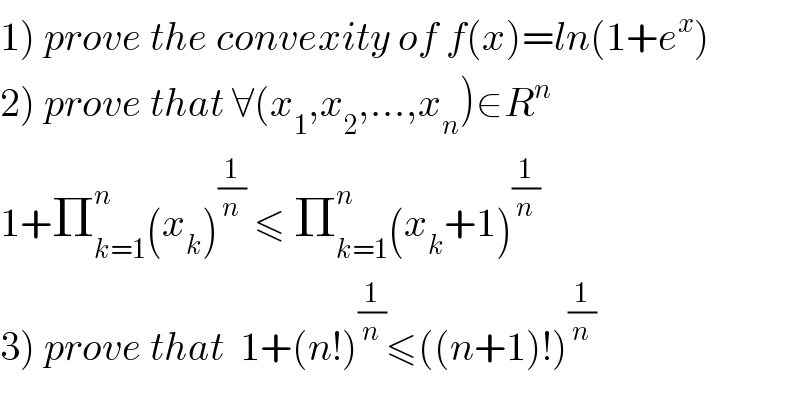
$$\left.\mathrm{1}\right)\:{prove}\:{the}\:{convexity}\:{of}\:{f}\left({x}\right)={ln}\left(\mathrm{1}+{e}^{{x}} \right) \\ $$$$\left.\mathrm{2}\right)\:{prove}\:{that}\:\forall\left({x}_{\mathrm{1}} ,{x}_{\mathrm{2}} ,…,{x}_{{n}} \right)\in{R}^{{n}} \\ $$$$\mathrm{1}+\prod_{{k}=\mathrm{1}} ^{{n}} \left({x}_{{k}} \right)^{\frac{\mathrm{1}}{{n}}} \:\leqslant\:\prod_{{k}=\mathrm{1}} ^{{n}} \left({x}_{{k}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\left.\mathrm{3}\right)\:{prove}\:{that}\:\:\mathrm{1}+\left({n}!\right)^{\frac{\mathrm{1}}{{n}}} \leqslant\left(\left({n}+\mathrm{1}\right)!\right)^{\frac{\mathrm{1}}{{n}}} \\ $$
