Question Number 146736 by mnjuly1970 last updated on 15/Jul/21
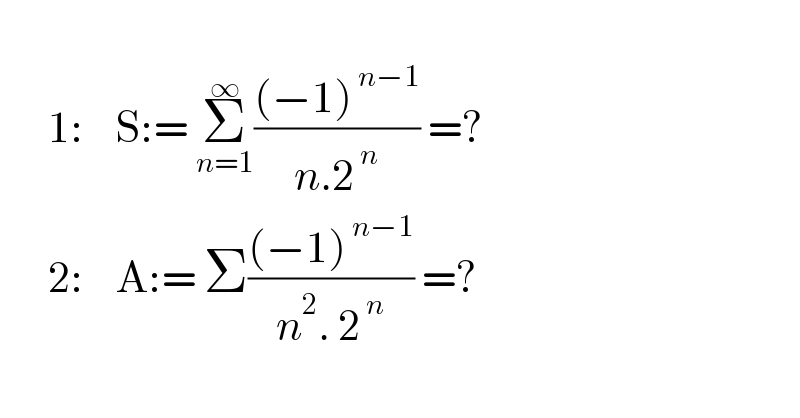
$$ \\ $$$$\:\:\:\:\:\:\mathrm{1}:\:\:\:\:\mathrm{S}:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\:{n}−\mathrm{1}} }{{n}.\mathrm{2}^{\:{n}} }\:=? \\ $$$$\:\:\:\:\:\:\mathrm{2}:\:\:\:\:\mathrm{A}:=\:\Sigma\frac{\left(−\mathrm{1}\right)^{\:{n}−\mathrm{1}} }{{n}^{\mathrm{2}} .\:\mathrm{2}^{\:{n}} }\:=? \\ $$
Answered by Olaf_Thorendsen last updated on 15/Jul/21
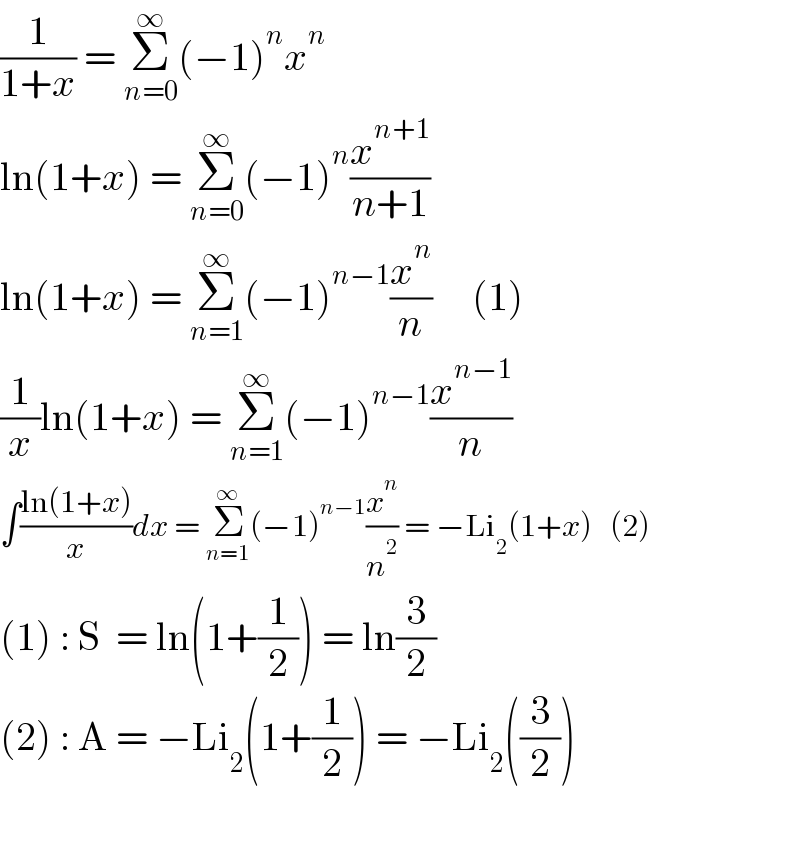
$$\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \\ $$$$\mathrm{ln}\left(\mathrm{1}+{x}\right)\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\: \\ $$$$\mathrm{ln}\left(\mathrm{1}+{x}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{{x}^{{n}} }{{n}}\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{{x}}\mathrm{ln}\left(\mathrm{1}+{x}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{{x}^{{n}−\mathrm{1}} }{{n}} \\ $$$$\int\frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{{x}^{{n}} }{{n}^{\mathrm{2}} }\:=\:−\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}+{x}\right)\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\::\:\mathrm{S}\:\:=\:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{ln}\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\::\:\mathrm{A}\:=\:−\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:−\mathrm{Li}_{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 15/Jul/21
$${thanks}\:{alot}\:{master}…. \\ $$
