Menu Close

1-sec-1-x-2-dx-2-x-2-sin-1-3x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 106148 by mohammad17 last updated on 03/Aug/20
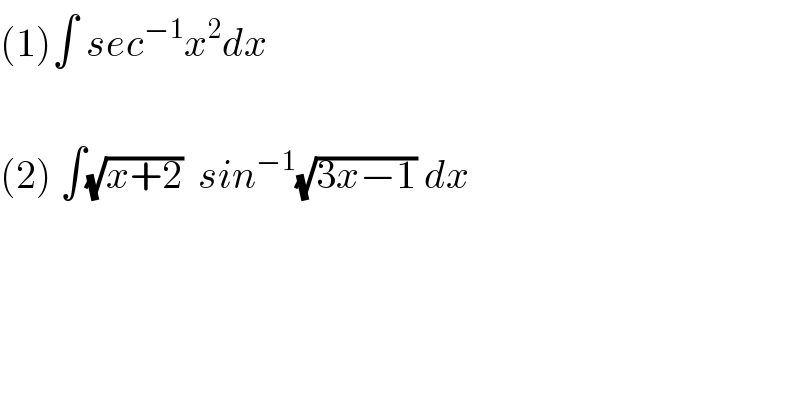
(1)∫ sec^(−1) x^2 dx (2) ∫(√(x+2)) sin^(−1) (√(3x−1)) dx
$$\left(\mathrm{1}\right)\int\:{sec}^{−\mathrm{1}} {x}^{\mathrm{2}} {dx} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\int\sqrt{{x}+\mathrm{2}}\:\:{sin}^{−\mathrm{1}} \sqrt{\mathrm{3}{x}−\mathrm{1}}\:{dx} \\ $$
Answered by bemath last updated on 03/Aug/20
(1) by part → { ((u = sec^(−1) (x^2 ))),((v = x)) :} x^2 =sec u ⇒2x dx = sec u tan u du du = ((2x)/(x^2 (√(x^2 −1)))) dx I = x.sec^(−1) (x^2 )−∫ ((2x^2 )/(x^2 (√(x^2 −1)))) dx I= xsec^(−1) (x^2 )−2∫ (dx/( (√(x^2 −1)))) I_2 =∫(dx/( (√(x^2 −1)))) [ set x = sec ♭ ] I_2 = ∫ ((sec ♭ tan ♭ )/(tan ♭)) d♭= ln ∣sec ♭+tan ♭∣+c I_2 =ln ∣x+(√(x^2 −1))∣ +c then we have I=x.sec^(−1) (x^2 )−2I_2
$$\left(\mathrm{1}\right)\:\mathrm{by}\:\mathrm{part}\:\rightarrow\begin{cases}{\mathrm{u}\:=\:\mathrm{sec}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} \right)}\\{\mathrm{v}\:=\:\mathrm{x}}\end{cases} \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{sec}\:\mathrm{u}\:\Rightarrow\mathrm{2x}\:\mathrm{dx}\:=\:\mathrm{sec}\:\mathrm{u}\:\mathrm{tan}\:\mathrm{u}\:\mathrm{du} \\ $$$$\mathrm{du}\:=\:\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} \:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\:\mathrm{dx} \\ $$$$\mathrm{I}\:=\:\mathrm{x}.\mathrm{sec}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} \right)−\int\:\frac{\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\:\mathrm{dx} \\ $$$$\mathrm{I}=\:\mathrm{xsec}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2}\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\mathrm{I}_{\mathrm{2}} =\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\:\left[\:\mathrm{set}\:\mathrm{x}\:=\:\mathrm{sec}\:\flat\:\right] \\ $$$$\mathrm{I}_{\mathrm{2}} =\:\int\:\frac{\mathrm{sec}\:\flat\:\mathrm{tan}\:\flat\:}{\mathrm{tan}\:\flat}\:\mathrm{d}\flat=\:\mathrm{ln}\:\mid\mathrm{sec}\:\flat+\mathrm{tan}\:\flat\mid+\mathrm{c} \\ $$$$\mathrm{I}_{\mathrm{2}} =\mathrm{ln}\:\mid\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\mid\:+\mathrm{c} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{have}\:\mathrm{I}=\mathrm{x}.\mathrm{sec}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2I}_{\mathrm{2}} \\ $$
Commented by Her_Majesty last updated on 03/Aug/20
there′s an error it′s ∫(2/( (√(x^4 −1))))dx
$${there}'{s}\:{an}\:{error} \\ $$$${it}'{s}\:\int\frac{\mathrm{2}}{\:\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}}{dx} \\ $$
Answered by mathmax by abdo last updated on 03/Aug/20
2) I =∫(√(x+2))arcsin((√(3x−1)))dx changement (√(3x−1))=t give 3x−1 =t^2 ⇒x =(1/3)(t^2 +1) ⇒I =∫ (√((1/3)t^2 +(7/3)))arcsin(t)((2/3)t)dt =(2/(3(√3))) ∫ t(√(t^2 +7)) arsin(t)dt by parts ∫ t(√(t^2 +7))arcsint dt =(1/3)(t^2 +7)^(3/2) −(1/3)∫(t^2 +7)^(3/2) (dt/( (√(1−t^2 )))) and ∫ (t^(2 ) +7)^(3/2) (dt/( (√(1−t^2 )))) =_(t =sinu) ∫ (sin^2 u+7)^(3/2) ((cosu)/(cosu)) du =∫ (sin^2 u +7)^(3/2) du =∫(8−cos^2 u)^(3/2) du ...be continued....
$$\left.\mathrm{2}\right)\:\mathrm{I}\:=\int\sqrt{\mathrm{x}+\mathrm{2}}\mathrm{arcsin}\left(\sqrt{\mathrm{3x}−\mathrm{1}}\right)\mathrm{dx}\:\:\mathrm{changement}\:\sqrt{\mathrm{3x}−\mathrm{1}}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{3x}−\mathrm{1}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\:\Rightarrow\mathrm{I}\:=\int\:\sqrt{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{7}}{\mathrm{3}}}\mathrm{arcsin}\left(\mathrm{t}\right)\left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{t}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\:\int\:\:\mathrm{t}\sqrt{\mathrm{t}^{\mathrm{2}} \:+\mathrm{7}}\:\mathrm{arsin}\left(\mathrm{t}\right)\mathrm{dt}\:\:\mathrm{by}\:\mathrm{parts}\:\int\:\mathrm{t}\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{7}}\mathrm{arcsint}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{7}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}\int\left(\mathrm{t}^{\mathrm{2}} +\mathrm{7}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\:\:\mathrm{and} \\ $$$$\int\:\left(\mathrm{t}^{\mathrm{2}\:} +\mathrm{7}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\:=_{\mathrm{t}\:=\mathrm{sinu}} \:\:\:\int\:\:\left(\mathrm{sin}^{\mathrm{2}} \mathrm{u}+\mathrm{7}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\frac{\mathrm{cosu}}{\mathrm{cosu}}\:\mathrm{du} \\ $$$$=\int\:\left(\mathrm{sin}^{\mathrm{2}} \mathrm{u}\:+\mathrm{7}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{du}\:=\int\left(\mathrm{8}−\mathrm{cos}^{\mathrm{2}} \mathrm{u}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{du}\:\:…\mathrm{be}\:\mathrm{continued}…. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *