Menu Close

1-Show-that-0-pi-xdx-a-2-sin-2-x-b-2-cos-2-x-2-pi-2-a-2-b-2-4a-3-b-3-2-The-density-at-the-point-x-y-of-a-lamina-bounded-by-the-circle-x-2-y-2-2ax-0-i

Tinku Tara 0 Comments
Pin




Question Number 94992 by Mr.D.N. last updated on 22/May/20
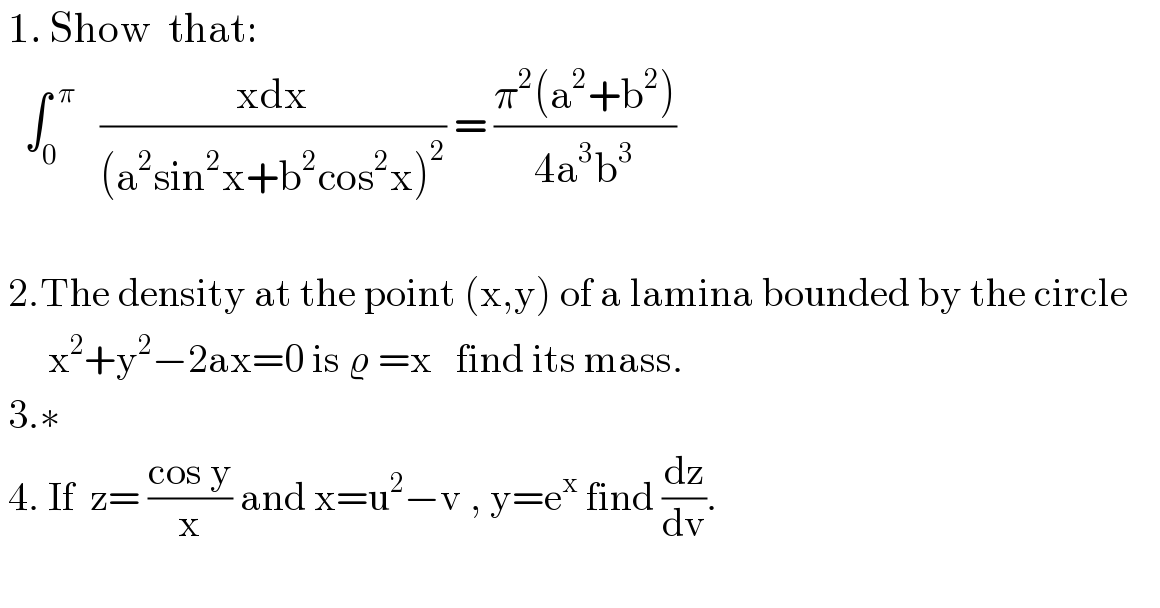
1. Show that: ∫_0 ^( π) ((xdx)/((a^2 sin^2 x+b^2 cos^2 x)^2 )) = ((π^2 (a^2 +b^2 ))/(4a^3 b^3 )) 2.The density at the point (x,y) of a lamina bounded by the circle x^2 +y^2 −2ax=0 is ϱ =x find its mass. 3.∗ 4. If z= ((cos y)/x) and x=u^2 −v , y=e^x find (dz/dv).
$$\:\mathrm{1}.\:\mathrm{Show}\:\:\mathrm{that}: \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\:\pi} \:\:\:\frac{\mathrm{xdx}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\:=\:\frac{\pi^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{4a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} } \\ $$$$\:\: \\ $$$$\:\mathrm{2}.\mathrm{The}\:\mathrm{density}\:\mathrm{at}\:\mathrm{the}\:\mathrm{point}\:\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{of}\:\mathrm{a}\:\mathrm{lamina}\:\mathrm{bounded}\:\mathrm{by}\:\mathrm{the}\:\mathrm{circle} \\ $$$$\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2ax}=\mathrm{0}\:\mathrm{is}\:\varrho\:=\mathrm{x}\:\:\:\mathrm{find}\:\mathrm{its}\:\mathrm{mass}. \\ $$$$\:\mathrm{3}.\ast \\ $$$$\:\mathrm{4}.\:\mathrm{If}\:\:\mathrm{z}=\:\frac{\mathrm{cos}\:\mathrm{y}}{\mathrm{x}}\:\mathrm{and}\:\mathrm{x}=\mathrm{u}^{\mathrm{2}} −\mathrm{v}\:,\:\mathrm{y}=\mathrm{e}^{\mathrm{x}} \:\mathrm{find}\:\frac{\mathrm{dz}}{\mathrm{dv}}. \\ $$$$\:\: \\ $$
Answered by bobhans last updated on 22/May/20
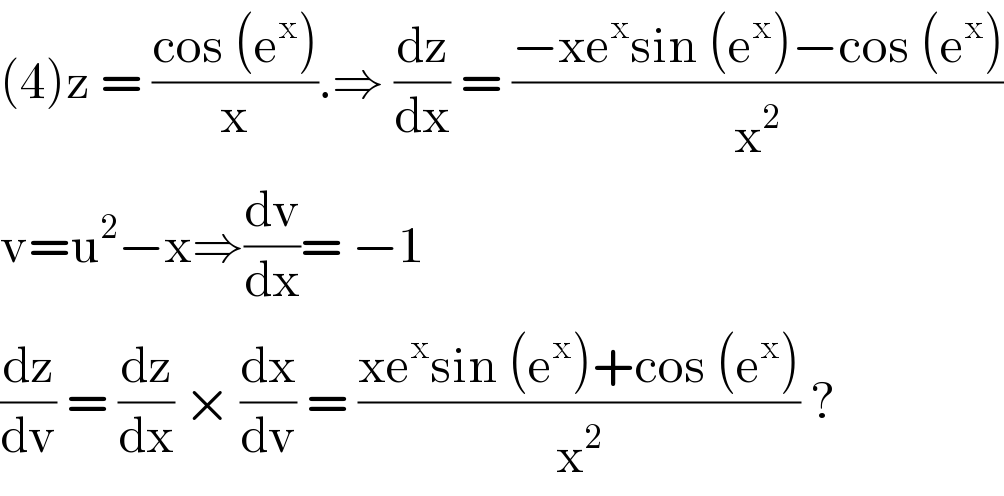
(4)z = ((cos (e^x ))/x).⇒ (dz/dx) = ((−xe^x sin (e^x )−cos (e^x ))/x^2 ) v=u^2 −x⇒(dv/dx)= −1 (dz/dv) = (dz/dx) × (dx/dv) = ((xe^x sin (e^x )+cos (e^x ))/x^2 ) ?
$$\left(\mathrm{4}\right)\mathrm{z}\:=\:\frac{\mathrm{cos}\:\left(\mathrm{e}^{\mathrm{x}} \right)}{\mathrm{x}}.\Rightarrow\:\frac{\mathrm{dz}}{\mathrm{dx}}\:=\:\frac{−\mathrm{xe}^{\mathrm{x}} \mathrm{sin}\:\left(\mathrm{e}^{\mathrm{x}} \right)−\mathrm{cos}\:\left(\mathrm{e}^{\mathrm{x}} \right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{v}=\mathrm{u}^{\mathrm{2}} −\mathrm{x}\Rightarrow\frac{\mathrm{dv}}{\mathrm{dx}}=\:−\mathrm{1} \\ $$$$\frac{\mathrm{dz}}{\mathrm{dv}}\:=\:\frac{\mathrm{dz}}{\mathrm{dx}}\:×\:\frac{\mathrm{dx}}{\mathrm{dv}}\:=\:\frac{\mathrm{xe}^{\mathrm{x}} \mathrm{sin}\:\left(\mathrm{e}^{\mathrm{x}} \right)+\mathrm{cos}\:\left(\mathrm{e}^{\mathrm{x}} \right)}{\mathrm{x}^{\mathrm{2}} }\:?\: \\ $$
Commented by Mr.D.N. last updated on 22/May/20
thank you nice solution��
Answered by Ar Brandon last updated on 22/May/20
1\I=∫_0 ^π ((xdx)/((a^2 sin^2 x+b^2 cos^2 x)^2 )) x=π−u⇒dx=−du⇒I=∫_0 ^π (π/((a^2 sin^2 u+b^2 cos^2 u)^2 ))du−I ⇒2I=∫_0 ^π (π/((a^2 sin^2 x+b^2 cos^2 x)^2 ))dx=π∫_0 ^π ((sec^4 x)/((a^2 tan^2 x+b^2 )^2 ))dx ⇒2I=_(t=tanx) π∫_(+0) ^(−0) ((t^2 +1)/((a^2 t^2 +b^2 )^2 ))dt=π∫_(+0) ^(−0) [((1/a^2 )/(a^2 t^2 +b^2 ))+(((a^2 −b^2 )/a^2 )/((a^2 t^2 +b^2 )^2 ))]dt 2I=(π/(a^2 b^2 ))∫_(+0) ^(−0) (1/(((a/b)t)^2 +1))dt+((π(a^2 −b^2 ))/(a^2 b^4 ))∫_(+0) ^(−0) (1/([((a/b)t)^2 +1]^2 ))dt 2I=(π/(a^3 b))[tan^(−1) ((a/b)t)]_(+0) ^(−0) +((π(a^2 −b^2 ))/(a^2 b^4 ))∫_0 ^π (((b/a)sec^2 θ)/(sec^4 θ))dθ =(π^2 /(a^3 b))+((π(a^2 −b^2 ))/(2a^3 b^3 ))∫_0 ^π (1+cos 2θ)dθ=(π^2 /(a^3 b))+((π(a^2 −b^2 ))/(2a^3 b^3 ))[θ+((sin2θ)/2)]_0 ^π =(π^2 /(a^3 b))+((π^2 (a^2 −b^2 ))/(2a^3 b^3 ))=((2π^2 b^2 +a^2 π^2 −π^2 b^2 )/(2a^3 b^3 ))=((π^2 (a^2 +b^2 ))/(2a^3 b^3 )) ⇒∫_0 ^π ((xdx)/((a^2 sin^2 x+b^2 cos^2 x)^2 ))=((π^2 (a^2 +b^2 ))/(4a^3 b^3 ))
$$\mathrm{1}\backslash\mathrm{I}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{xdx}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}=\pi−\mathrm{u}\Rightarrow\mathrm{dx}=−\mathrm{du}\Rightarrow\mathrm{I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{u}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{u}\right)^{\mathrm{2}} }\mathrm{du}−\mathrm{I} \\ $$$$\Rightarrow\mathrm{2I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}=\pi\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{4}} \mathrm{x}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{2I}\underset{\mathrm{t}=\mathrm{tanx}} {=}\pi\int_{+\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}=\pi\int_{+\mathrm{0}} ^{−\mathrm{0}} \left[\frac{\mathrm{1}/\mathrm{a}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }+\frac{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)/\mathrm{a}^{\mathrm{2}} }{\left(\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\right]\mathrm{dt} \\ $$$$\mathrm{2I}=\frac{\pi}{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }\int_{+\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{1}}{\left(\frac{\mathrm{a}}{\mathrm{b}}\mathrm{t}\right)^{\mathrm{2}} +\mathrm{1}}\mathrm{dt}+\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{4}} }\int_{+\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{1}}{\left[\left(\frac{\mathrm{a}}{\mathrm{b}}\mathrm{t}\right)^{\mathrm{2}} +\mathrm{1}\right]^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{2I}=\frac{\pi}{\mathrm{a}^{\mathrm{3}} \mathrm{b}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{b}}\mathrm{t}\right)\right]_{+\mathrm{0}} ^{−\mathrm{0}} +\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{4}} }\int_{\mathrm{0}} ^{\pi} \frac{\left(\mathrm{b}/\mathrm{a}\right)\mathrm{sec}^{\mathrm{2}} \theta}{\mathrm{sec}^{\mathrm{4}} \theta}\mathrm{d}\theta \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{a}^{\mathrm{3}} \mathrm{b}}+\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{2a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)\mathrm{d}\theta=\frac{\pi^{\mathrm{2}} }{\mathrm{a}^{\mathrm{3}} \mathrm{b}}+\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{2a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }\left[\theta+\frac{\mathrm{sin2}\theta}{\mathrm{2}}\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{a}^{\mathrm{3}} \mathrm{b}}+\frac{\pi^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{2a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }=\frac{\mathrm{2}\pi^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \pi^{\mathrm{2}} −\pi^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }{\mathrm{2a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }=\frac{\pi^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{2a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{xdx}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{4a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }\:\:\: \\ $$
Commented by Mr.D.N. last updated on 22/May/20
lim is all[right you might be mistek some way]
$$\:{lim}\:{is}\:{all}\left[{right}\:{you}\:{might}\:{be}\:{mistek}\:\:{some}\:{way}\right] \\ $$
Commented by Ar Brandon last updated on 22/May/20
Okay let's check my solution and see if I might have made some mistakes.
Commented by niroj last updated on 22/May/20
let me solve then you find your correction just taken few time then you find easily where is a error....��
Commented by Ar Brandon last updated on 22/May/20
Okay, I'm grateful. Thanks
Commented by Ar Brandon last updated on 22/May/20
Hey hold on. I wanna give it a last try.����
Commented by Ar Brandon last updated on 22/May/20
Thanks for your patience Mr. Niroj ��
Commented by Ar Brandon last updated on 22/May/20
I found my mistake.�� It was necessary for me to respect the signs. That is, distinguish between –0 and +0��
Answered by niroj last updated on 22/May/20
1. I= ∫_0 ^( π) (( xdx)/((a^2 sin^2 x+b^2 cos^2 x)^2 )) .....(i) = ∫_0 ^( π) (((π−x)dx)/({a^2 sin^2 (π−a)+b^2 cos^2 (π−a)}^2 )) I = ∫_0 ^( π) (((π−x)dx)/((a^2 sin^2 x+b^2 cos^2 x)^2 ))....(ii) Added (i)+(ii) 2I= ∫_0 ^π (π/((a^2 sin^2 x+b^2 cos^2 x)^2 ))dx I= (π/2)×2∫_0 ^( (π/2)) (( 1)/((a^2 sin^2 x+b^2 cos^2 x)^2 ))dx = π ∫_0 ^( (π/2)) (( 1)/((a^2 sin^2 x+b^2 cos^2 x)^2 ))dx Divide numerator& denominator by (1/(cos^4 x)) = π∫_0 ^( (π/2)) (( sec^4 xdx)/({(1/(cos^2 x))(a^2 sin^2 x+b^2 cos^2 x)}^2 )) = π ∫_0 ^( (π/2)) (((tan^2 x+1) sec^2 x dx)/((a^2 tan^2 x+b^2 )^2 )) Put tan x = t sec^2 xdx=dt If x=(π/2) ⇒ t=∞ If x=0 ⇒ t=0 Now, π∫_0 ^( ∞) (((t^2 +1)dt)/((a^2 t^2 +b^2 )^2 )) = (π/a^2 )∫_0 ^( ∞) ((a^2 t^2 +a^2 )/((a^2 t^2 +b^2 )^2 ))dt = (π/a^2 ) ∫_(0 ) ^( ∞) (( (a^2 −b^2 )+(a^2 t^2 +b^2 ))/((a^2 t^2 +b^2 )^2 ))dt = (π/a^2 )∫_0 ^( ∞) (((a^2 −b^2 ))/((a^2 t^2 +b^2 )^2 ))dt+ (π/a^2 )∫_0 ^∞ (1/(a^2 t^2 +b^2 ))dt = ((π(a^2 −b^2 ))/a^2 )∫_0 ^( ∞) (1/((a^2 t^2 +b^2 )^2 ))dt+(π/(a^2 .a^2 ))∫_0 ^∞ (1/((t)^2 +((b/a))^2 ))dt here, I= I_1 +I_2 I_1 = ((π(a^2 −b^2 ))/a^2 )∫_0 ^( ∞) (1/((a^2 t^2 +b^2 )^2 ))dt Put, at= b tanθ adt= b sec^2 θdθ dt= (b/a) sec^2 θdθ If t=∞ ⇒ θ= (π/2) If t=0 ⇒ θ=0 ((π(a^2 −b^2 ))/a^2 )(b/a)∫_0 ^( (π/2)) ((sec^2 θdθ)/((b^2 tan^2 θ+b^2 )^2 )) = ((π(a^2 −b^2 )b)/a^3 )∫_0 ^(π/2) ((sec^2 θdθ)/(b^4 .sec^4 θ)) = ((π(a^2 −b^2 ))/(a^3 b^3 ))∫_0 ^(π/2) cos^2 θdθ cos2θ= 1−2cos^2 θ⇒ cos^2 θ =((1−cos2θ)/2) [ (1/2)∫(1−cos2θ)dθ]_0 ^(π/2) = [ (1/2)(θ − ((sin2θ)/2))]_0 ^(π/2) ⇒ [(1/2)((π/2)−((sin2×(π/2))/2))−0] = (π/4) I_1 = ((π(a^2 −b^2 ))/(a^3 b^3 ))×(π/4) Again for I_2 = (π/a^4 )[ (1/(b/a)) tan^(−1) (t/(b/a))]_0 ^∞ = (π/a^4 )[ (a/b)tan^(−1) ((at)/b)]_0 ^∞ = (π/a^4 )[ (a/b)×(π/2)−0] = (π^2 /(2a^3 b)) Now complete solution I= I_1 +I_2 = ((π^2 (a^2 −b^2 ))/(4a^3 b^3 ))+ (π^2 /(2a^3 b)) = (π^2 /(2a^3 b))(((a^2 −b^2 )/(2b^2 ))+1) = (π^2 /(2a^3 b))(((a^2 −b^2 +2b^2 )/(2b^2 ))) = ((π^2 (a^2 +b^2 ))/(4a^3 b^3 )) //. Which is required to proof.
$$\mathrm{1}.\:\:\mathrm{I}=\:\int_{\mathrm{0}} ^{\:\:\pi} \:\frac{\:\mathrm{xdx}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\:…..\left(\mathrm{i}\right) \\ $$$$\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\pi} \:\frac{\left(\pi−\mathrm{x}\right)\mathrm{dx}}{\left\{\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\pi−\mathrm{a}\right)+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\left(\pi−\mathrm{a}\right)\right\}^{\mathrm{2}} } \\ $$$$\:\: \\ $$$$\:\:\:\:\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\pi} \:\frac{\left(\pi−\mathrm{x}\right)\mathrm{dx}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }….\left(\mathrm{ii}\right) \\ $$$$\:\mathrm{Added}\:\left(\mathrm{i}\right)+\left(\mathrm{ii}\right) \\ $$$$\:\:\mathrm{2I}=\:\int_{\mathrm{0}} ^{\pi} \:\frac{\pi}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:\:\:\mathrm{I}=\:\frac{\pi}{\mathrm{2}}×\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\:\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:\:=\:\pi\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\:\:\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\mathrm{Divide}\:\mathrm{numerator\&}\:\mathrm{denominator}\:\mathrm{by}\:\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{4}} \mathrm{x}} \\ $$$$\:\:\:\:=\:\pi\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\:\mathrm{sec}^{\mathrm{4}} \mathrm{xdx}}{\left\{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\right\}^{\mathrm{2}} } \\ $$$$\:\:=\:\pi\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\:\frac{\left(\mathrm{tan}^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)\:\mathrm{sec}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\mathrm{Put}\:\:\mathrm{tan}\:\mathrm{x}\:=\:\mathrm{t} \\ $$$$\:\:\:\:\:\:\:\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}=\mathrm{dt} \\ $$$$\:\:\mathrm{If}\:\mathrm{x}=\frac{\pi}{\mathrm{2}}\:\Rightarrow\:\mathrm{t}=\infty \\ $$$$\:\mathrm{If}\:\mathrm{x}=\mathrm{0}\:\Rightarrow\:\:\mathrm{t}=\mathrm{0} \\ $$$$\:\:\:\mathrm{N}{o}\mathrm{w}, \\ $$$$\:\:\:\pi\int_{\mathrm{0}} ^{\:\infty} \:\:\frac{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{dt}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:=\:\frac{\pi}{\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }{\left(\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:=\:\:\frac{\pi}{\mathrm{a}^{\mathrm{2}} }\:\int_{\mathrm{0}\:} ^{\:\infty} \:\:\:\frac{\:\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)+\left(\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:=\:\frac{\pi}{\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\:\infty} \:\frac{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}+\:\frac{\pi}{\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:=\:\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}+\frac{\pi}{\mathrm{a}^{\mathrm{2}} .\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{t}\right)^{\mathrm{2}} +\left(\frac{\mathrm{b}}{\mathrm{a}}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:\mathrm{here},\:\mathrm{I}=\:\mathrm{I}_{\mathrm{1}} +\mathrm{I}_{\mathrm{2}} \\ $$$$\:\:\mathrm{I}_{\mathrm{1}} =\:\:\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:\:\:\:\mathrm{Put},\:\mathrm{at}=\:\mathrm{b}\:\mathrm{tan}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{adt}=\:\mathrm{b}\:\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:\:\mathrm{dt}=\:\frac{\mathrm{b}}{\mathrm{a}}\:\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\:\:\mathrm{If}\:\:\mathrm{t}=\infty\:\Rightarrow\:\theta=\:\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\mathrm{If}\:\mathrm{t}=\mathrm{0}\:\Rightarrow\:\theta=\mathrm{0} \\ $$$$\:\:\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} }\frac{\mathrm{b}}{\mathrm{a}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta}{\left(\mathrm{b}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \theta+\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:=\:\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)\mathrm{b}}{\mathrm{a}^{\mathrm{3}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta}{\mathrm{b}^{\mathrm{4}} .\mathrm{sec}^{\mathrm{4}} \theta} \\ $$$$\:=\:\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\:\:\:\mathrm{cos2}\theta=\:\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \theta\Rightarrow\:\mathrm{cos}^{\mathrm{2}} \theta\:=\frac{\mathrm{1}−\mathrm{cos2}\theta}{\mathrm{2}} \\ $$$$\:\:\:\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}−\mathrm{cos2}\theta\right)\mathrm{d}\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:=\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}\left(\theta\:−\:\frac{\mathrm{sin2}\theta}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \Rightarrow\:\left[\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{sin2}×\frac{\pi}{\mathrm{2}}}{\mathrm{2}}\right)−\mathrm{0}\right] \\ $$$$\:\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$\:\mathrm{I}_{\mathrm{1}} =\:\:\frac{\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }×\frac{\pi}{\mathrm{4}} \\ $$$$\:\mathrm{Again}\:\:\mathrm{for}\: \\ $$$$\:\:\mathrm{I}_{\mathrm{2}} =\:\frac{\pi}{\mathrm{a}^{\mathrm{4}} }\left[\:\frac{\mathrm{1}}{\frac{\mathrm{b}}{\mathrm{a}}}\:\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{t}}{\frac{\mathrm{b}}{\mathrm{a}}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\:\:\:=\:\frac{\pi}{\mathrm{a}^{\mathrm{4}} }\left[\:\frac{\mathrm{a}}{\mathrm{b}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{at}}{\mathrm{b}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\:\:\:=\:\frac{\pi}{\mathrm{a}^{\mathrm{4}} }\left[\:\frac{\mathrm{a}}{\mathrm{b}}×\frac{\pi}{\mathrm{2}}−\mathrm{0}\right] \\ $$$$\:\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{2a}^{\mathrm{3}} \mathrm{b}} \\ $$$$\:\mathrm{N}{o}\mathrm{w}\:\mathrm{complete}\:\mathrm{solution} \\ $$$$\:\:\mathrm{I}=\:\mathrm{I}_{\mathrm{1}} +\mathrm{I}_{\mathrm{2}} \\ $$$$\:\:=\:\:\frac{\pi^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{4a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }+\:\frac{\pi^{\mathrm{2}} }{\mathrm{2a}^{\mathrm{3}} \mathrm{b}} \\ $$$$\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{2a}^{\mathrm{3}} \mathrm{b}}\left(\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{2b}^{\mathrm{2}} }+\mathrm{1}\right) \\ $$$$\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{2a}^{\mathrm{3}} \mathrm{b}}\left(\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} +\mathrm{2b}^{\mathrm{2}} }{\mathrm{2b}^{\mathrm{2}} }\right) \\ $$$$\:=\:\frac{\pi^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{4a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }\:\://.\: \\ $$$$\:\mathrm{Which}\:\mathrm{is}\:\mathrm{required}\:\mathrm{to}\:\mathrm{proof}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Mr.D.N. last updated on 22/May/20
Thanks for all of you to presents your ability it's really I appreciate.. ������
Answered by niroj last updated on 22/May/20
2. Sol^n : If m be a mass of the lamania,then m= ∫_(R ) ∫ϱ dx dy = ∫_R ∫ϱx dx dy where R being the circle x^2 +y^2 −2ax =0 We know polar transformation x= r cosθ , y= r sinθ then equation of the circle be comes x^2 +y^2 = 2ax i.e. r^2 =2ar cosθ i.e. r=2a cosθ Also, dxdy = r dr dθ The bounded of R of the circle can be described by−(π/2)≤ θ≤(π/2) and 0≤r ≤2a cosθ ∴ m = ∫_(θ=((−π)/2)) ^(π/2) ∫_0 ^( 2a cosθ) r cosθ r dr dθ = ∫_(−π/2) ^(π/2) cosθ ((r^2 /3))_0 ^(2a cosθ) dθ = ∫_(−π/2) ^( π/2) ((8a^3 )/3).cos^4 θ dθ = ((16 a^3 )/3) ∫_0 ^( π/2) cos^4 θdθ by using gamm function = ((16a^3 )/3)(( ⌈4 +(1/2).⌈(1/2))/(2⌈3)) = ((16a^3 )/3). (((3/2).(1/2)(√π) . (√π))/(2.2.1)) = ((16 a^3 )/3).(3/4).(1/4).π = π a^3 ∴ It′s mass = π a^3 //.
$$\:\mathrm{2}.\:\mathrm{Sol}^{\mathrm{n}} : \\ $$$$\:\:\:\mathrm{If}\:\mathrm{m}\:\mathrm{be}\:\mathrm{a}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lamania},\mathrm{then} \\ $$$$\:\mathrm{m}=\:\int_{\mathrm{R}\:} \int\varrho\:\mathrm{dx}\:\mathrm{dy}\:=\:\int_{\mathrm{R}} \int\varrho\mathrm{x}\:\mathrm{dx}\:\mathrm{dy} \\ $$$$\:\:\mathrm{where}\:\mathrm{R}\:\mathrm{being}\:\mathrm{the}\:\mathrm{circle}\: \\ $$$$\:\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2ax}\:=\mathrm{0} \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{polar}\:\mathrm{transformation} \\ $$$$\:\:\mathrm{x}=\:\mathrm{r}\:\mathrm{cos}\theta\:,\:\:\mathrm{y}=\:\mathrm{r}\:\mathrm{sin}\theta \\ $$$$\:\:\mathrm{then}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{be}\:\mathrm{comes} \\ $$$$\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\:\mathrm{2ax}\:\:\mathrm{i}.\mathrm{e}.\:\mathrm{r}^{\mathrm{2}} =\mathrm{2ar}\:\mathrm{cos}\theta\:{i}.{e}.\:\:{r}=\mathrm{2}{a}\:{cos}\theta \\ $$$$\:\:{A}\mathrm{lso},\:\mathrm{dxdy}\:=\:\mathrm{r}\:\mathrm{dr}\:\mathrm{d}\theta \\ $$$$\:\:\:\mathrm{The}\:\mathrm{bounded}\:\mathrm{of}\:\mathrm{R}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{can}\:\mathrm{be}\:\mathrm{described}\:\mathrm{by}−\frac{\pi}{\mathrm{2}}\leqslant\:\theta\leqslant\frac{\pi}{\mathrm{2}}\:\mathrm{and}\: \\ $$$$\:\:\mathrm{0}\leqslant{r}\:\leqslant\mathrm{2a}\:\mathrm{cos}\theta \\ $$$$\:\:\therefore\:\:\mathrm{m}\:=\:\int_{\theta=\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\int_{\mathrm{0}} ^{\:\mathrm{2a}\:\mathrm{cos}\theta} \mathrm{r}\:\mathrm{cos}\theta\:\mathrm{r}\:\mathrm{dr}\:\mathrm{d}\theta \\ $$$$\:\:\:\:=\:\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \:\mathrm{cos}\theta\:\left(\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{3}}\right)_{\mathrm{0}} ^{\mathrm{2a}\:\mathrm{cos}\theta} \mathrm{d}\theta \\ $$$$\:\:\:=\:\int_{−\pi/\mathrm{2}} ^{\:\pi/\mathrm{2}} \:\frac{\mathrm{8a}^{\mathrm{3}} }{\mathrm{3}}.\mathrm{cos}^{\mathrm{4}} \theta\:\mathrm{d}\theta \\ $$$$\:\:=\:\frac{\mathrm{16}\:\mathrm{a}^{\mathrm{3}} }{\mathrm{3}}\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\mathrm{cos}^{\mathrm{4}} \theta\mathrm{d}\theta\: \\ $$$$\:\:\mathrm{by}\:\mathrm{using}\:\mathrm{gamm}\:\mathrm{function} \\ $$$$\:\:=\:\frac{\mathrm{16a}^{\mathrm{3}} }{\mathrm{3}}\frac{\:\:\lceil\mathrm{4}\:+\frac{\mathrm{1}}{\mathrm{2}}.\lceil\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{2}\lceil\mathrm{3}} \\ $$$$\:=\:\frac{\mathrm{16a}^{\mathrm{3}} }{\mathrm{3}}.\:\frac{\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pi}\:.\:\sqrt{\pi}}{\mathrm{2}.\mathrm{2}.\mathrm{1}} \\ $$$$\:=\:\frac{\mathrm{16}\:\mathrm{a}^{\mathrm{3}} }{\mathrm{3}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{4}}.\pi \\ $$$$\:=\:\pi\:\mathrm{a}^{\mathrm{3}} \\ $$$$\:\therefore\:\mathrm{It}'\mathrm{s}\:\mathrm{mass}\:=\:\pi\:\mathrm{a}^{\mathrm{3}} \://. \\ $$$$ \\ $$
Commented by Mr.D.N. last updated on 22/May/20
what nice outstanding��������

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *