Menu Close

1-simplify-A-n-1-2-i-3-n-1-2-i-3-n-2-smplify-B-n-1-2-3-n-1-2-3-n-n-integr-natural-

Tinku Tara 0 Comments
Pin




Question Number 49952 by maxmathsup by imad last updated on 12/Dec/18
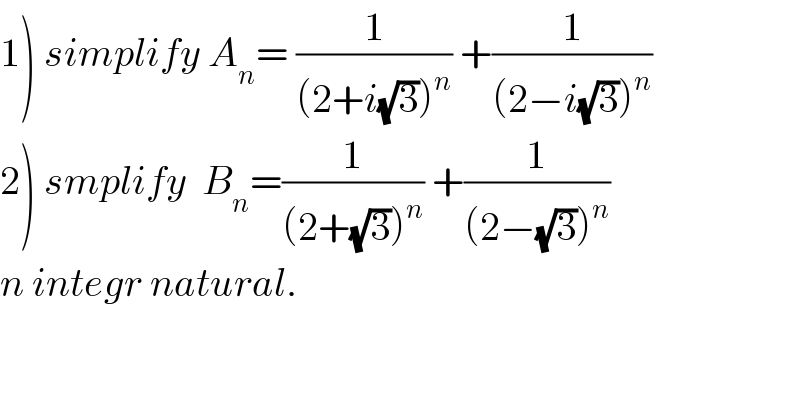
1) simplify A_n = (1/((2+i(√3))^n )) +(1/((2−i(√3))^n )) 2) smplify B_n =(1/((2+(√3))^n )) +(1/((2−(√3))^n )) n integr natural.
$$\left.\mathrm{1}\right)\:{simplify}\:{A}_{{n}} =\:\frac{\mathrm{1}}{\left(\mathrm{2}+{i}\sqrt{\mathrm{3}}\right)^{{n}} }\:+\frac{\mathrm{1}}{\left(\mathrm{2}−{i}\sqrt{\mathrm{3}}\right)^{{n}} } \\ $$$$\left.\mathrm{2}\right)\:{smplify}\:\:{B}_{{n}} =\frac{\mathrm{1}}{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{n}} }\:+\frac{\mathrm{1}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{{n}} } \\ $$$${n}\:{integr}\:{natural}. \\ $$
Commented by Abdo msup. last updated on 14/Dec/18
1) we have A_n = (((2+i(√3))^n +(2−i(√3))^n )/7^n ) =((2Re( (2+i(√3))^n ))/7^n ) but 2+i(√3)=(√7)((2/( (√7))) +((i(√3))/( (√7)))) =r e^(iθ) ⇒ r=(√7)and cosθ =(2/( (√7))) ,sinθ =((√3)/( (√7))) ⇒tanθ =((√3)/2) ⇒θ =arctan(((√3)/2)) ⇒(2+i(√3))^n =((√7))^n e^(in arctan(((√3)/2))) ⇒((2((√7))^n cos(narctan(((√3)/2))))/7^n ) = (2/(((√7))^n )) cos(n arctan(((√3)/2))).
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{A}_{{n}} =\:\frac{\left(\mathrm{2}+{i}\sqrt{\mathrm{3}}\right)^{{n}} \:+\left(\mathrm{2}−{i}\sqrt{\mathrm{3}}\right)^{{n}} }{\mathrm{7}^{{n}} } \\ $$$$=\frac{\mathrm{2}{Re}\left(\:\left(\mathrm{2}+{i}\sqrt{\mathrm{3}}\right)^{{n}} \right)}{\mathrm{7}^{{n}} }\:\:{but}\:\mathrm{2}+{i}\sqrt{\mathrm{3}}=\sqrt{\mathrm{7}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{7}}}\:+\frac{{i}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{7}}}\right)\:={r}\:{e}^{{i}\theta} \:\Rightarrow \\ $$$${r}=\sqrt{\mathrm{7}}{and}\:{cos}\theta\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{7}}}\:,{sin}\theta\:=\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{7}}}\:\Rightarrow{tan}\theta\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow\theta\:={arctan}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\left(\mathrm{2}+{i}\sqrt{\mathrm{3}}\right)^{{n}} \:=\left(\sqrt{\mathrm{7}}\right)^{{n}} \:{e}^{{in}\:{arctan}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} \:\:\:\Rightarrow\frac{\mathrm{2}\left(\sqrt{\mathrm{7}}\right)^{{n}} {cos}\left({narctan}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right)}{\mathrm{7}^{{n}} } \\ $$$$=\:\frac{\mathrm{2}}{\left(\sqrt{\mathrm{7}}\right)^{{n}} }\:{cos}\left({n}\:{arctan}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right). \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 14/Dec/18
2) we hsve B_n =(((2+(√3))^n +(2−(√3))^n )/((2^2 −((√3))^2 )^n )) = Σ_(k=0) ^n C_n ^k 2^(n−k) ((√3))^k +Σ_(k=0) ^n C_n ^k 2^(n−k) (−(√3))^k =Σ_(k=0) ^n C_n ^k { ((√3))^k +(−(√3))^k )2^(n−k) =Σ_(p=0) ^([(n/2)]) C_n ^(2p) {3^p +3^p ) 2^(n−2p) =2^(n+1) Σ_(p=0) ^([(n/2)]) ((3/4))^p C_n ^(2p)
$$\left.\mathrm{2}\right)\:{we}\:{hsve}\:{B}_{{n}} =\frac{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{n}} \:+\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{{n}} }{\left(\mathrm{2}^{\mathrm{2}} \:−\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \right)^{{n}} } \\ $$$$=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\mathrm{2}^{{n}−{k}} \:\left(\sqrt{\mathrm{3}}\right)^{{k}} \:+\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\mathrm{2}^{{n}−{k}} \left(−\sqrt{\mathrm{3}}\right)^{{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left\{\:\left(\sqrt{\mathrm{3}}\right)^{{k}} \:+\left(−\sqrt{\mathrm{3}}\right)^{{k}} \right)\mathrm{2}^{{n}−{k}} \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:{C}_{{n}} ^{\mathrm{2}{p}} \:\:\:\:\left\{\mathrm{3}^{{p}} \:+\mathrm{3}^{{p}} \right)\:\mathrm{2}^{{n}−\mathrm{2}{p}} \\ $$$$=\mathrm{2}^{{n}+\mathrm{1}} \:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{p}} {C}_{{n}} ^{\mathrm{2}{p}} \: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *