Menu Close

1-simplify-S-n-x-k-1-n-sin-2-kx-2-simplify-A-n-k-1-n-sin-2-kpi-n-

Tinku Tara 0 Comments
Pin




Question Number 39332 by abdo mathsup 649 cc last updated on 05/Jul/18
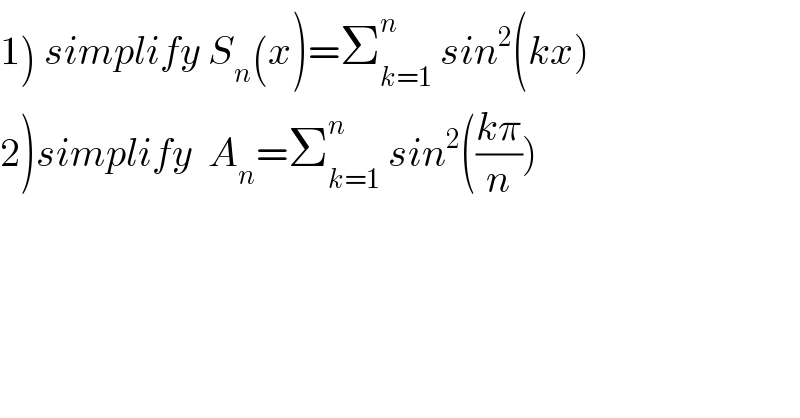
1) simplify S_n (x)=Σ_(k=1) ^n sin^2 (kx) 2)simplify A_n =Σ_(k=1) ^n sin^2 (((kπ)/n))
$$\left.\mathrm{1}\right)\:{simplify}\:{S}_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:{sin}^{\mathrm{2}} \left({kx}\right) \\ $$$$\left.\mathrm{2}\right){simplify}\:\:{A}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:{sin}^{\mathrm{2}} \left(\frac{{k}\pi}{{n}}\right) \\ $$
Commented by math khazana by abdo last updated on 09/Jul/18
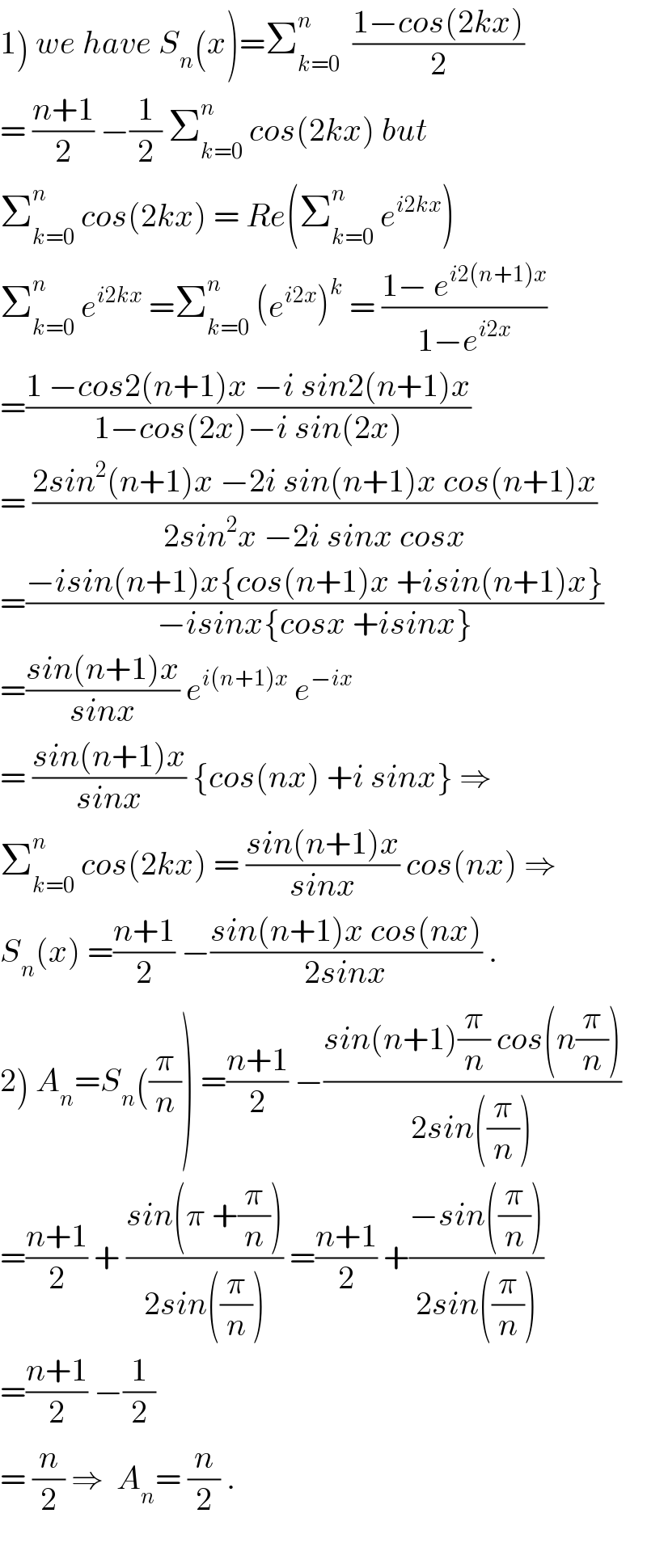
1) we have S_n (x)=Σ_(k=0) ^n ((1−cos(2kx))/2) = ((n+1)/2) −(1/2) Σ_(k=0) ^n cos(2kx) but Σ_(k=0) ^n cos(2kx) = Re(Σ_(k=0) ^n e^(i2kx) ) Σ_(k=0) ^n e^(i2kx) =Σ_(k=0) ^n (e^(i2x) )^k = ((1− e^(i2(n+1)x) )/(1−e^(i2x) )) =((1 −cos2(n+1)x −i sin2(n+1)x)/(1−cos(2x)−i sin(2x))) = ((2sin^2 (n+1)x −2i sin(n+1)x cos(n+1)x)/(2sin^2 x −2i sinx cosx)) =((−isin(n+1)x{cos(n+1)x +isin(n+1)x})/(−isinx{cosx +isinx})) =((sin(n+1)x)/(sinx)) e^(i(n+1)x) e^(−ix) = ((sin(n+1)x)/(sinx)) {cos(nx) +i sinx} ⇒ Σ_(k=0) ^n cos(2kx) = ((sin(n+1)x)/(sinx)) cos(nx) ⇒ S_n (x) =((n+1)/2) −((sin(n+1)x cos(nx))/(2sinx)) . 2) A_n =S_n ((π/n)) =((n+1)/2) −((sin(n+1)(π/n) cos(n(π/n)))/(2sin((π/n)))) =((n+1)/2) + ((sin(π +(π/n)))/(2sin((π/n)))) =((n+1)/2) +((−sin((π/n)))/(2sin((π/n)))) =((n+1)/2) −(1/2) = (n/2) ⇒ A_n = (n/2) .
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{S}_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{kx}\right)}{\mathrm{2}} \\ $$$$=\:\frac{{n}+\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\mathrm{2}{kx}\right)\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\mathrm{2}{kx}\right)\:=\:{Re}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{i}\mathrm{2}{kx}} \right) \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{i}\mathrm{2}{kx}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({e}^{{i}\mathrm{2}{x}} \right)^{{k}} \:=\:\frac{\mathrm{1}−\:{e}^{{i}\mathrm{2}\left({n}+\mathrm{1}\right){x}} }{\mathrm{1}−{e}^{{i}\mathrm{2}{x}} } \\ $$$$=\frac{\mathrm{1}\:−{cos}\mathrm{2}\left({n}+\mathrm{1}\right){x}\:−{i}\:{sin}\mathrm{2}\left({n}+\mathrm{1}\right){x}}{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)−{i}\:{sin}\left(\mathrm{2}{x}\right)} \\ $$$$=\:\frac{\mathrm{2}{sin}^{\mathrm{2}} \left({n}+\mathrm{1}\right){x}\:−\mathrm{2}{i}\:{sin}\left({n}+\mathrm{1}\right){x}\:{cos}\left({n}+\mathrm{1}\right){x}}{\mathrm{2}{sin}^{\mathrm{2}} {x}\:−\mathrm{2}{i}\:{sinx}\:{cosx}} \\ $$$$=\frac{−{isin}\left({n}+\mathrm{1}\right){x}\left\{{cos}\left({n}+\mathrm{1}\right){x}\:+{isin}\left({n}+\mathrm{1}\right){x}\right\}}{−{isinx}\left\{{cosx}\:+{isinx}\right\}} \\ $$$$=\frac{{sin}\left({n}+\mathrm{1}\right){x}}{{sinx}}\:{e}^{{i}\left({n}+\mathrm{1}\right){x}} \:{e}^{−{ix}} \\ $$$$=\:\frac{{sin}\left({n}+\mathrm{1}\right){x}}{{sinx}}\:\left\{{cos}\left({nx}\right)\:+{i}\:{sinx}\right\}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\mathrm{2}{kx}\right)\:=\:\frac{{sin}\left({n}+\mathrm{1}\right){x}}{{sinx}}\:{cos}\left({nx}\right)\:\Rightarrow \\ $$$${S}_{{n}} \left({x}\right)\:=\frac{{n}+\mathrm{1}}{\mathrm{2}}\:−\frac{{sin}\left({n}+\mathrm{1}\right){x}\:{cos}\left({nx}\right)}{\mathrm{2}{sinx}}\:. \\ $$$$\left.\mathrm{2}\right)\:{A}_{{n}} ={S}_{{n}} \left(\frac{\pi}{{n}}\right)\:=\frac{{n}+\mathrm{1}}{\mathrm{2}}\:−\frac{{sin}\left({n}+\mathrm{1}\right)\frac{\pi}{{n}}\:{cos}\left({n}\frac{\pi}{{n}}\right)}{\mathrm{2}{sin}\left(\frac{\pi}{{n}}\right)} \\ $$$$=\frac{{n}+\mathrm{1}}{\mathrm{2}}\:+\:\frac{{sin}\left(\pi\:+\frac{\pi}{{n}}\right)}{\mathrm{2}{sin}\left(\frac{\pi}{{n}}\right)}\:=\frac{{n}+\mathrm{1}}{\mathrm{2}}\:+\frac{−{sin}\left(\frac{\pi}{{n}}\right)}{\mathrm{2}{sin}\left(\frac{\pi}{{n}}\right)} \\ $$$$=\frac{{n}+\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\:\frac{{n}}{\mathrm{2}}\:\Rightarrow\:\:{A}_{{n}} =\:\frac{{n}}{\mathrm{2}}\:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *