Question Number 45836 by last updated on 17/Oct/18
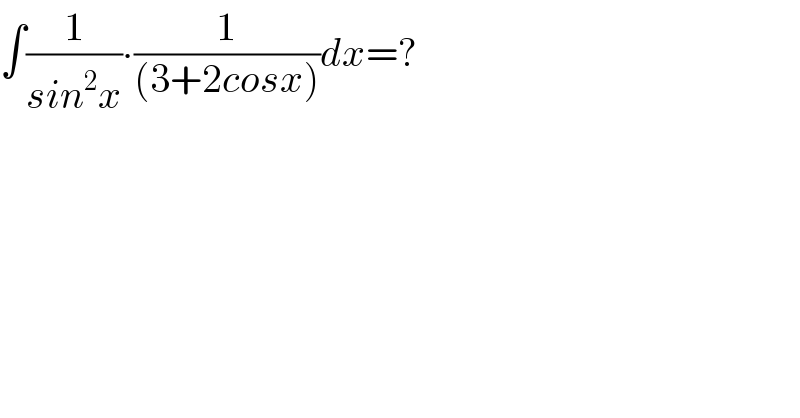
$$\int\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}}\centerdot\frac{\mathrm{1}}{\left(\mathrm{3}+\mathrm{2}{cosx}\right)}{dx}=? \\ $$
Commented by MJS last updated on 17/Oct/18

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
Commented by MJS last updated on 17/Oct/18
![Weierstrass−substitution t=tan (x/2) ⇒ sin x =((2t)/(1+t^2 )), cos x =((1−t^2 )/(1+t^2 )), dx=((2dt)/(1+t^2 )) ∫(dx/((3+2cos x)sin^2 x))=(1/2)∫(((t^2 +1)^2 )/(t^2 (t^2 +5)))dt= =(1/2)∫(1+((1−3t^2 )/(t^2 (t^2 +5))))dt=(1/2)∫dt−(1/2)∫((3t^2 −1)/(t^2 (t^2 +5)))dt= (1/2)∫dt=(t/2)=(1/2)tan (x/2) −(1/2)∫((3t^2 −1)/(t^2 (t^2 +5)))dt=(1/(10))∫((1/t^2 )−((16)/(t^2 +5)))dt= =(1/(10))∫(dt/t^2 )−(8/5)∫(dt/(t^2 +5))= (1/(10))∫(dt/t^2 )=(1/(10t))=−(1/(10))cot (x/2) −(8/5)∫(dt/(t^2 +5))= [u=((√5)/5)t → dt=du(√5)] =−((8(√5))/(25))∫(du/(u^2 +1))=−((8(√5))/(25))arctan u =−((8(√5))/(25))arctan (((√5)/5)t)= =−((8(√5))/(25))arctan (((√5)/5)tan (x/2)). ∫(dx/((3+2cos x)sin^2 x))=(1/2)tan (x/2) −(1/(10))cot (x/2) −((8(√5))/(25))arctan (((√5)/5)tan (x/2)) +C](https://www.tinkutara.com/question/Q45843.png)
$$\mathrm{Weierstrass}−\mathrm{substitution} \\ $$$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\Rightarrow\:\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} },\:\:\mathrm{cos}\:{x}\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} },\:{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\int\frac{{dx}}{\left(\mathrm{3}+\mathrm{2cos}\:{x}\right)\mathrm{sin}^{\mathrm{2}} \:{x}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{5}\right)}{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}+\frac{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{5}\right)}\right){dt}=\frac{\mathrm{1}}{\mathrm{2}}\int{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{5}\right)}{dt}= \\ $$$$ \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int{dt}=\frac{{t}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:\frac{{x}}{\mathrm{2}} \\ $$$$ \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{5}\right)}{dt}=\frac{\mathrm{1}}{\mathrm{10}}\int\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{16}}{{t}^{\mathrm{2}} +\mathrm{5}}\right){dt}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{10}}\int\frac{{dt}}{{t}^{\mathrm{2}} }−\frac{\mathrm{8}}{\mathrm{5}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{5}}= \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{10}}\int\frac{{dt}}{{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{10}{t}}=−\frac{\mathrm{1}}{\mathrm{10}}\mathrm{cot}\:\frac{{x}}{\mathrm{2}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{8}}{\mathrm{5}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{5}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}{t}\:\rightarrow\:{dt}={du}\sqrt{\mathrm{5}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{25}}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=−\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{25}}\mathrm{arctan}\:{u}\:=−\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{25}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}{t}\right)= \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{25}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right). \\ $$$$ \\ $$$$\int\frac{{dx}}{\left(\mathrm{3}+\mathrm{2cos}\:{x}\right)\mathrm{sin}^{\mathrm{2}} \:{x}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{10}}\mathrm{cot}\:\frac{{x}}{\mathrm{2}}\:−\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{25}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right)\:+{C} \\ $$
Commented by last updated on 17/Oct/18
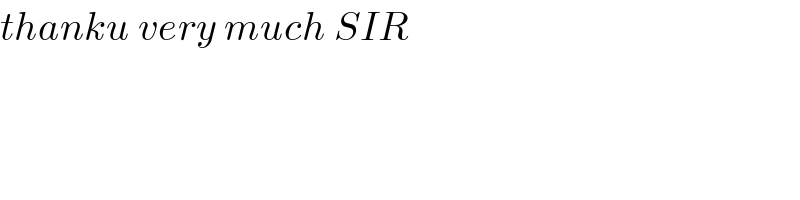
$${thanku}\:{very}\:{much}\:{SIR} \\ $$
