Question Number 14688 by tawa tawa last updated on 03/Jun/17
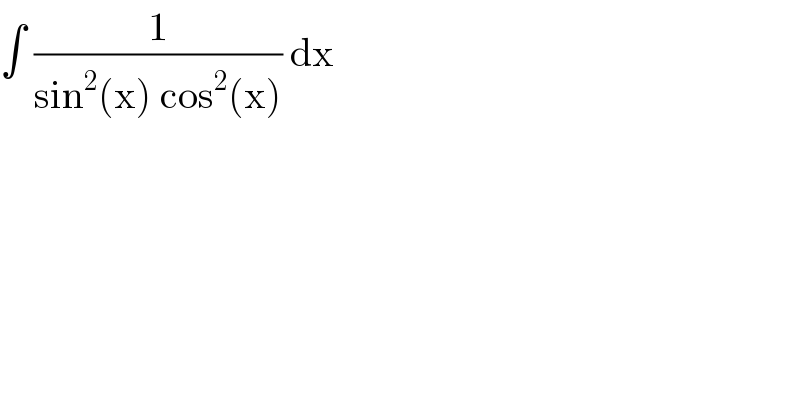
$$\int\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\:\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)}\:\mathrm{dx} \\ $$
Answered by ajfour last updated on 03/Jun/17
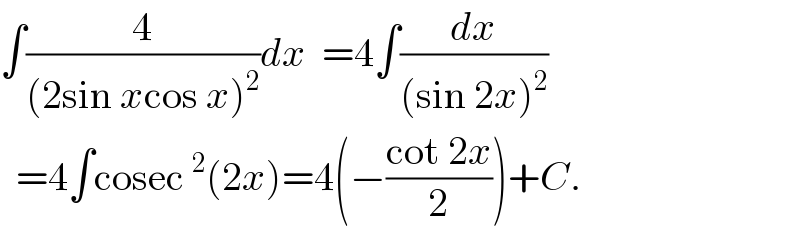
$$\int\frac{\mathrm{4}}{\left(\mathrm{2sin}\:{x}\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{dx}\:\:=\mathrm{4}\int\frac{{dx}}{\left(\mathrm{sin}\:\mathrm{2}{x}\right)^{\mathrm{2}} } \\ $$$$\:\:=\mathrm{4}\int\mathrm{cosec}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)=\mathrm{4}\left(−\frac{\mathrm{cot}\:\mathrm{2}{x}}{\mathrm{2}}\right)+{C}. \\ $$
Commented by tawa tawa last updated on 03/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17
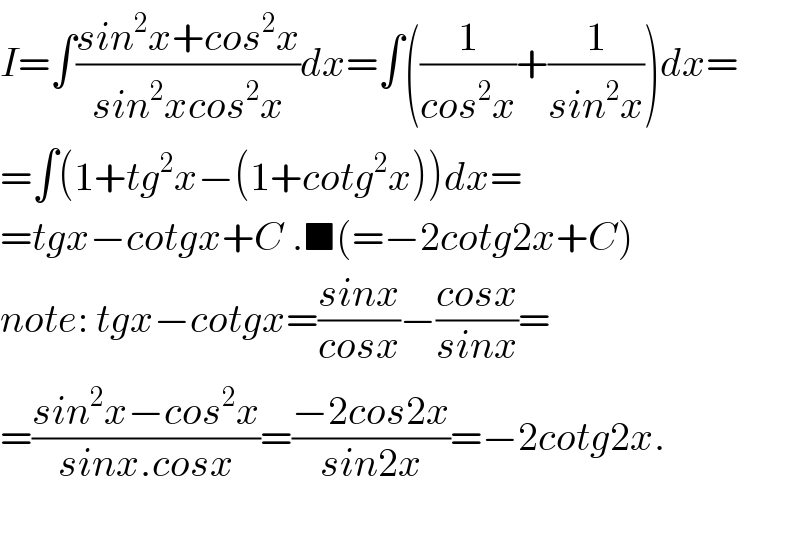
$${I}=\int\frac{{sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}}{{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}{dx}=\int\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}+\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}}\right){dx}= \\ $$$$=\int\left(\mathrm{1}+{tg}^{\mathrm{2}} {x}−\left(\mathrm{1}+{cotg}^{\mathrm{2}} {x}\right)\right){dx}= \\ $$$$={tgx}−{cotgx}+{C}\:.\blacksquare\left(=−\mathrm{2}{cotg}\mathrm{2}{x}+{C}\right) \\ $$$${note}:\:{tgx}−{cotgx}=\frac{{sinx}}{{cosx}}−\frac{{cosx}}{{sinx}}= \\ $$$$=\frac{{sin}^{\mathrm{2}} {x}−{cos}^{\mathrm{2}} {x}}{{sinx}.{cosx}}=\frac{−\mathrm{2}{cos}\mathrm{2}{x}}{{sin}\mathrm{2}{x}}=−\mathrm{2}{cotg}\mathrm{2}{x}. \\ $$$$ \\ $$
Commented by tawa tawa last updated on 03/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
