Menu Close

1-sin-2x-1-sin-2x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 168188 by cortano1 last updated on 05/Apr/22
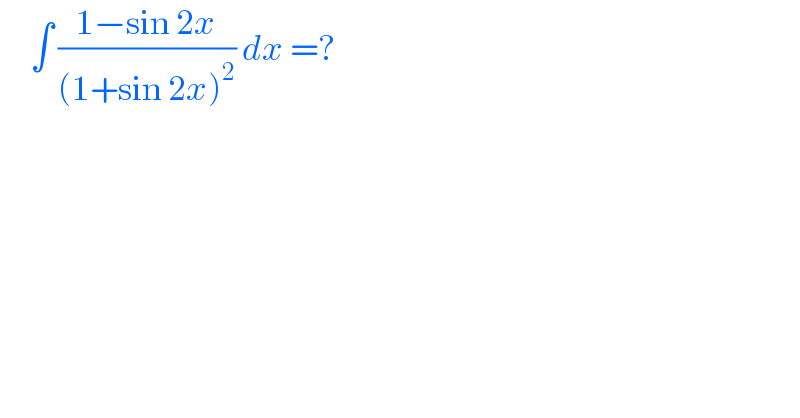
∫ ((1−sin 2x)/((1+sin 2x)^2 )) dx =?
$$\:\:\:\:\:\int\:\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}}{\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}\right)^{\mathrm{2}} }\:{dx}\:=? \\ $$
Commented by Florian last updated on 09/Apr/22
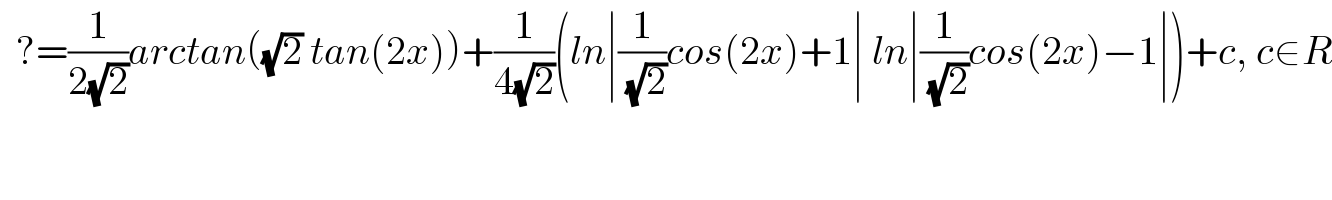
?=(1/(2(√2)))arctan((√2) tan(2x))+(1/(4(√2)))(ln∣(1/( (√2)))cos(2x)+1∣ ln∣(1/( (√2)))cos(2x)−1∣)+c, c∈R
$$\:\:?=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{arctan}\left(\sqrt{\mathrm{2}}\:{tan}\left(\mathrm{2}{x}\right)\right)+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left({ln}\mid\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}\mid\:{ln}\mid\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cos}\left(\mathrm{2}{x}\right)−\mathrm{1}\mid\right)+{c},\:{c}\in{R} \\ $$
Answered by peter frank last updated on 05/Apr/22
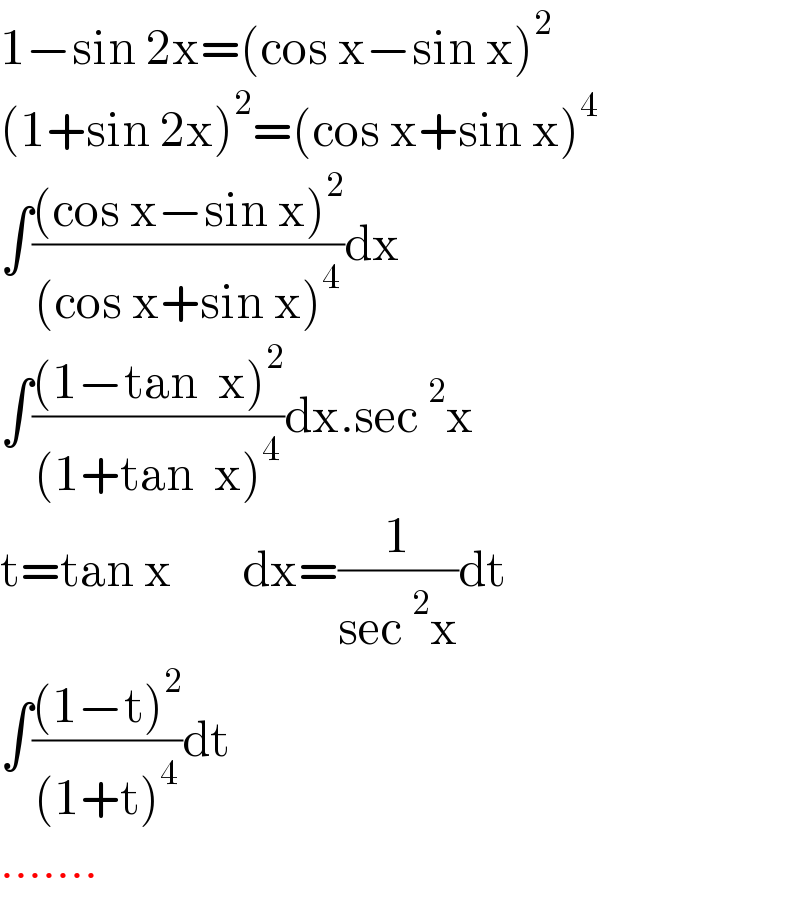
1−sin 2x=(cos x−sin x)^2 (1+sin 2x)^2 =(cos x+sin x)^4 ∫(((cos x−sin x)^2 )/((cos x+sin x)^4 ))dx ∫(((1−tan x)^2 )/((1+tan x)^4 ))dx.sec^2 x t=tan x dx=(1/(sec^2 x))dt ∫(((1−t)^2 )/((1+t)^4 ))dt .......
$$\mathrm{1}−\mathrm{sin}\:\mathrm{2x}=\left(\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2x}\right)^{\mathrm{2}} =\left(\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{4}} \\ $$$$\int\frac{\left(\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{2}} }{\left(\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{4}} }\mathrm{dx} \\ $$$$\int\frac{\left(\mathrm{1}−\mathrm{tan}\:\:\mathrm{x}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{tan}\:\:\mathrm{x}\right)^{\mathrm{4}} }\mathrm{dx}.\mathrm{sec}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{t}=\mathrm{tan}\:\mathrm{x}\:\:\:\:\:\:\:\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}\mathrm{dt} \\ $$$$\int\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{4}} }\mathrm{dt} \\ $$$$……. \\ $$
Answered by Mathspace last updated on 05/Apr/22
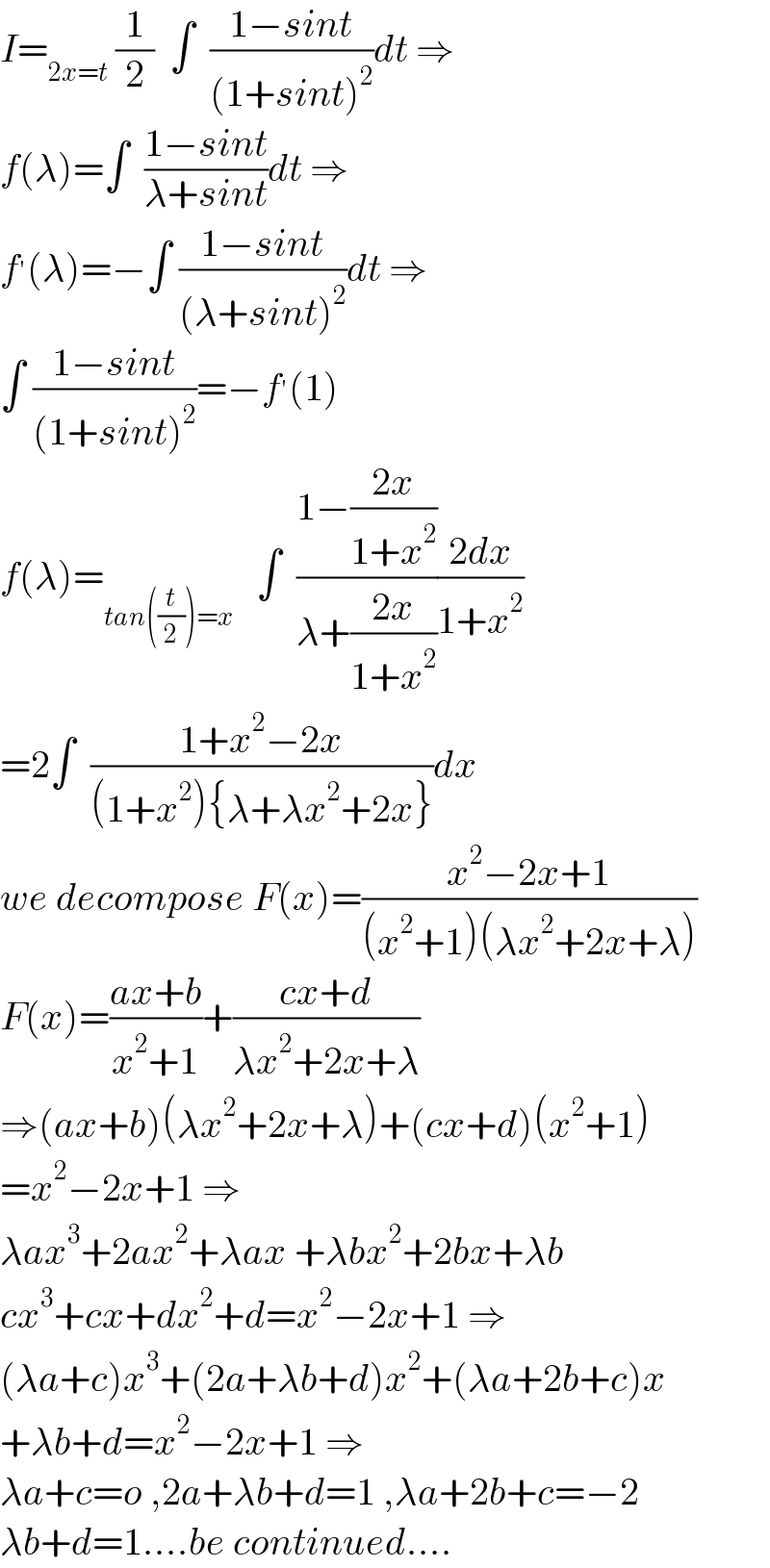
I=_(2x=t) (1/2) ∫ ((1−sint)/((1+sint)^2 ))dt ⇒ f(λ)=∫ ((1−sint)/(λ+sint))dt ⇒ f^′ (λ)=−∫ ((1−sint)/((λ+sint)^2 ))dt ⇒ ∫ ((1−sint)/((1+sint)^2 ))=−f^′ (1) f(λ)=_(tan((t/2))=x) ∫ ((1−((2x)/(1+x^2 )))/(λ+((2x)/(1+x^2 ))))((2dx)/(1+x^2 )) =2∫ ((1+x^2 −2x)/((1+x^2 ){λ+λx^2 +2x}))dx we decompose F(x)=((x^2 −2x+1)/((x^2 +1)(λx^2 +2x+λ))) F(x)=((ax+b)/(x^2 +1))+((cx+d)/(λx^2 +2x+λ)) ⇒(ax+b)(λx^2 +2x+λ)+(cx+d)(x^2 +1) =x^2 −2x+1 ⇒ λax^3 +2ax^2 +λax +λbx^2 +2bx+λb cx^3 +cx+dx^2 +d=x^2 −2x+1 ⇒ (λa+c)x^3 +(2a+λb+d)x^2 +(λa+2b+c)x +λb+d=x^2 −2x+1 ⇒ λa+c=o ,2a+λb+d=1 ,λa+2b+c=−2 λb+d=1....be continued....
$${I}=_{\mathrm{2}{x}={t}} \:\frac{\mathrm{1}}{\mathrm{2}}\:\:\int\:\:\frac{\mathrm{1}−{sint}}{\left(\mathrm{1}+{sint}\right)^{\mathrm{2}} }{dt}\:\Rightarrow \\ $$$${f}\left(\lambda\right)=\int\:\:\frac{\mathrm{1}−{sint}}{\lambda+{sint}}{dt}\:\Rightarrow \\ $$$${f}^{'} \left(\lambda\right)=−\int\:\frac{\mathrm{1}−{sint}}{\left(\lambda+{sint}\right)^{\mathrm{2}} }{dt}\:\Rightarrow \\ $$$$\int\:\frac{\mathrm{1}−{sint}}{\left(\mathrm{1}+{sint}\right)^{\mathrm{2}} }=−{f}^{'} \left(\mathrm{1}\right) \\ $$$${f}\left(\lambda\right)=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={x}} \:\:\:\int\:\:\frac{\mathrm{1}−\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }}{\lambda+\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }}\frac{\mathrm{2}{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int\:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left\{\lambda+\lambda{x}^{\mathrm{2}} +\mathrm{2}{x}\right\}}{dx} \\ $$$${we}\:{decompose}\:{F}\left({x}\right)=\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\lambda{x}^{\mathrm{2}} +\mathrm{2}{x}+\lambda\right)} \\ $$$${F}\left({x}\right)=\frac{{ax}+{b}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{{cx}+{d}}{\lambda{x}^{\mathrm{2}} +\mathrm{2}{x}+\lambda} \\ $$$$\Rightarrow\left({ax}+{b}\right)\left(\lambda{x}^{\mathrm{2}} +\mathrm{2}{x}+\lambda\right)+\left({cx}+{d}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\:\Rightarrow \\ $$$$\lambda{ax}^{\mathrm{3}} +\mathrm{2}{ax}^{\mathrm{2}} +\lambda{ax}\:+\lambda{bx}^{\mathrm{2}} +\mathrm{2}{bx}+\lambda{b} \\ $$$${cx}^{\mathrm{3}} +{cx}+{dx}^{\mathrm{2}} +{d}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\:\Rightarrow \\ $$$$\left(\lambda{a}+{c}\right){x}^{\mathrm{3}} +\left(\mathrm{2}{a}+\lambda{b}+{d}\right){x}^{\mathrm{2}} +\left(\lambda{a}+\mathrm{2}{b}+{c}\right){x} \\ $$$$+\lambda{b}+{d}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\:\Rightarrow \\ $$$$\lambda{a}+{c}={o}\:,\mathrm{2}{a}+\lambda{b}+{d}=\mathrm{1}\:,\lambda{a}+\mathrm{2}{b}+{c}=−\mathrm{2} \\ $$$$\lambda{b}+{d}=\mathrm{1}….{be}\:{continued}…. \\ $$
Answered by MJS_new last updated on 06/Apr/22
∫((1−sin 2x)/((1+sin 2x)^2 ))dx=∫((2/((1+sin 2x)^2 ))−(1/(1+sin 2x)))dx= [t=tan x → dx=(dt/(t^2 +1))] =∫(((2(t^2 +1))/((t+1)^4 ))−(1/((t+1)^2 )))dt= =∫((4/((t+1)^4 ))−(4/((t+1)^3 ))+(1/((t+1)^2 )))dt= =−(4/(3(t+1)^3 ))+(2/((t+1)^2 ))−(1/(t+1))= =−((3t^2 +1)/(3(t+1)^3 ))= =−((1+3tan^2 x)/(3(1+tan x)^3 ))+C [=−((cos^3 2x)/(6(1+sin 2x)^3 ))+C]
$$\int\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}}{\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}\right)^{\mathrm{2}} }{dx}=\int\left(\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}}\right){dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\int\left(\frac{\mathrm{2}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\left({t}+\mathrm{1}\right)^{\mathrm{4}} }−\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\right){dt}= \\ $$$$=\int\left(\frac{\mathrm{4}}{\left({t}+\mathrm{1}\right)^{\mathrm{4}} }−\frac{\mathrm{4}}{\left({t}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\right){dt}= \\ $$$$=−\frac{\mathrm{4}}{\mathrm{3}\left({t}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{2}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}+\mathrm{1}}= \\ $$$$=−\frac{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{3}\left({t}+\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$=−\frac{\mathrm{1}+\mathrm{3tan}^{\mathrm{2}} \:{x}}{\mathrm{3}\left(\mathrm{1}+\mathrm{tan}\:{x}\right)^{\mathrm{3}} }+{C} \\ $$$$\left[=−\frac{\mathrm{cos}^{\mathrm{3}} \:\mathrm{2}{x}}{\mathrm{6}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}\right)^{\mathrm{3}} }+{C}\right] \\ $$
Commented by peter frank last updated on 06/Apr/22
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by greogoury55 last updated on 06/Apr/22
T=∫ ((1−sin 2x)/((1+sin 2x)^2 )) dx [ tan x=t → { ((dx=(dt/(1+t^2 )))),((sin 2x=((2tan x)/(1+tan^2 x))=((2t)/(1+t^2 )))) :}] T=∫ ((1+t^2 −2t)/((1+t^2 +2t)^2 )) dt =∫ (((t−1)^2 )/((t+1)^4 )) dt = ∫ ((1/((t+1)^2 )) −(4/((t+1)^3 )) +(4/((t+1)^4 )))dt = −(1/(t+1)) +(2/((t+1)^2 ))−(4/(3(t+1)^3 )) + c = −(1/(1+tan x)) +(2/((1+tan x)^2 )) −(4/((1+tan x)^3 )) + c
$$\:\mathcal{T}=\int\:\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}}{\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}\right)^{\mathrm{2}} }\:{dx}\: \\ $$$$\:\left[\:\mathrm{tan}\:{x}={t}\:\rightarrow\begin{cases}{{dx}=\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }}\\{\mathrm{sin}\:\mathrm{2}{x}=\frac{\mathrm{2tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}}=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\end{cases}\right] \\ $$$$\:\mathcal{T}=\int\:\frac{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)^{\mathrm{2}} }\:{dt} \\ $$$$\:\:=\int\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{\left({t}+\mathrm{1}\right)^{\mathrm{4}} }\:{dt}\:=\:\int\:\left(\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{4}}{\left({t}+\mathrm{1}\right)^{\mathrm{3}} }\:+\frac{\mathrm{4}}{\left({t}+\mathrm{1}\right)^{\mathrm{4}} }\right){dt} \\ $$$$\:\:=\:−\frac{\mathrm{1}}{{t}+\mathrm{1}}\:+\frac{\mathrm{2}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{4}}{\mathrm{3}\left({t}+\mathrm{1}\right)^{\mathrm{3}} }\:+\:{c} \\ $$$$\:\:=\:−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}\:{x}}\:+\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{tan}\:{x}\right)^{\mathrm{2}} }\:−\frac{\mathrm{4}}{\left(\mathrm{1}+\mathrm{tan}\:{x}\right)^{\mathrm{3}} }\:+\:{c}\: \\ $$
Commented by peter frank last updated on 07/Apr/22
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *