Question Number 87854 by jagoll last updated on 06/Apr/20
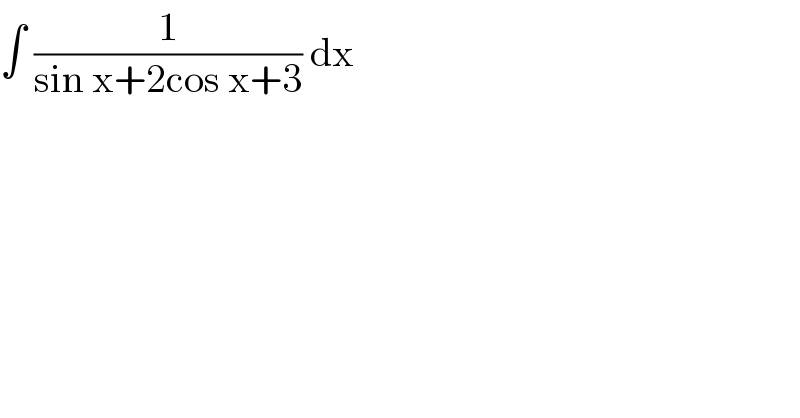
$$\int\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{x}+\mathrm{2cos}\:\mathrm{x}+\mathrm{3}}\:\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 06/Apr/20
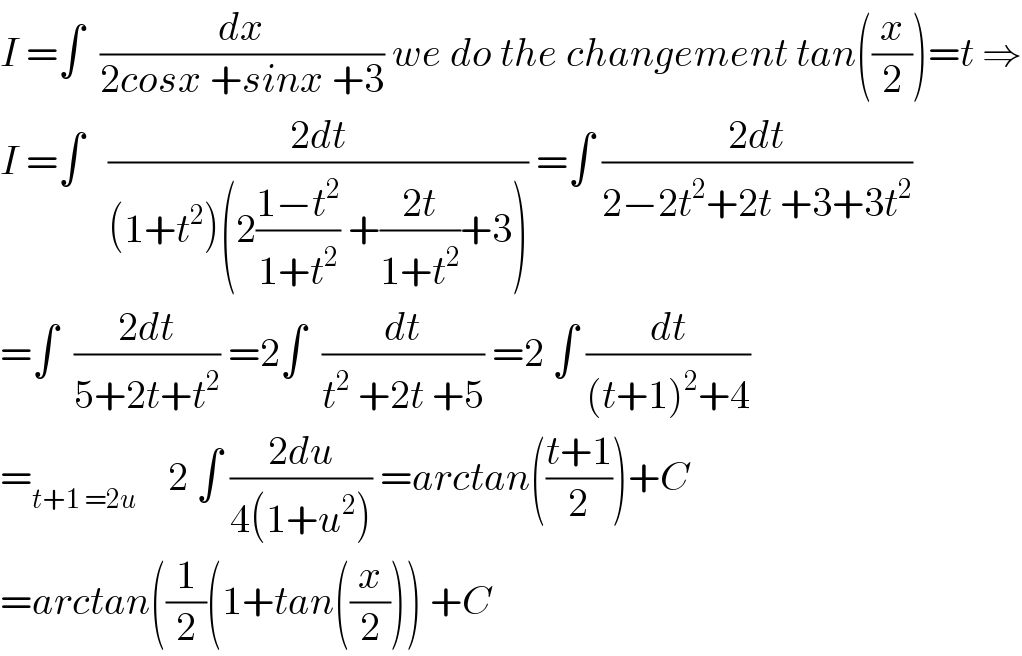
$${I}\:=\int\:\:\frac{{dx}}{\mathrm{2}{cosx}\:+{sinx}\:+\mathrm{3}}\:{we}\:{do}\:{the}\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:\Rightarrow \\ $$$${I}\:=\int\:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{2}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{3}\right)}\:=\int\:\frac{\mathrm{2}{dt}}{\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}{t}\:+\mathrm{3}+\mathrm{3}{t}^{\mathrm{2}} } \\ $$$$=\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{5}+\mathrm{2}{t}+{t}^{\mathrm{2}} }\:=\mathrm{2}\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\mathrm{5}}\:=\mathrm{2}\:\int\:\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}} \\ $$$$=_{{t}+\mathrm{1}\:=\mathrm{2}{u}} \:\:\:\:\mathrm{2}\:\int\:\frac{\mathrm{2}{du}}{\mathrm{4}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:={arctan}\left(\frac{{t}+\mathrm{1}}{\mathrm{2}}\right)+{C} \\ $$$$={arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)\:+{C}\right. \\ $$
Commented by john santu last updated on 07/Apr/20
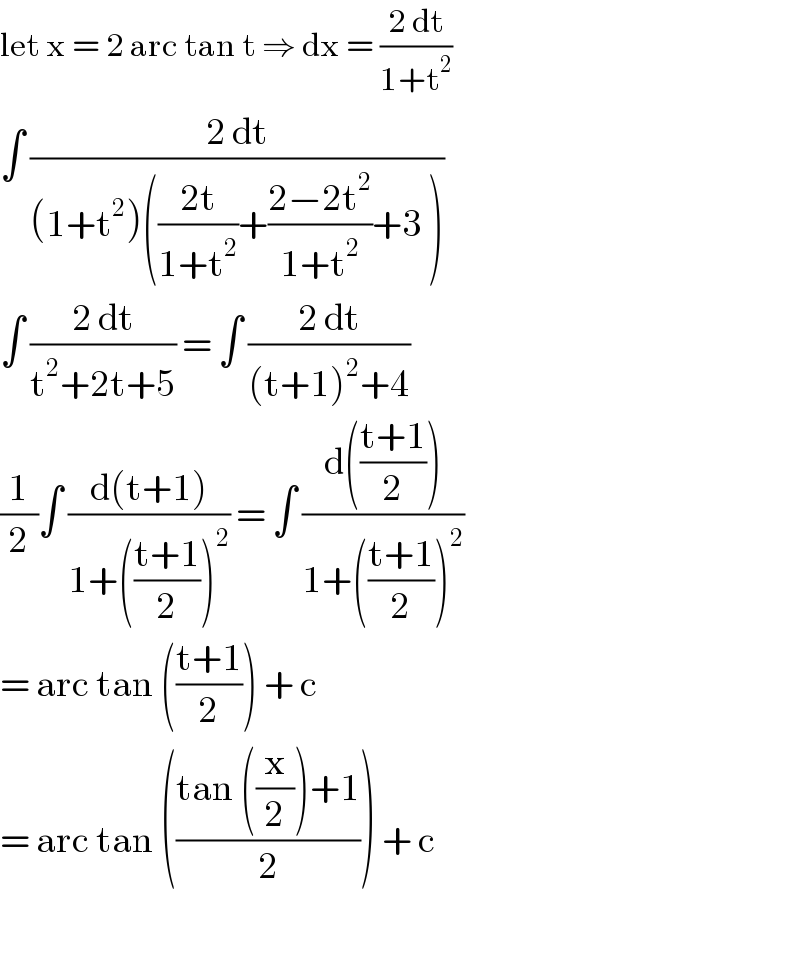
$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{2}\:\mathrm{arc}\:\mathrm{tan}\:\mathrm{t}\:\Rightarrow\:\mathrm{dx}\:=\:\frac{\mathrm{2}\:\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\int\:\frac{\mathrm{2}\:\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{2}−\mathrm{2t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\mathrm{3}\:\right)} \\ $$$$\int\:\frac{\mathrm{2}\:\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{5}}\:=\:\int\:\frac{\mathrm{2}\:\mathrm{dt}}{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{t}+\mathrm{1}\right)}{\mathrm{1}+\left(\frac{\mathrm{t}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\:\int\:\frac{\mathrm{d}\left(\frac{\mathrm{t}+\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{1}+\left(\frac{\mathrm{t}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{t}+\mathrm{1}}{\mathrm{2}}\right)\:+\:\mathrm{c} \\ $$$$=\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{tan}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{1}}{\mathrm{2}}\right)\:+\:\mathrm{c} \\ $$$$ \\ $$
Commented by jagoll last updated on 06/Apr/20

$$\mathrm{waw}…\mathrm{thanks}\:\mathrm{all} \\ $$
