Question Number 161903 by amin96 last updated on 23/Dec/21
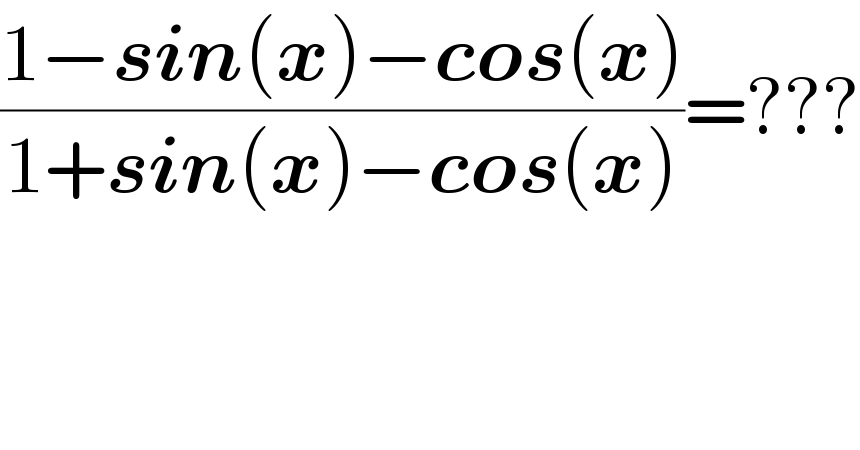
$$\frac{\mathrm{1}−\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)−\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)}{\mathrm{1}+\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)−\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)}=??? \\ $$$$ \\ $$
Commented by blackmamba last updated on 24/Dec/21
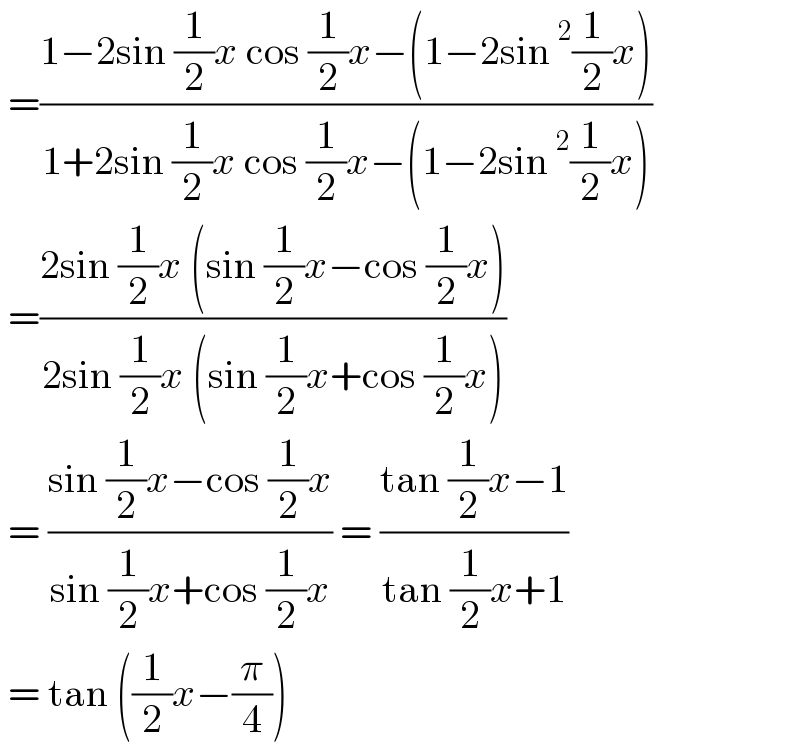
$$\:=\frac{\mathrm{1}−\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}\:\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{x}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}{x}\right)}{\mathrm{1}+\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}\:\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{x}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}{x}\right)} \\ $$$$\:=\frac{\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}\:\left(\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}−\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{x}\right)}{\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}\:\left(\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{x}\right)} \\ $$$$\:=\:\frac{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}−\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{x}}{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{x}}\:=\:\frac{\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}{x}−\mathrm{1}}{\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{1}} \\ $$$$\:=\:\mathrm{tan}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\pi}{\mathrm{4}}\right) \\ $$
Answered by MJS_new last updated on 23/Dec/21

$$\mathrm{tan}\:{x}\:−\mathrm{sec}\:{x}\:!!!!! \\ $$
Answered by Ar Brandon last updated on 24/Dec/21
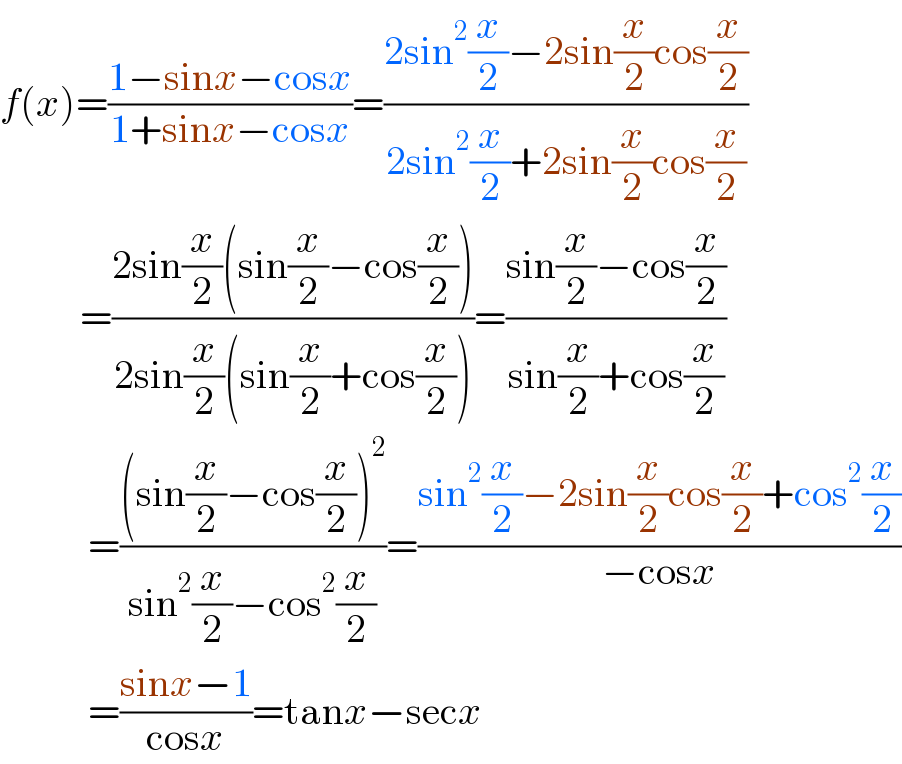
$${f}\left({x}\right)=\frac{\mathrm{1}−\mathrm{sin}{x}−\mathrm{cos}{x}}{\mathrm{1}+\mathrm{sin}{x}−\mathrm{cos}{x}}=\frac{\mathrm{2sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{2sin}\frac{{x}}{\mathrm{2}}\mathrm{cos}\frac{{x}}{\mathrm{2}}}{\mathrm{2sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{2sin}\frac{{x}}{\mathrm{2}}\mathrm{cos}\frac{{x}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2sin}\frac{{x}}{\mathrm{2}}\left(\mathrm{sin}\frac{{x}}{\mathrm{2}}−\mathrm{cos}\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2sin}\frac{{x}}{\mathrm{2}}\left(\mathrm{sin}\frac{{x}}{\mathrm{2}}+\mathrm{cos}\frac{{x}}{\mathrm{2}}\right)}=\frac{\mathrm{sin}\frac{{x}}{\mathrm{2}}−\mathrm{cos}\frac{{x}}{\mathrm{2}}}{\mathrm{sin}\frac{{x}}{\mathrm{2}}+\mathrm{cos}\frac{{x}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{sin}\frac{{x}}{\mathrm{2}}−\mathrm{cos}\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}=\frac{\mathrm{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{2sin}\frac{{x}}{\mathrm{2}}\mathrm{cos}\frac{{x}}{\mathrm{2}}+\mathrm{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{−\mathrm{cos}{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{sin}{x}−\mathrm{1}}{\mathrm{cos}{x}}=\mathrm{tan}{x}−\mathrm{sec}{x} \\ $$
Commented by peter frank last updated on 25/Dec/21

$$\mathrm{great} \\ $$
