Question Number 25777 by abhishekkumar22121999@gmail.co last updated on 14/Dec/17
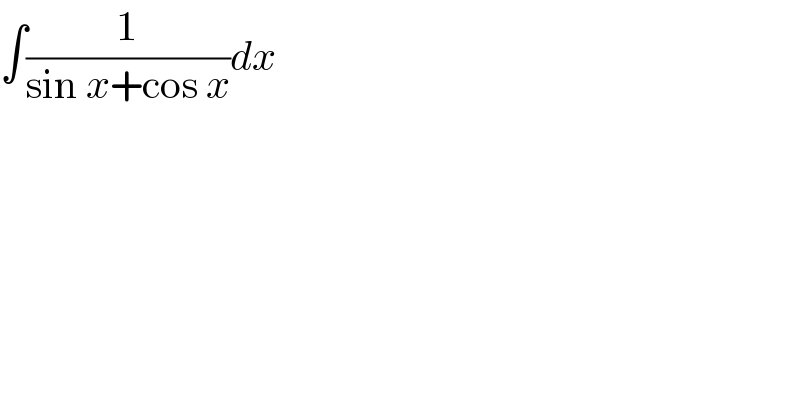
$$\int\frac{\mathrm{1}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{dx} \\ $$
Answered by mrW1 last updated on 14/Dec/17
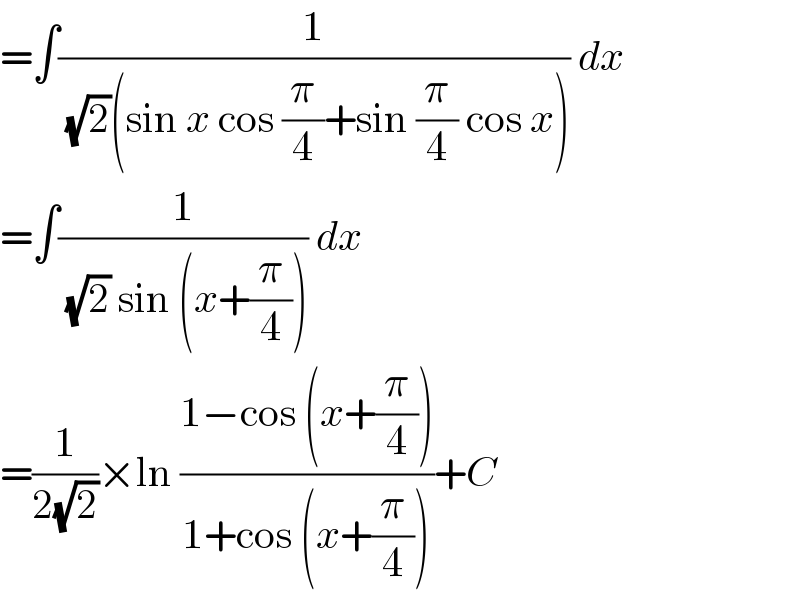
$$=\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\left(\mathrm{sin}\:{x}\:\mathrm{cos}\:\frac{\pi}{\mathrm{4}}+\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\:\mathrm{cos}\:{x}\right)}\:{dx} \\ $$$$=\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\mathrm{ln}\:\frac{\mathrm{1}−\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{1}+\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}+{C} \\ $$
