Menu Close

1-sin-x-x-

Tinku Tara 0 Comments
Pin




Question Number 122883 by kolos last updated on 20/Nov/20
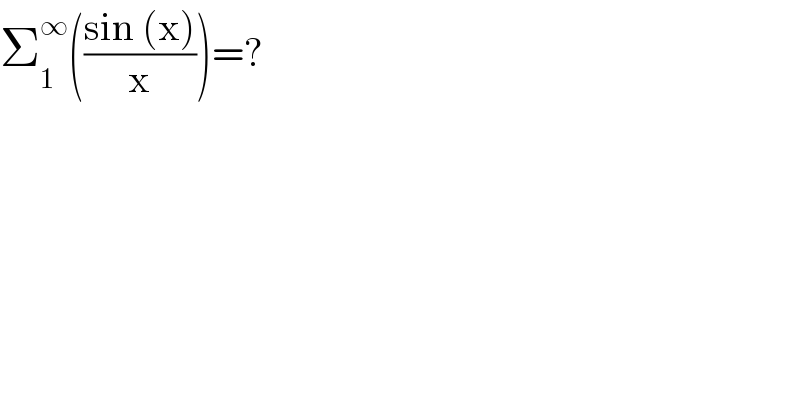
Σ_1 ^∞ (((sin (x))/x))=?
$$\sum_{\mathrm{1}} ^{\infty} \left(\frac{\mathrm{sin}\:\left(\mathrm{x}\right)}{\mathrm{x}}\right)=? \\ $$
Commented by Dwaipayan Shikari last updated on 20/Nov/20
Σ_(n=1) ^∞ ((sinx)/x)=(1/(2i))Σ_(n=1) ^∞ (e^(ix) /x)−(1/(2i))Σ^∞ (e^(−ix) /x) =(1/(2i))(−log(1−e^i )+log(1−e^(−i) ))=(1/(2i))log(((1−e^(−i) )/(1−e^i ))) =(1/(2i))log(−e^(−i) )=(1/(2i))log(e^(iπ) )+(1/(2i))(loge^(−i) )=(π/2)−(1/2)
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sinx}}{{x}}=\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{ix}} }{{x}}−\frac{\mathrm{1}}{\mathrm{2}{i}}\overset{\infty} {\sum}\frac{{e}^{−{ix}} }{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(−{log}\left(\mathrm{1}−{e}^{{i}} \right)+{log}\left(\mathrm{1}−{e}^{−{i}} \right)\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left(\frac{\mathrm{1}−{e}^{−{i}} }{\mathrm{1}−{e}^{{i}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left(−{e}^{−{i}} \right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left({e}^{{i}\pi} \right)+\frac{\mathrm{1}}{\mathrm{2}{i}}\left({loge}^{−{i}} \right)=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by kolos last updated on 21/Nov/20
thank so much , every single one
$$ \\ $$$${thank}\:{so}\:{much}\:,\:{every}\:{single}\:{one} \\ $$
Answered by TANMAY PANACEA last updated on 20/Nov/20
i think q=Σ_(x=1) ^∞ ((sinx)/x) p=Σ_(x=1) ^∞ ((cosx)/x) p+iq=Σ_(x=1) ^∞ (e^(ix) /x)=(e^i /1)+(e^(2i) /2)+(e^(3i) /3)+...∞ p+iq=−ln(1−e^i )=−ln(1−cos1−isin1) p+iq=−ln(2sin^2 (1/2)−i×2sin(1/2)xcos(1/2)) p+iq=−ln{−2sin(1/2)(sin(1/2)+icos(1/2))} p+iq=−ln{2sin(π+(1/2))(cos((π/2)−(1/2))+isin((π/2)−(1/2))} p+iaq=−ln(2sin(π+(1/2)))−ln(e^(i((π/2)−(1/2))) p+iq=−ln(2sin(π+(1/2))−i((π/2)−(1/2)) q=−(((π−1)/2)) ln(1−t)=−t−(t^2 /2)−(t^3 /3)−(t^4 /4)...∞ −ln(1−t)=t+(t^2 /2)+(t^3 /3)+..∞
$${i}\:{think} \\ $$$${q}=\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sinx}}{{x}} \\ $$$${p}=\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cosx}}{{x}} \\ $$$${p}+{iq}=\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{ix}} }{{x}}=\frac{{e}^{{i}} }{\mathrm{1}}+\frac{{e}^{\mathrm{2}{i}} }{\mathrm{2}}+\frac{{e}^{\mathrm{3}{i}} }{\mathrm{3}}+…\infty \\ $$$${p}+{iq}=−{ln}\left(\mathrm{1}−{e}^{{i}} \right)=−{ln}\left(\mathrm{1}−{cos}\mathrm{1}−{isin}\mathrm{1}\right) \\ $$$${p}+{iq}=−{ln}\left(\mathrm{2}{sin}^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}−{i}×\mathrm{2}{sin}\frac{\mathrm{1}}{\mathrm{2}}{xcos}\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${p}+{iq}=−{ln}\left\{−\mathrm{2}{sin}\frac{\mathrm{1}}{\mathrm{2}}\left({sin}\frac{\mathrm{1}}{\mathrm{2}}+{icos}\frac{\mathrm{1}}{\mathrm{2}}\right)\right\} \\ $$$${p}+{iq}=−{ln}\left\{\mathrm{2}{sin}\left(\pi+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({cos}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\right)+{isin}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right\}\right. \\ $$$${p}+{iaq}=−{ln}\left(\mathrm{2}{sin}\left(\pi+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−{ln}\left({e}^{{i}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \right. \\ $$$${p}+{iq}=−{ln}\left(\mathrm{2}{sin}\left(\pi+\frac{\mathrm{1}}{\mathrm{2}}\right)−{i}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right. \\ $$$${q}=−\left(\frac{\pi−\mathrm{1}}{\mathrm{2}}\right) \\ $$$${ln}\left(\mathrm{1}−{t}\right)=−{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\frac{{t}^{\mathrm{4}} }{\mathrm{4}}…\infty \\ $$$$−{ln}\left(\mathrm{1}−{t}\right)={t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+..\infty \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 20/Nov/20
In the same way Σ_(n=1) ^∞ ((cosx)/x)=(1/2)Σ_(n=1) ^∞ (e^(ix) /x)+(e^(−ix) /x)=(1/2)(log((1/((1−e^i )(1−e^(−i) )))) =(1/2)log((1/(1−(e^i +e^(−i) )+1)))=(1/2)log((1/(2−2cos(1))))
$${In}\:{the}\:{same}\:{way} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cosx}}{{x}}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{ix}} }{{x}}+\frac{{e}^{−{ix}} }{{x}}=\frac{\mathrm{1}}{\mathrm{2}}\left({log}\left(\frac{\mathrm{1}}{\left(\mathrm{1}−{e}^{{i}} \right)\left(\mathrm{1}−{e}^{−{i}} \right)}\right)\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}}{\mathrm{1}−\left({e}^{{i}} +{e}^{−{i}} \right)+\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}}{\mathrm{2}−\mathrm{2}{cos}\left(\mathrm{1}\right)}\right) \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 21/Nov/20
i think the Q is Σ_(n=1) ^∞ ((sin(n))/n) let S(x)=Σ_(n=1) ^∞ ((sin(nx))/n) ⇒S(x) =Im(Σ_(n=1) ^∞ (e^(inx) /n)) w(x)=Σ_(n=1) ^∞ (e^(inx) /n) ⇒w^′ (x)=Σ_(n=1) ^∞ ((in e^(inx) )/n) =iΣ_(n=1) ^∞ (e^(ix) )^n =i×(1/(1−e^(ix) )) ⇒w(x)=−ln(1−e^(ix) )+c with w)0)=0=c ⇒ w(x)=−ln(1−e^(ix) ) ⇒S(x)=Im(−ln(1−e^(ix) )) we have ln(1−e^(ix) )=ln(1−cosx−isinx) =ln(2sin^2 ((x/2))−2isin((x/2))cos((x/2))) =ln(2)+ln(−isin((x/2))(cos((x/2))+isin((x/2)))=ln(2)+ln(−i)+ln(sin((x/2)))+ln(e^((ix)/2) ) =ln(2)−((iπ)/2)+ln(sin((x/2)))+((ix)/2) =ln(2sin((x/2)))+((x−π)/2)i ⇒ S(x)=((π−x)/2) ⇒Σ_(n=1) ^∞ ((sin(n))/n) =S(1) =((π−1)/2)
$$\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{Q}\:\mathrm{is}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}} \\ $$$$\mathrm{let}\:\mathrm{S}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{nx}\right)}{\mathrm{n}}\:\Rightarrow\mathrm{S}\left(\mathrm{x}\right)\:=\mathrm{Im}\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{inx}} }{\mathrm{n}}\right) \\ $$$$\mathrm{w}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{inx}} }{\mathrm{n}}\:\Rightarrow\mathrm{w}^{'} \left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{in}\:\mathrm{e}^{\mathrm{inx}} }{\mathrm{n}}\:=\mathrm{i}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{n}} \\ $$$$\left.=\left.\mathrm{i}×\frac{\mathrm{1}}{\mathrm{1}−\mathrm{e}^{\mathrm{ix}} }\:\Rightarrow\mathrm{w}\left(\mathrm{x}\right)=−\mathrm{ln}\left(\mathrm{1}−\mathrm{e}^{\mathrm{ix}} \right)+\mathrm{c}\:\:\:\:\mathrm{with}\:\mathrm{w}\right)\mathrm{0}\right)=\mathrm{0}=\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{w}\left(\mathrm{x}\right)=−\mathrm{ln}\left(\mathrm{1}−\mathrm{e}^{\mathrm{ix}} \right)\:\Rightarrow\mathrm{S}\left(\mathrm{x}\right)=\mathrm{Im}\left(−\mathrm{ln}\left(\mathrm{1}−\mathrm{e}^{\mathrm{ix}} \right)\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{ln}\left(\mathrm{1}−\mathrm{e}^{\mathrm{ix}} \right)=\mathrm{ln}\left(\mathrm{1}−\mathrm{cosx}−\mathrm{isinx}\right)\:=\mathrm{ln}\left(\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{2isin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right) \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{ln}\left(−\mathrm{isin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\left(\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{isin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)=\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{ln}\left(−\mathrm{i}\right)+\mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)+\mathrm{ln}\left(\mathrm{e}^{\frac{\mathrm{ix}}{\mathrm{2}}} \right)\right. \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)−\frac{\mathrm{i}\pi}{\mathrm{2}}+\mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)+\frac{\mathrm{ix}}{\mathrm{2}}\:=\mathrm{ln}\left(\mathrm{2sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)+\frac{\mathrm{x}−\pi}{\mathrm{2}}\mathrm{i}\:\Rightarrow \\ $$$$\mathrm{S}\left(\mathrm{x}\right)=\frac{\pi−\mathrm{x}}{\mathrm{2}}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}}\:=\mathrm{S}\left(\mathrm{1}\right)\:=\frac{\pi−\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mnjuly1970 last updated on 21/Nov/20
Φ=Σ_(n=1) ^∞ (((sin(n))/n))=(1/(2i))Σ_(n=1) ^∞ (((e^(in) −e^(−in) )/n)) =(1/(2i))[−ln(1−e^i )+ln(1−e^(−i) )] =(1/(2i))ln(((1−e^(−i) )/(1−e^i )))=(1/(2i))ln(−e^(−i) ) =(1/(2i))[iπ−i]=((π−1)/2)
$$\:\Phi=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{{sin}\left({n}\right)}{{n}}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{{e}^{{in}} −{e}^{−{in}} }{{n}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left[−{ln}\left(\mathrm{1}−{e}^{{i}} \right)+{ln}\left(\mathrm{1}−{e}^{−{i}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}−{e}^{−{i}} }{\mathrm{1}−{e}^{{i}} }\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(−{e}^{−{i}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left[{i}\pi−{i}\right]=\frac{\pi−\mathrm{1}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *