Question Number 95524 by Abdulrahman last updated on 25/May/20

$$\frac{\mathrm{1}}{\mathrm{sin10}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{cos10}}=? \\ $$
Commented by PRITHWISH SEN 2 last updated on 25/May/20
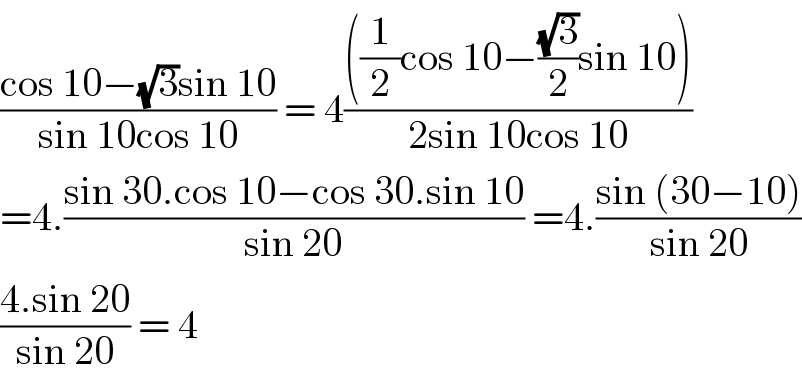
$$\frac{\mathrm{cos}\:\mathrm{10}−\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{10}}{\mathrm{sin}\:\mathrm{10cos}\:\mathrm{10}}\:=\:\mathrm{4}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{10}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:\mathrm{10}\right)}{\mathrm{2sin}\:\mathrm{10cos}\:\mathrm{10}} \\ $$$$=\mathrm{4}.\frac{\mathrm{sin}\:\mathrm{30}.\mathrm{cos}\:\mathrm{10}−\mathrm{cos}\:\mathrm{30}.\mathrm{sin}\:\mathrm{10}}{\mathrm{sin}\:\mathrm{20}}\:=\mathrm{4}.\frac{\mathrm{sin}\:\left(\mathrm{30}−\mathrm{10}\right)}{\mathrm{sin}\:\mathrm{20}} \\ $$$$\frac{\mathrm{4}.\mathrm{sin}\:\mathrm{20}}{\mathrm{sin}\:\mathrm{20}}\:=\:\mathrm{4} \\ $$
Commented by Abdulrahman last updated on 25/May/20
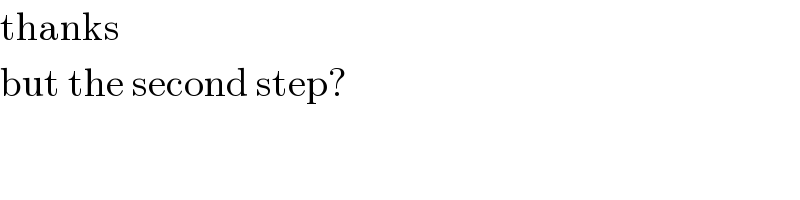
$$\mathrm{thanks}\: \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{second}\:\mathrm{step}? \\ $$$$ \\ $$
Commented by Abdulrahman last updated on 25/May/20

$$\mathrm{bundle}\:\mathrm{of}\:\mathrm{thanks} \\ $$
Commented by Tony Lin last updated on 25/May/20
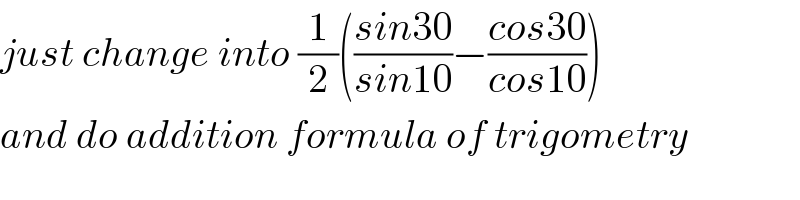
$${just}\:{change}\:{into}\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{sin}\mathrm{30}}{{sin}\mathrm{10}}−\frac{{cos}\mathrm{30}}{{cos}\mathrm{10}}\right) \\ $$$${and}\:{do}\:{addition}\:{formula}\:{of}\:{trigometry} \\ $$
