Menu Close

1-sinx-cox-1-sinx-cosx-1-cosx-1-cosx-

Tinku Tara 0 Comments
Pin




Question Number 54626 by Aditya789 last updated on 08/Feb/19
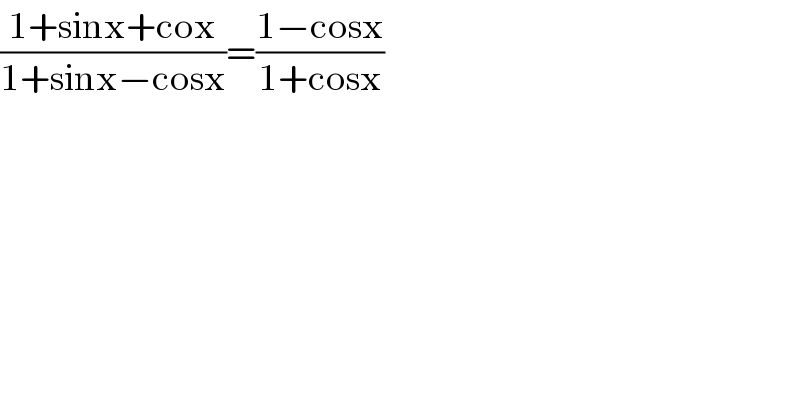
((1+sinx+cox)/(1+sinx−cosx))=((1−cosx)/(1+cosx))
$$\frac{\mathrm{1}+\mathrm{sinx}+\mathrm{cox}}{\mathrm{1}+\mathrm{sinx}−\mathrm{cosx}}=\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{1}+\mathrm{cosx}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 08/Feb/19
LHS ((2cos^2 (x/2)+2sin(x/2)cos(x/2))/(2sin^2 (x/2)+2sin(x/2)cos(x/2))) ((2cos(x/2)(cos(x/2)+sin(x/2)))/(2sin(x/2)(sin(x/2)+cos(x/(2 )))))=cot(x/2) RHS ((2sin^2 (x/2))/(2cos^2 (x/2)))=tan^2 (x/2) so pls recheck the question...
$${LHS} \\ $$$$\frac{\mathrm{2}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}}{\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{2}{cos}\frac{{x}}{\mathrm{2}}\left({cos}\frac{{x}}{\mathrm{2}}+{sin}\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}\left({sin}\frac{{x}}{\mathrm{2}}+{cos}\frac{{x}}{\mathrm{2}\:}\right)}={cot}\frac{{x}}{\mathrm{2}} \\ $$$${RHS} \\ $$$$\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{2}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}={tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}} \\ $$$${so}\:{pls}\:{recheck}\:{the}\:{question}… \\ $$
Answered by MJS last updated on 08/Feb/19
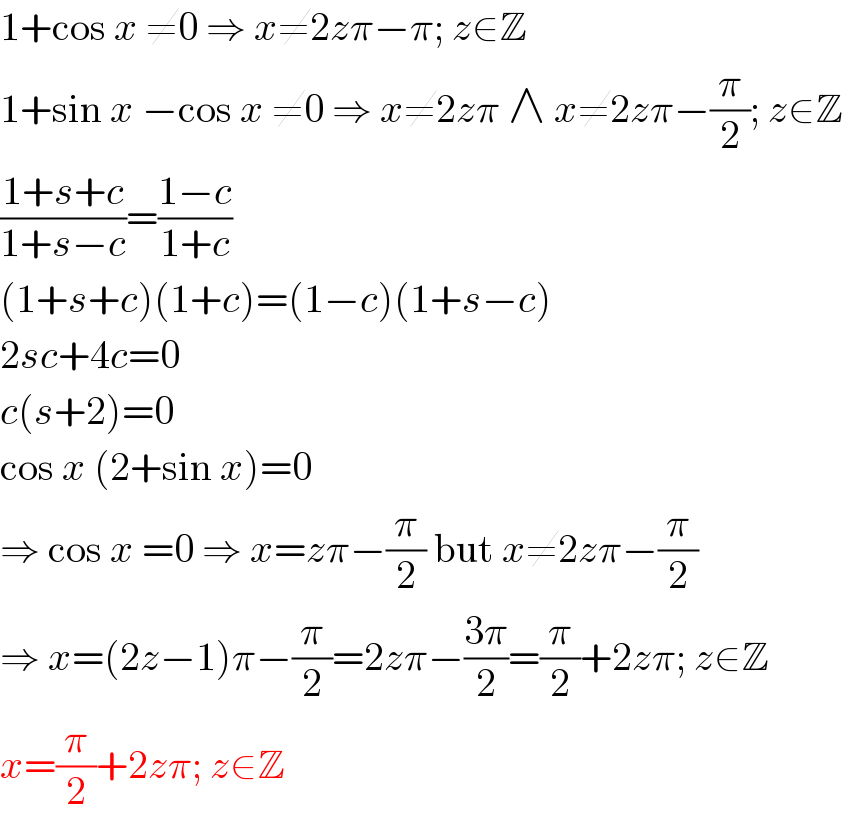
1+cos x ≠0 ⇒ x≠2zπ−π; z∈Z 1+sin x −cos x ≠0 ⇒ x≠2zπ ∧ x≠2zπ−(π/2); z∈Z ((1+s+c)/(1+s−c))=((1−c)/(1+c)) (1+s+c)(1+c)=(1−c)(1+s−c) 2sc+4c=0 c(s+2)=0 cos x (2+sin x)=0 ⇒ cos x =0 ⇒ x=zπ−(π/2) but x≠2zπ−(π/2) ⇒ x=(2z−1)π−(π/2)=2zπ−((3π)/2)=(π/2)+2zπ; z∈Z x=(π/2)+2zπ; z∈Z
$$\mathrm{1}+\mathrm{cos}\:{x}\:\neq\mathrm{0}\:\Rightarrow\:{x}\neq\mathrm{2}{z}\pi−\pi;\:{z}\in\mathbb{Z} \\ $$$$\mathrm{1}+\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}\:\neq\mathrm{0}\:\Rightarrow\:{x}\neq\mathrm{2}{z}\pi\:\wedge\:{x}\neq\mathrm{2}{z}\pi−\frac{\pi}{\mathrm{2}};\:{z}\in\mathbb{Z} \\ $$$$\frac{\mathrm{1}+{s}+{c}}{\mathrm{1}+{s}−{c}}=\frac{\mathrm{1}−{c}}{\mathrm{1}+{c}} \\ $$$$\left(\mathrm{1}+{s}+{c}\right)\left(\mathrm{1}+{c}\right)=\left(\mathrm{1}−{c}\right)\left(\mathrm{1}+{s}−{c}\right) \\ $$$$\mathrm{2}{sc}+\mathrm{4}{c}=\mathrm{0} \\ $$$${c}\left({s}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\:{x}\:\left(\mathrm{2}+\mathrm{sin}\:{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{cos}\:{x}\:=\mathrm{0}\:\Rightarrow\:{x}={z}\pi−\frac{\pi}{\mathrm{2}}\:\mathrm{but}\:{x}\neq\mathrm{2}{z}\pi−\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}=\left(\mathrm{2}{z}−\mathrm{1}\right)\pi−\frac{\pi}{\mathrm{2}}=\mathrm{2}{z}\pi−\frac{\mathrm{3}\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{2}}+\mathrm{2}{z}\pi;\:{z}\in\mathbb{Z} \\ $$$${x}=\frac{\pi}{\mathrm{2}}+\mathrm{2}{z}\pi;\:{z}\in\mathbb{Z} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *