1-sinxcos-2-x-dx-

Question Number 45688 by last updated on 15/Oct/18

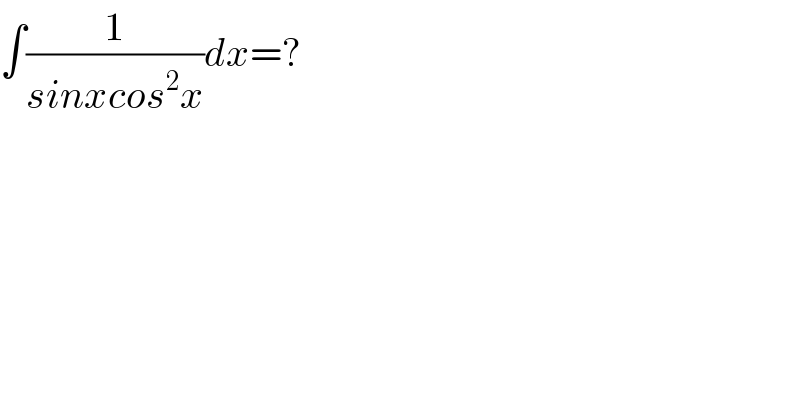
$$\int\frac{\mathrm{1}}{{sinxcos}^{\mathrm{2}} {x}}{dx}=? \\ $$

Commented by maxmathsup by imad last updated on 15/Oct/18

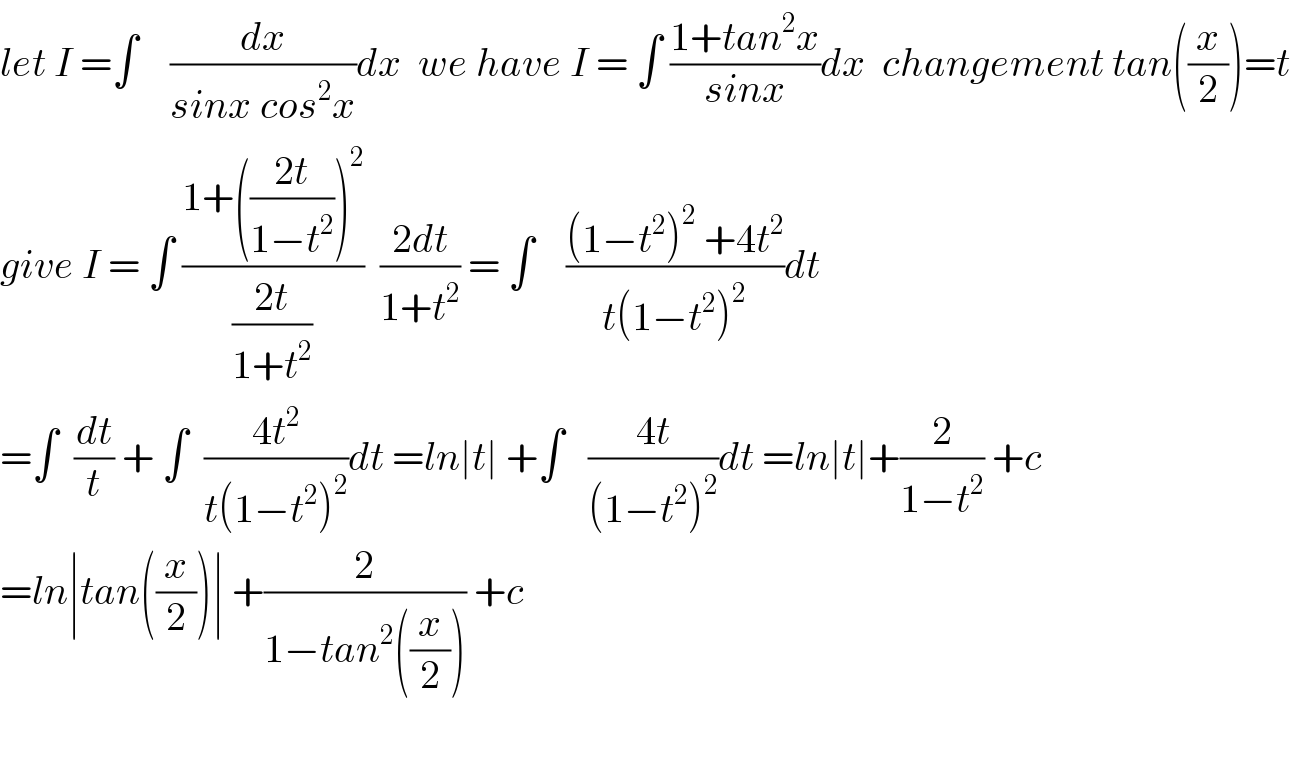
let I =∫ (dx/(sinx cos^2 x))dx we have I = ∫ ((1+tan^2 x)/(sinx))dx changement tan((x/2))=t give I = ∫ ((1+(((2t)/(1−t^2 )))^2 )/((2t)/(1+t^2 ))) ((2dt)/(1+t^2 )) = ∫ (((1−t^2 )^2 +4t^2 )/(t(1−t^2 )^2 ))dt =∫ (dt/t) + ∫ ((4t^2 )/(t(1−t^2 )^2 ))dt =ln∣t∣ +∫ ((4t)/((1−t^2 )^2 ))dt =ln∣t∣+(2/(1−t^2 )) +c =ln∣tan((x/2))∣ +(2/(1−tan^2 ((x/2)))) +c

$${let}\:{I}\:=\int\:\:\:\:\frac{{dx}}{{sinx}\:{cos}^{\mathrm{2}} {x}}{dx}\:\:{we}\:{have}\:{I}\:=\:\int\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} {x}}{{sinx}}{dx}\:\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t} \\ $$$${give}\:{I}\:=\:\int\:\frac{\mathrm{1}+\left(\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\int\:\:\:\:\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{4}{t}^{\mathrm{2}} }{{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\int\:\:\frac{{dt}}{{t}}\:+\:\int\:\:\frac{\mathrm{4}{t}^{\mathrm{2}} }{{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:={ln}\mid{t}\mid\:+\int\:\:\:\frac{\mathrm{4}{t}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:={ln}\mid{t}\mid+\frac{\mathrm{2}}{\mathrm{1}−{t}^{\mathrm{2}} }\:+{c} \\ $$$$={ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid\:+\frac{\mathrm{2}}{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\:+{c} \\ $$$$ \\ $$

Commented by last updated on 16/Oct/18

$${Thanku}\:{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18

∫((sinx)/((1−cos^2 x)cos^2 x))dx t=cosx dt=−sinxdx ∫((−dt)/(t^2 (1−t^2 ))) ∫(((1−t^2 )−t^2 )/(t^2 (1−t^2 )))dt ∫(dt/t^2 )−∫(dt/(1−t^2 )) ∫(dt/t^2 )−(1/2)∫((1+t+1−t)/((1+t)(1−t)))dt ∫t^(−2) dt−(1/2)[∫(dt/(1−t))+∫(dt/(1+t))] ∫t^(−2) dt+(1/2)∫(dt/(t−1))−(1/2)∫(dt/(t+1)) (t^(−2+1) /(−2+1))+(1/2)ln(t−1)−(1/2)ln(t+1)+c =((−1)/t)+(1/2)[ln(((t−1)/(t+1)))]+c =((−1)/(cosx))+(1/2)ln(((cosx−1)/(cosx+1)))+c

$$\int\frac{{sinx}}{\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){cos}^{\mathrm{2}} {x}}{dx} \\ $$$${t}={cosx}\:\:\:{dt}=−{sinxdx} \\ $$$$\int\frac{−{dt}}{{t}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)} \\ $$$$\int\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)−{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{dt} \\ $$$$\int\frac{{dt}}{{t}^{\mathrm{2}} }−\int\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\int\frac{{dt}}{{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+{t}+\mathrm{1}−{t}}{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}−{t}\right)}{dt} \\ $$$$\int{t}^{−\mathrm{2}} {dt}−\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{{dt}}{\mathrm{1}−{t}}+\int\frac{{dt}}{\mathrm{1}+{t}}\right] \\ $$$$\int{t}^{−\mathrm{2}} {dt}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}+\mathrm{1}} \\ $$$$\frac{{t}^{−\mathrm{2}+\mathrm{1}} }{−\mathrm{2}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}+\mathrm{1}\right)+{c} \\ $$$$=\frac{−\mathrm{1}}{{t}}+\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left(\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\right)\right]+{c} \\ $$$$=\frac{−\mathrm{1}}{{cosx}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{cosx}−\mathrm{1}}{{cosx}+\mathrm{1}}\right)+{c} \\ $$$$ \\ $$

Commented by last updated on 16/Oct/18

$${Thanku}\:{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply