Question Number 107729 by M±th+et+s last updated on 12/Aug/20
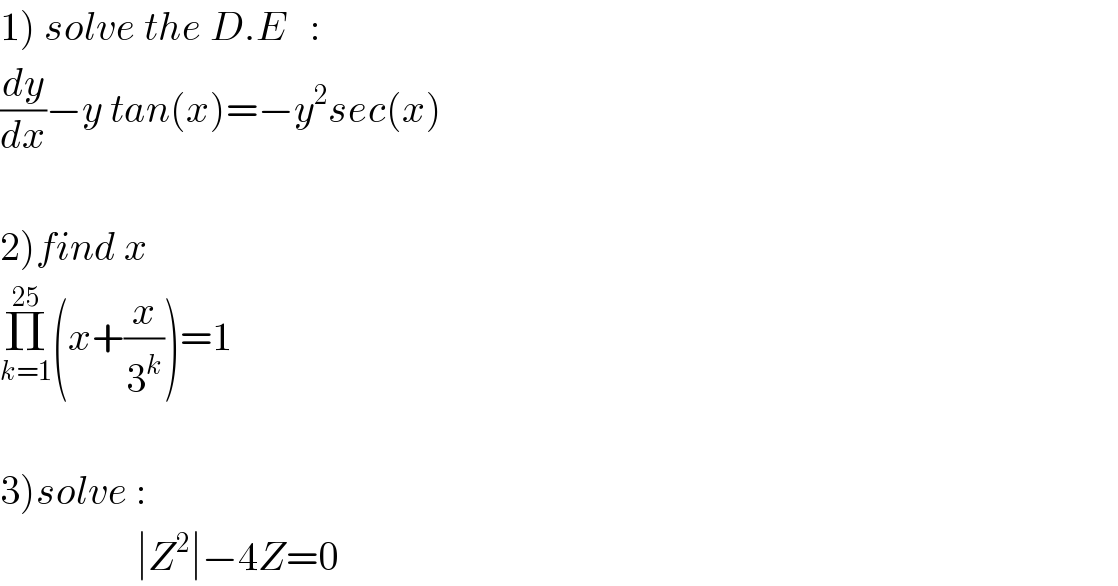
$$\left.\mathrm{1}\right)\:{solve}\:{the}\:{D}.{E}\:\:\:: \\ $$$$\frac{{dy}}{{dx}}−{y}\:{tan}\left({x}\right)=−{y}^{\mathrm{2}} {sec}\left({x}\right)\: \\ $$$$ \\ $$$$\left.\mathrm{2}\right){find}\:{x} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{25}} {\prod}}\left({x}+\frac{{x}}{\mathrm{3}^{{k}} }\right)=\mathrm{1} \\ $$$$ \\ $$$$\left.\mathrm{3}\right){solve}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{Z}^{\mathrm{2}} \mid−\mathrm{4}{Z}=\mathrm{0} \\ $$
Commented by mohammad17 last updated on 12/Aug/20

$$ \\ $$$$\left.\mathrm{1}\right)\:{y}^{−\mathrm{2}} \:\frac{{dy}}{{dx}}−{y}^{−\mathrm{1}} {tanx}=−{secx} \\ $$$$ \\ $$$${let}:\:{y}^{−\mathrm{1}} ={w}\Rightarrow−{y}^{−\mathrm{2}} \:\frac{{dy}}{{dx}}=\frac{{dw}}{{dx}} \\ $$$$ \\ $$$$\frac{{dw}}{{dx}}+{wtanx}={secx}\Rightarrow{p}\left({x}\right)={tanx},{Q}\left({x}\right)={secx} \\ $$$$ \\ $$$$\left({I}.{f}\right)={e}^{\int{p}\left({x}\right){dx}} ={e}^{\int{tanx}\:{dx}} \:={e}^{−{ln}\mid{sinx}\mid} =\frac{\mathrm{1}}{{sinx}} \\ $$$$ \\ $$$${w}=\frac{\int\left({I}.{f}\right){Q}\left({x}\right)\:{dx}}{\left({I}.{f}\right)}\Rightarrow{w}=\frac{\int{secx}\:{cscx}\:{dx}}{{cscx}} \\ $$$$ \\ $$$${w}=\frac{\mathrm{2}\int{csc}\mathrm{2}{x}\:×\frac{{csc}\mathrm{2}{x}+{cot}\mathrm{2}{x}}{{csc}\mathrm{2}{x}+{cot}\mathrm{2}{x}}\:{dx}}{{cscx}}\Rightarrow{w}=\frac{\mathrm{2}\int\frac{{csc}^{\mathrm{2}} \mathrm{2}{x}+{csc}\mathrm{2}{xcot}\mathrm{2}{x}}{{csc}\mathrm{2}{x}+{cot}\mathrm{2}{x}}{dx}}{{csc}\mathrm{2}{x}} \\ $$$$ \\ $$$${w}=\frac{−{ln}\mid{csc}\mathrm{2}{x}+{cot}\mathrm{2}{x}\mid+{c}}{{csc}\mathrm{2}{x}}\Rightarrow\frac{\mathrm{1}}{{y}}=\frac{−{ln}\mid{csc}\mathrm{2}{x}+{cot}\mathrm{2}{x}\mid+{c}}{{csc}\mathrm{2}{x}} \\ $$$$ \\ $$$${y}=\frac{{csc}\mathrm{2}{x}}{{c}−{ln}\mid{csc}\mathrm{2}{x}+{cot}\mathrm{2}{x}\mid} \\ $$$$ \\ $$$${by}:{mss}.{mohammad} \\ $$
Commented by Dwaipayan Shikari last updated on 12/Aug/20
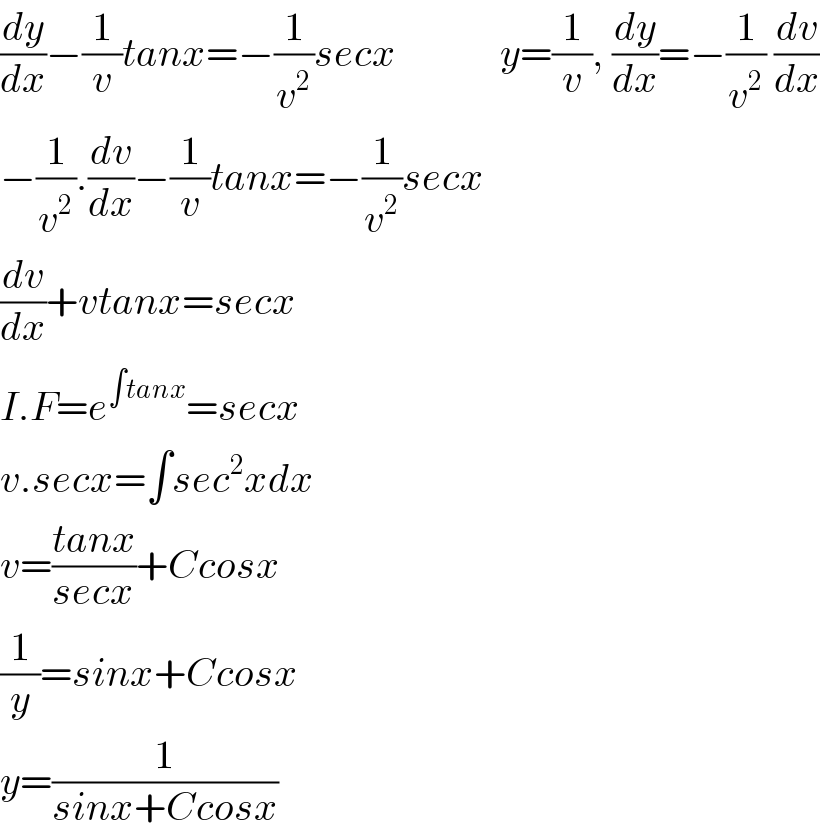
$$\frac{{dy}}{{dx}}−\frac{\mathrm{1}}{{v}}{tanx}=−\frac{\mathrm{1}}{{v}^{\mathrm{2}} }{secx}\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\frac{\mathrm{1}}{{v}},\:\frac{{dy}}{{dx}}=−\frac{\mathrm{1}}{{v}^{\mathrm{2}} }\:\frac{{dv}}{{dx}} \\ $$$$−\frac{\mathrm{1}}{{v}^{\mathrm{2}} }.\frac{{dv}}{{dx}}−\frac{\mathrm{1}}{{v}}{tanx}=−\frac{\mathrm{1}}{{v}^{\mathrm{2}} }{secx} \\ $$$$\frac{{dv}}{{dx}}+{vtanx}={secx} \\ $$$${I}.{F}={e}^{\int{tanx}} ={secx} \\ $$$${v}.{secx}=\int{sec}^{\mathrm{2}} {xdx} \\ $$$${v}=\frac{{tanx}}{{secx}}+{Ccosx} \\ $$$$\frac{\mathrm{1}}{{y}}={sinx}+{Ccosx} \\ $$$${y}=\frac{\mathrm{1}}{{sinx}+{Ccosx}} \\ $$
Commented by Dwaipayan Shikari last updated on 12/Aug/20
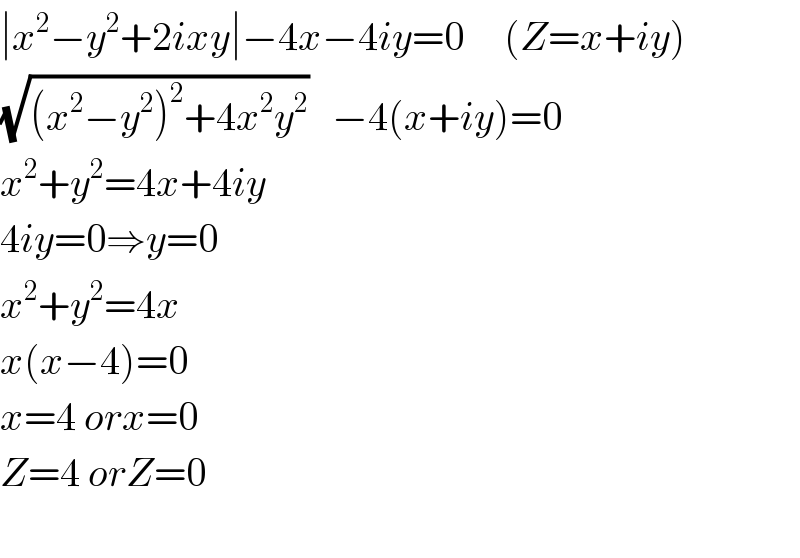
$$\mid{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{ixy}\mid−\mathrm{4}{x}−\mathrm{4}{iy}=\mathrm{0}\:\:\:\:\:\left({Z}={x}+{iy}\right) \\ $$$$\sqrt{\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} }\:\:\:−\mathrm{4}\left({x}+{iy}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}{x}+\mathrm{4}{iy} \\ $$$$\mathrm{4}{iy}=\mathrm{0}\Rightarrow{y}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}{x} \\ $$$${x}\left({x}−\mathrm{4}\right)=\mathrm{0} \\ $$$${x}=\mathrm{4}\:{orx}=\mathrm{0} \\ $$$${Z}=\mathrm{4}\:{orZ}=\mathrm{0} \\ $$$$ \\ $$
Answered by Her_Majesty last updated on 12/Aug/20
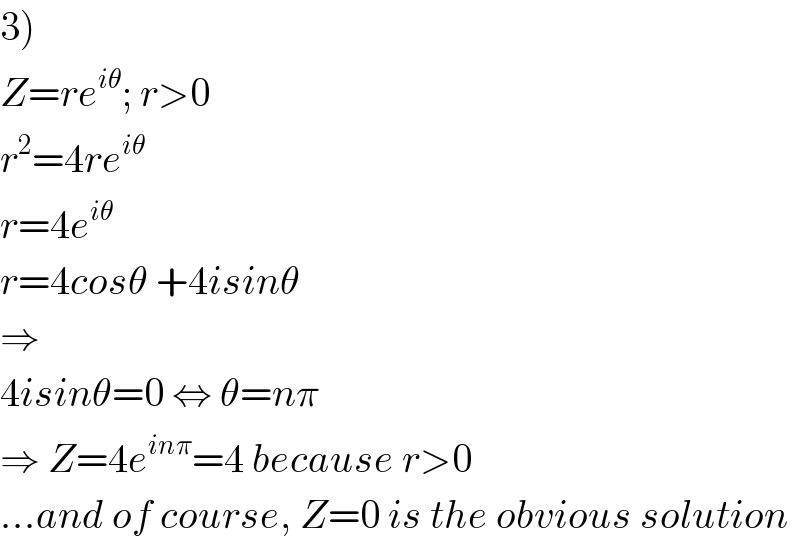
$$\left.\mathrm{3}\right) \\ $$$${Z}={re}^{{i}\theta} ;\:{r}>\mathrm{0} \\ $$$${r}^{\mathrm{2}} =\mathrm{4}{re}^{{i}\theta} \\ $$$${r}=\mathrm{4}{e}^{{i}\theta} \\ $$$${r}=\mathrm{4}{cos}\theta\:+\mathrm{4}{isin}\theta \\ $$$$\Rightarrow \\ $$$$\mathrm{4}{isin}\theta=\mathrm{0}\:\Leftrightarrow\:\theta={n}\pi \\ $$$$\Rightarrow\:{Z}=\mathrm{4}{e}^{{in}\pi} =\mathrm{4}\:{because}\:{r}>\mathrm{0} \\ $$$$…{and}\:{of}\:{course},\:{Z}=\mathrm{0}\:{is}\:{the}\:{obvious}\:{solution} \\ $$
Commented by M±th+et+s last updated on 12/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Answered by abdomathmax last updated on 12/Aug/20
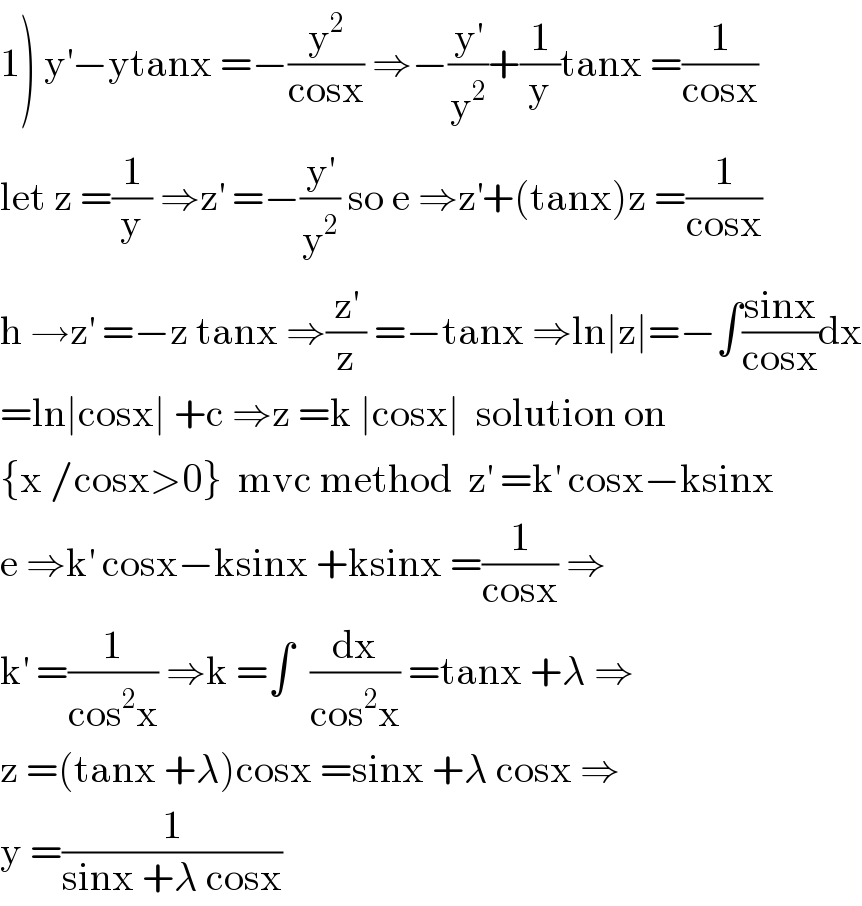
$$\left.\mathrm{1}\right)\:\mathrm{y}^{'} −\mathrm{ytanx}\:=−\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{cosx}}\:\Rightarrow−\frac{\mathrm{y}^{'} }{\mathrm{y}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{y}}\mathrm{tanx}\:=\frac{\mathrm{1}}{\mathrm{cosx}} \\ $$$$\mathrm{let}\:\mathrm{z}\:=\frac{\mathrm{1}}{\mathrm{y}}\:\Rightarrow\mathrm{z}^{'} \:=−\frac{\mathrm{y}^{'} }{\mathrm{y}^{\mathrm{2}} }\:\mathrm{so}\:\mathrm{e}\:\Rightarrow\mathrm{z}^{'} +\left(\mathrm{tanx}\right)\mathrm{z}\:=\frac{\mathrm{1}}{\mathrm{cosx}} \\ $$$$\mathrm{h}\:\rightarrow\mathrm{z}^{'} \:=−\mathrm{z}\:\mathrm{tanx}\:\Rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}\:=−\mathrm{tanx}\:\Rightarrow\mathrm{ln}\mid\mathrm{z}\mid=−\int\frac{\mathrm{sinx}}{\mathrm{cosx}}\mathrm{dx} \\ $$$$=\mathrm{ln}\mid\mathrm{cosx}\mid\:+\mathrm{c}\:\Rightarrow\mathrm{z}\:=\mathrm{k}\:\mid\mathrm{cosx}\mid\:\:\mathrm{solution}\:\mathrm{on} \\ $$$$\left\{\mathrm{x}\:/\mathrm{cosx}>\mathrm{0}\right\}\:\:\mathrm{mvc}\:\mathrm{method}\:\:\mathrm{z}^{'} \:=\mathrm{k}^{'} \:\mathrm{cosx}−\mathrm{ksinx} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{k}^{'} \:\mathrm{cosx}−\mathrm{ksinx}\:+\mathrm{ksinx}\:=\frac{\mathrm{1}}{\mathrm{cosx}}\:\Rightarrow \\ $$$$\mathrm{k}^{'} \:=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow\mathrm{k}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:=\mathrm{tanx}\:+\lambda\:\Rightarrow \\ $$$$\mathrm{z}\:=\left(\mathrm{tanx}\:+\lambda\right)\mathrm{cosx}\:=\mathrm{sinx}\:+\lambda\:\mathrm{cosx}\:\Rightarrow \\ $$$$\mathrm{y}\:=\frac{\mathrm{1}}{\mathrm{sinx}\:+\lambda\:\mathrm{cosx}} \\ $$
Commented by M±th+et+s last updated on 12/Aug/20

$${well}\:{done}\:{sir} \\ $$
Commented by abdomathmax last updated on 12/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Commented by Ar Brandon last updated on 12/Aug/20
Est-ce la méthode de variation de constante, monsieur ?��
Commented by abdomathmax last updated on 12/Aug/20

$$\mathrm{oui} \\ $$
Commented by Ar Brandon last updated on 12/Aug/20
OK��
Commented by mohammad17 last updated on 12/Aug/20
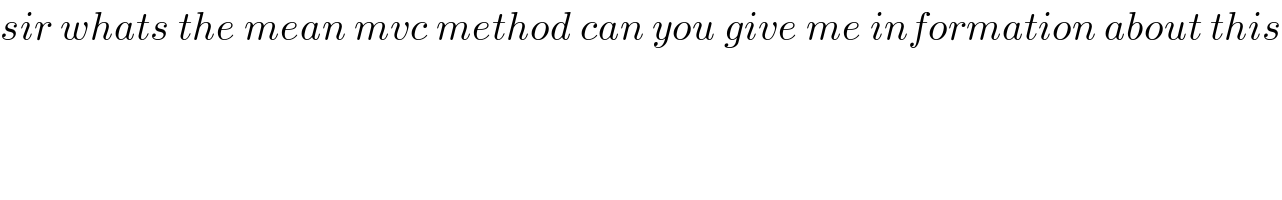
$${sir}\:{whats}\:{the}\:{mean}\:{mvc}\:{method}\:{can}\:{you}\:{give}\:{me}\:{information}\:{about}\:{this} \\ $$
Commented by Ar Brandon last updated on 12/Aug/20
It means variation of parameters in English.
Commented by mathmax by abdo last updated on 12/Aug/20

$$\mathrm{yes} \\ $$
Commented by Ar Brandon last updated on 12/Aug/20
I would like to master the mvc and the wronskian method. But I haven't found any reliable document concerning these subjects. Can someone please help me ? ��
Commented by Ar Brandon last updated on 12/Aug/20
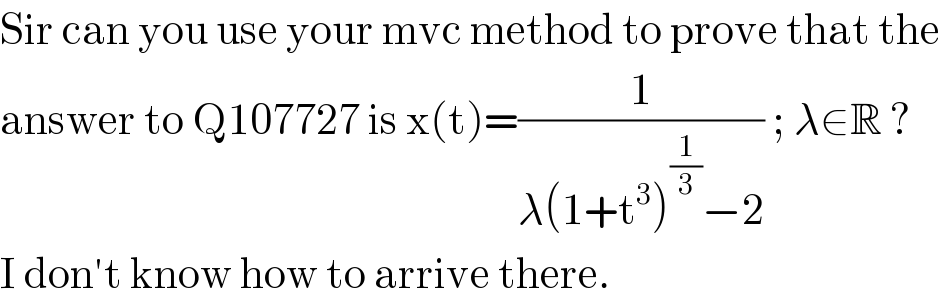
$$\mathrm{Sir}\:\mathrm{can}\:\mathrm{you}\:\mathrm{use}\:\mathrm{your}\:\mathrm{mvc}\:\mathrm{method}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{answer}\:\mathrm{to}\:\mathrm{Q107727}\:\mathrm{is}\:\mathrm{x}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\lambda\left(\mathrm{1}+\mathrm{t}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{2}}\:;\:\lambda\in\mathbb{R}\:? \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{arrive}\:\mathrm{there}. \\ $$
Answered by abdomathmax last updated on 12/Aug/20
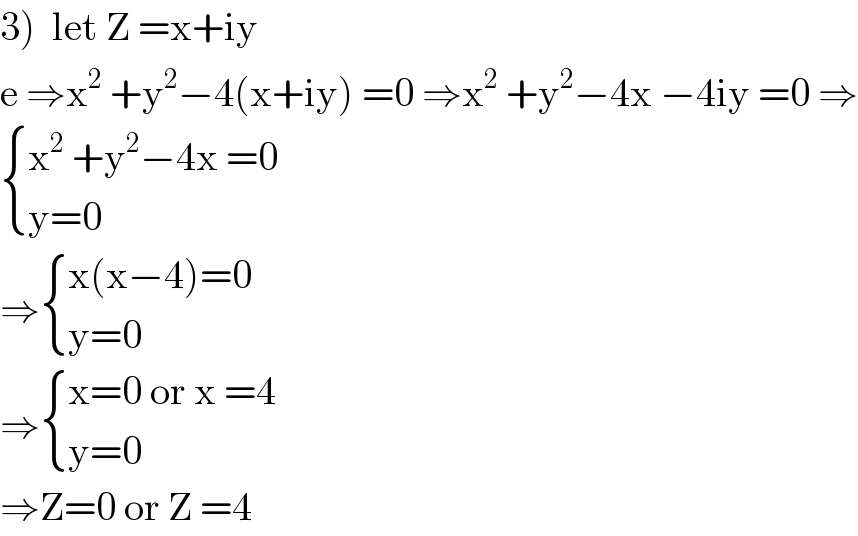
$$\left.\mathrm{3}\right)\:\:\mathrm{let}\:\mathrm{Z}\:=\mathrm{x}+\mathrm{iy}\: \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{x}+\mathrm{iy}\right)\:=\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} −\mathrm{4x}\:−\mathrm{4iy}\:=\mathrm{0}\:\Rightarrow \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} −\mathrm{4x}\:=\mathrm{0}}\\{\mathrm{y}=\mathrm{0}\:}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)=\mathrm{0}}\\{\mathrm{y}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{0}\:\mathrm{or}\:\mathrm{x}\:=\mathrm{4}}\\{\mathrm{y}=\mathrm{0}\:}\end{cases} \\ $$$$\Rightarrow\mathrm{Z}=\mathrm{0}\:\mathrm{or}\:\mathrm{Z}\:=\mathrm{4} \\ $$
Answered by bemath last updated on 12/Aug/20
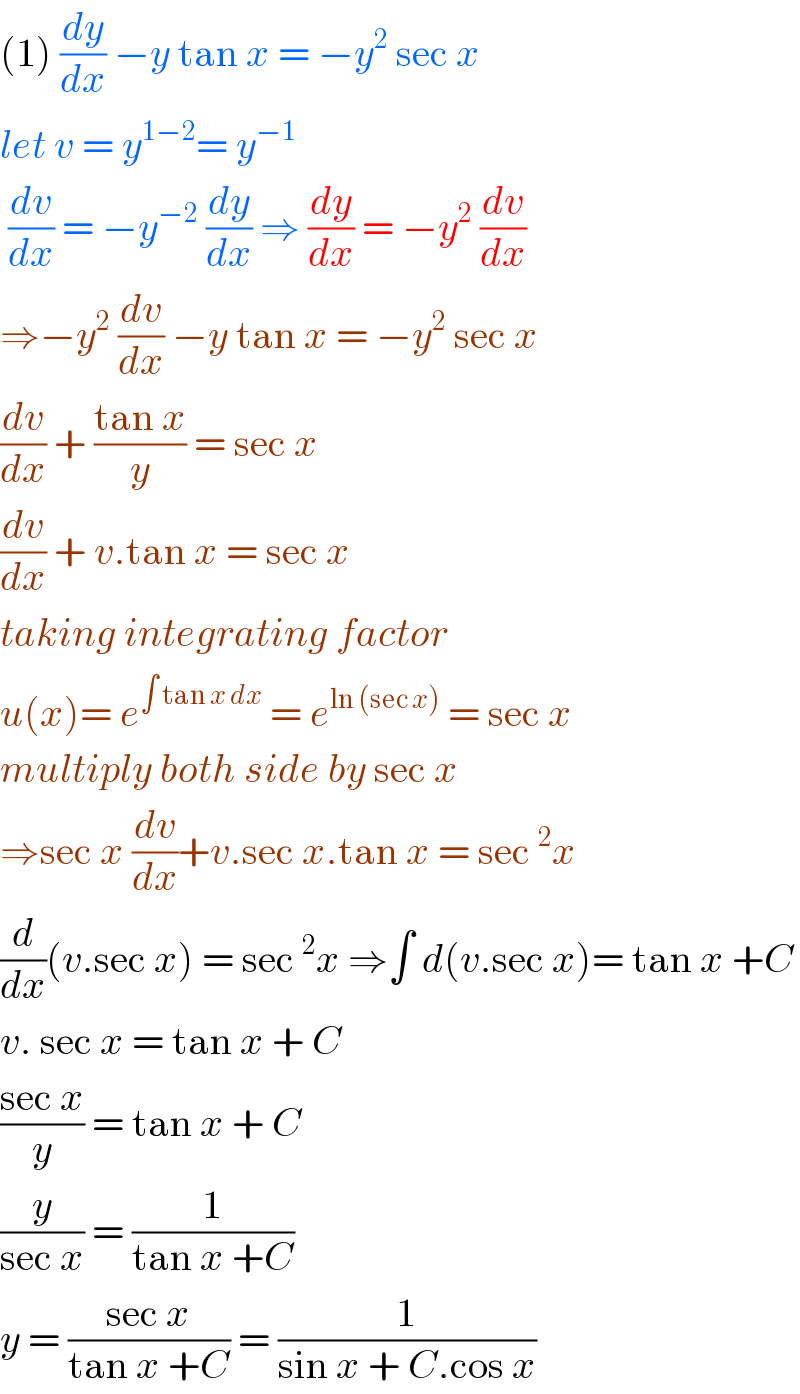
$$\left(\mathrm{1}\right)\:\frac{{dy}}{{dx}}\:−{y}\:\mathrm{tan}\:{x}\:=\:−{y}^{\mathrm{2}} \:\mathrm{sec}\:{x} \\ $$$${let}\:{v}\:=\:{y}^{\mathrm{1}−\mathrm{2}} =\:{y}^{−\mathrm{1}} \\ $$$$\:\frac{{dv}}{{dx}}\:=\:−{y}^{−\mathrm{2}} \:\frac{{dy}}{{dx}}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:−{y}^{\mathrm{2}} \:\frac{{dv}}{{dx}} \\ $$$$\Rightarrow−{y}^{\mathrm{2}} \:\frac{{dv}}{{dx}}\:−{y}\:\mathrm{tan}\:{x}\:=\:−{y}^{\mathrm{2}} \:\mathrm{sec}\:{x}\: \\ $$$$\frac{{dv}}{{dx}}\:+\:\frac{\mathrm{tan}\:{x}}{{y}}\:=\:\mathrm{sec}\:{x}\: \\ $$$$\frac{{dv}}{{dx}}\:+\:{v}.\mathrm{tan}\:{x}\:=\:\mathrm{sec}\:{x} \\ $$$${taking}\:{integrating}\:{factor} \\ $$$${u}\left({x}\right)=\:{e}^{\int\:\mathrm{tan}\:{x}\:{dx}} \:=\:{e}^{\mathrm{ln}\:\left(\mathrm{sec}\:{x}\right)} \:=\:\mathrm{sec}\:{x} \\ $$$${multiply}\:{both}\:{side}\:{by}\:\mathrm{sec}\:{x} \\ $$$$\Rightarrow\mathrm{sec}\:{x}\:\frac{{dv}}{{dx}}+{v}.\mathrm{sec}\:{x}.\mathrm{tan}\:{x}\:=\:\mathrm{sec}\:^{\mathrm{2}} {x}\: \\ $$$$\frac{{d}}{{dx}}\left({v}.\mathrm{sec}\:{x}\right)\:=\:\mathrm{sec}\:^{\mathrm{2}} {x}\:\Rightarrow\int\:{d}\left({v}.\mathrm{sec}\:{x}\right)=\:\mathrm{tan}\:{x}\:+{C} \\ $$$${v}.\:\mathrm{sec}\:{x}\:=\:\mathrm{tan}\:{x}\:+\:{C}\: \\ $$$$\frac{\mathrm{sec}\:{x}}{{y}}\:=\:\mathrm{tan}\:{x}\:+\:{C}\: \\ $$$$\frac{{y}}{\mathrm{sec}\:{x}}\:=\:\frac{\mathrm{1}}{\mathrm{tan}\:{x}\:+{C}}\: \\ $$$${y}\:=\:\frac{\mathrm{sec}\:{x}}{\mathrm{tan}\:{x}\:+{C}}\:=\:\frac{\mathrm{1}}{\mathrm{sin}\:{x}\:+\:{C}.\mathrm{cos}\:{x}} \\ $$
Commented by bobhans last updated on 12/Aug/20
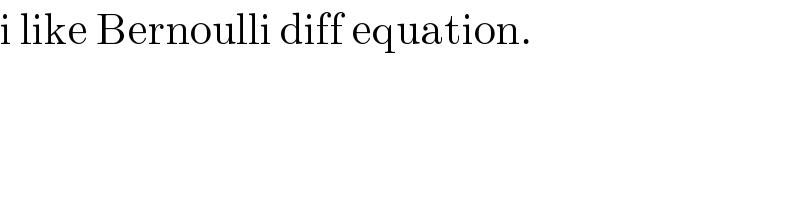
$$\mathrm{i}\:\mathrm{like}\:\mathrm{Bernoulli}\:\mathrm{diff}\:\mathrm{equation}. \\ $$
Commented by john santu last updated on 12/Aug/20

$${Bernoulli}….{great}…..{and}\:{cooll} \\ $$
Answered by Ar Brandon last updated on 12/Aug/20
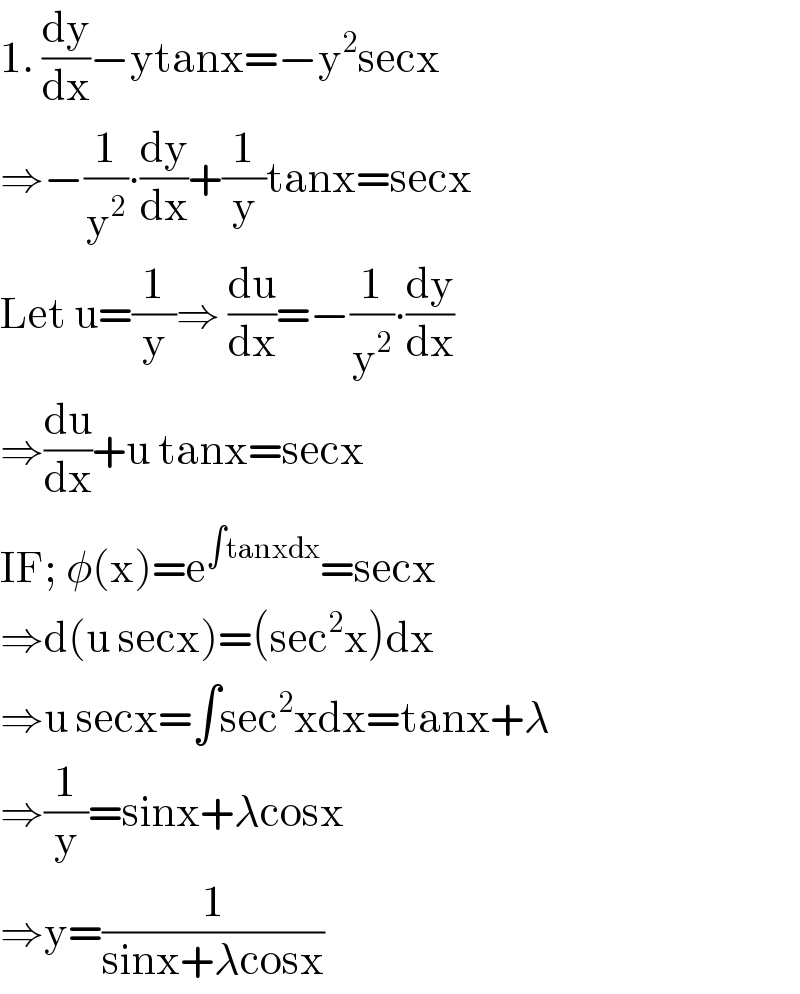
$$\mathrm{1}.\:\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{ytanx}=−\mathrm{y}^{\mathrm{2}} \mathrm{secx} \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} }\centerdot\frac{\mathrm{dy}}{\mathrm{dx}}+\frac{\mathrm{1}}{\mathrm{y}}\mathrm{tanx}=\mathrm{secx} \\ $$$$\mathrm{Let}\:\mathrm{u}=\frac{\mathrm{1}}{\mathrm{y}}\Rightarrow\:\frac{\mathrm{du}}{\mathrm{dx}}=−\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} }\centerdot\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$$$\Rightarrow\frac{\mathrm{du}}{\mathrm{dx}}+\mathrm{u}\:\mathrm{tanx}=\mathrm{secx} \\ $$$$\mathrm{IF};\:\phi\left(\mathrm{x}\right)=\mathrm{e}^{\int\mathrm{tanxdx}} =\mathrm{secx} \\ $$$$\Rightarrow\mathrm{d}\left(\mathrm{u}\:\mathrm{secx}\right)=\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx} \\ $$$$\Rightarrow\mathrm{u}\:\mathrm{secx}=\int\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}=\mathrm{tanx}+\lambda \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{y}}=\mathrm{sinx}+\lambda\mathrm{cosx}\: \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{1}}{\mathrm{sinx}+\lambda\mathrm{cosx}} \\ $$
Answered by Ar Brandon last updated on 12/Aug/20
![2. Π_(k=1) ^(25) (x+(x/3^k ))=1⇒x^(25) Π_(k=1) ^(25) (1+(1/3^k ))=1 ⇒x=[Π_(k=1) ^(25) (1+(1/3^k ))]^(−(1/(25)) ) =Π_(k=1) ^(25) [1+(1/3^k )]^(−(1/(25)))](https://www.tinkutara.com/question/Q107848.png)
$$\mathrm{2}.\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{25}} {\prod}}\left(\mathrm{x}+\frac{\mathrm{x}}{\mathrm{3}^{\mathrm{k}} }\right)=\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{25}} \underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{25}} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{k}} }\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\left[\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{25}} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{k}} }\right)\right]^{−\frac{\mathrm{1}}{\mathrm{25}}\:} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{25}} {\prod}}\left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{k}} }\right]^{−\frac{\mathrm{1}}{\mathrm{25}}} \\ $$
