Question Number 32939 by abdo imad last updated on 06/Apr/18
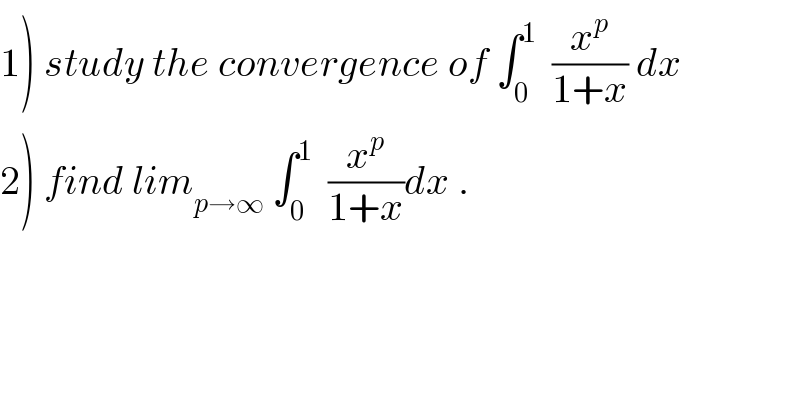
$$\left.\mathrm{1}\right)\:{study}\:{the}\:{convergence}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{{p}} }{\mathrm{1}+{x}}\:{dx} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{p}\rightarrow\infty} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{{p}} }{\mathrm{1}+{x}}{dx}\:. \\ $$
Commented by abdo imad last updated on 08/Apr/18
![let put I =∫_0 ^1 (x^p /(1+x))dx .ch.x=(1/t) give I = ∫_1 ^(+∞) (1/(t^p (1+(1/t)))) (dt/t^2 ) = ∫_1 ^(+∞) (dt/(t^(p+2) +t^(p+1) )) = ∫_1 ^(+∞) (dt/(t^(p+2) ( 1+(1/t)))) .and at V(∞) (1/(t^(p+2) (1+(1/t))))∼ (1/t^(p+2) ) ∫_1 ^(+∞) (dt/t^(p+2) ) converges ⇔ p+2>1 ⇔p >−1 .so I converges ⇔ p>−1 . 2) ∀ x∈[0,1] (x^p /(1+x)) ≤ x^p ⇒ ∫_0 ^1 (x^p /(1+x)) dx ≤ ∫_0 ^1 x^p dx=(1/(p+1)) ⇒ lim_(p→∞) ∫_0 ^1 (x^p /(1+x)) dx =0 .](https://www.tinkutara.com/question/Q32967.png)
$${let}\:{put}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{{p}} }{\mathrm{1}+{x}}{dx}\:.{ch}.{x}=\frac{\mathrm{1}}{{t}}\:{give} \\ $$$${I}\:=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\:\frac{\mathrm{1}}{{t}^{{p}} \left(\mathrm{1}+\frac{\mathrm{1}}{{t}}\right)}\:\frac{{dt}}{{t}^{\mathrm{2}} }\:=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\frac{{dt}}{{t}^{{p}+\mathrm{2}} \:+{t}^{{p}+\mathrm{1}} } \\ $$$$=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\frac{{dt}}{{t}^{{p}+\mathrm{2}} \left(\:\mathrm{1}+\frac{\mathrm{1}}{{t}}\right)}\:\:.{and}\:{at}\:{V}\left(\infty\right)\:\:\frac{\mathrm{1}}{{t}^{{p}+\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{t}}\right)}\sim\:\:\frac{\mathrm{1}}{{t}^{{p}+\mathrm{2}} } \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dt}}{{t}^{{p}+\mathrm{2}} }\:{converges}\:\Leftrightarrow\:{p}+\mathrm{2}>\mathrm{1}\:\Leftrightarrow{p}\:>−\mathrm{1}\:.{so} \\ $$$${I}\:{converges}\:\Leftrightarrow\:{p}>−\mathrm{1}\:. \\ $$$$\left.\mathrm{2}\right)\:\forall\:{x}\in\left[\mathrm{0},\mathrm{1}\right]\:\:\frac{{x}^{{p}} }{\mathrm{1}+{x}}\:\leqslant\:{x}^{{p}} \:\Rightarrow\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{{p}} }{\mathrm{1}+{x}}\:{dx}\:\leqslant\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{p}} {dx}=\frac{\mathrm{1}}{{p}+\mathrm{1}}\:\Rightarrow \\ $$$${lim}_{{p}\rightarrow\infty} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{{p}} }{\mathrm{1}+{x}}\:{dx}\:=\mathrm{0}\:. \\ $$
Answered by JDamian last updated on 08/Apr/18
![1) (x^p /(1+x))=x^(p−1) −x^(p−2) + ∙∙∙ (−1)^(p+1) +(((−1)^p )/(x+1))=Σ_(k=0) ^(p−1) (−1)^(p+k+1) x^k ∫_0 ^1 (x^p /(1+x))=[(x^p /p)−(x^(p−1) /(p−1))+ ∙∙∙ +(−1)^(p+1) +(−1)^p ln∣x+1∣]_0 ^1 = =[Σ_(k=1) ^p (−1)^(p+k) (x^k /k) + (−1)^p ln∣x+1∣]_0 ^1 =Σ_(k=1) ^p (((−1)^(p+k) )/k) + (−1)^p ln2= =(1/p)−(1/(p−1))+ ∙∙∙ +(−1)^(p+1) + (−1)^p ln2](https://www.tinkutara.com/question/Q32964.png)
$$ \\ $$$$\left.\mathrm{1}\right)\:\frac{{x}^{{p}} }{\mathrm{1}+{x}}={x}^{{p}−\mathrm{1}} −{x}^{{p}−\mathrm{2}} +\:\centerdot\centerdot\centerdot\:\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} +\frac{\left(−\mathrm{1}\right)^{{p}} }{{x}+\mathrm{1}}=\underset{{k}=\mathrm{0}} {\overset{{p}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{p}+{k}+\mathrm{1}} {x}^{{k}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{p}} }{\mathrm{1}+{x}}=\left[\frac{{x}^{{p}} }{{p}}−\frac{{x}^{{p}−\mathrm{1}} }{{p}−\mathrm{1}}+\:\centerdot\centerdot\centerdot\:+\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} +\left(−\mathrm{1}\right)^{{p}} {ln}\mid{x}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$=\left[\underset{{k}=\mathrm{1}} {\overset{{p}} {\sum}}\left(−\mathrm{1}\right)^{{p}+{k}} \:\frac{{x}^{{k}} }{{k}}\:\:+\:\:\left(−\mathrm{1}\right)^{{p}} {ln}\mid{x}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{p}} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{p}+{k}} \:}{{k}}\:\:+\:\:\left(−\mathrm{1}\right)^{{p}} {ln}\mathrm{2}= \\ $$$$=\frac{\mathrm{1}}{{p}}−\frac{\mathrm{1}}{{p}−\mathrm{1}}+\:\centerdot\centerdot\centerdot\:+\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} \:\:+\:\:\left(−\mathrm{1}\right)^{{p}} {ln}\mathrm{2} \\ $$
