Question Number 20574 by khamizan833@gmail.com last updated on 28/Aug/17
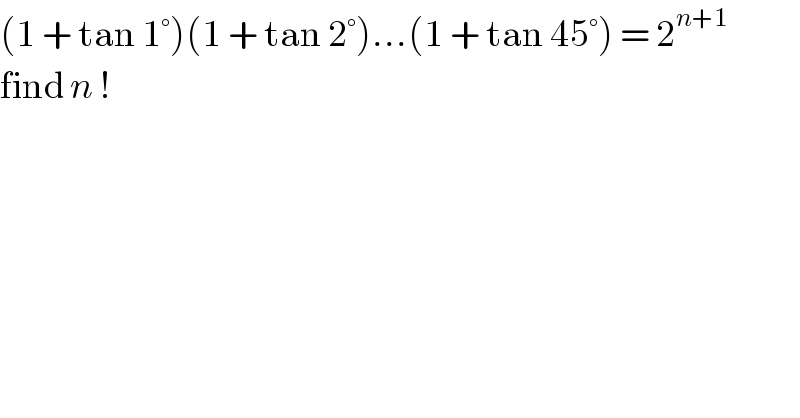
$$\left(\mathrm{1}\:+\:\mathrm{tan}\:\mathrm{1}°\right)\left(\mathrm{1}\:+\:\mathrm{tan}\:\mathrm{2}°\right)…\left(\mathrm{1}\:+\:\mathrm{tan}\:\mathrm{45}°\right)\:=\:\mathrm{2}^{{n}+\mathrm{1}} \\ $$$$\mathrm{find}\:{n}\:! \\ $$
Answered by Tinkutara last updated on 28/Aug/17

$$\left(\mathrm{1}+\mathrm{tan}\:\mathrm{1}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{44}°\right)=\mathrm{1}+\mathrm{tan}\:\mathrm{44}°+ \\ $$$$\mathrm{tan}\:\mathrm{1}°+\mathrm{tan}\:\mathrm{1}°\mathrm{tan}\:\mathrm{44}° \\ $$$$\mathrm{tan}\:\mathrm{45}°=\frac{\mathrm{tan}\:\mathrm{1}°+\mathrm{tan}\:\mathrm{44}°}{\mathrm{1}−\mathrm{tan}\:\mathrm{1}°\mathrm{tan}\:\mathrm{44}°}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{1}°+\mathrm{tan}\:\mathrm{44}°+\mathrm{tan}\:\mathrm{1}°\mathrm{tan}\:\mathrm{44}°=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{tan}\:\mathrm{1}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{44}°\right)=\mathrm{2} \\ $$$$\mathrm{1}+\mathrm{tan}\:\mathrm{45}°=\mathrm{2} \\ $$$$\left(\mathrm{1}\:+\:\mathrm{tan}\:\mathrm{1}°\right)\left(\mathrm{1}\:+\:\mathrm{tan}\:\mathrm{2}°\right)…\left(\mathrm{1}\:+\:\mathrm{tan}\:\mathrm{45}°\right) \\ $$$$=\mathrm{2}^{\mathrm{22}} ×\mathrm{2}=\mathrm{2}^{\mathrm{23}} \\ $$
