Question Number 113656 by bobhans last updated on 14/Sep/20
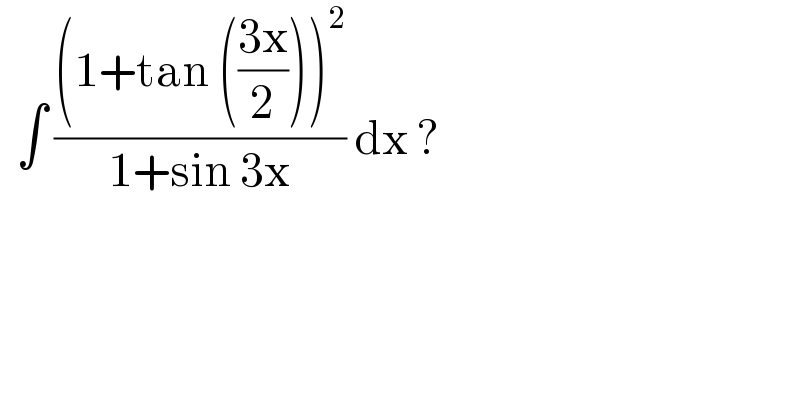
$$\:\:\int\:\frac{\left(\mathrm{1}+\mathrm{tan}\:\left(\frac{\mathrm{3x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{sin}\:\mathrm{3x}}\:\mathrm{dx}\:? \\ $$
Answered by john santu last updated on 14/Sep/20
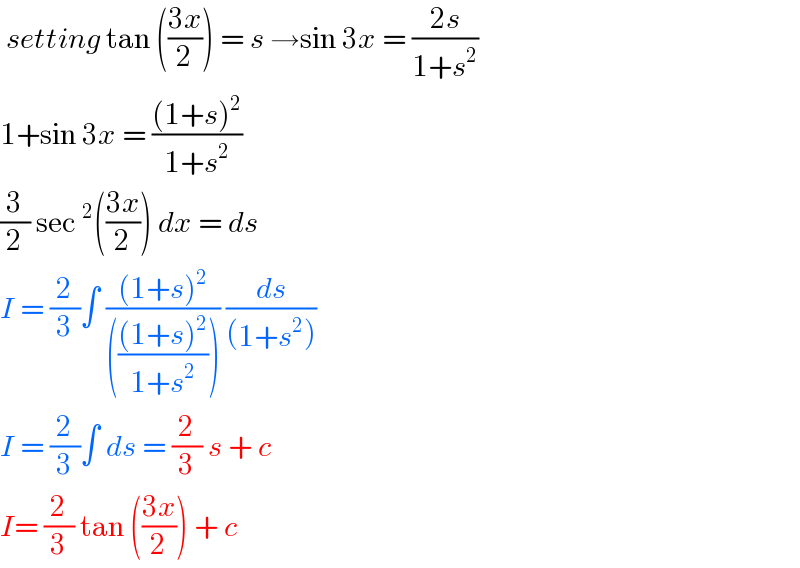
$$\:{setting}\:\mathrm{tan}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\:=\:{s}\:\rightarrow\mathrm{sin}\:\mathrm{3}{x}\:=\:\frac{\mathrm{2}{s}}{\mathrm{1}+{s}^{\mathrm{2}} } \\ $$$$\mathrm{1}+\mathrm{sin}\:\mathrm{3}{x}\:=\:\frac{\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }{\mathrm{1}+{s}^{\mathrm{2}} }\: \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{sec}\:^{\mathrm{2}} \left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\:{dx}\:=\:{ds}\: \\ $$$${I}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }{\left(\frac{\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }{\mathrm{1}+{s}^{\mathrm{2}} }\right)}\:\frac{{ds}}{\left(\mathrm{1}+{s}^{\mathrm{2}} \right)} \\ $$$${I}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\int\:{ds}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:{s}\:+\:{c}\: \\ $$$${I}=\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{tan}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\:+\:{c}\: \\ $$
