Question Number 163099 by HongKing last updated on 03/Jan/22
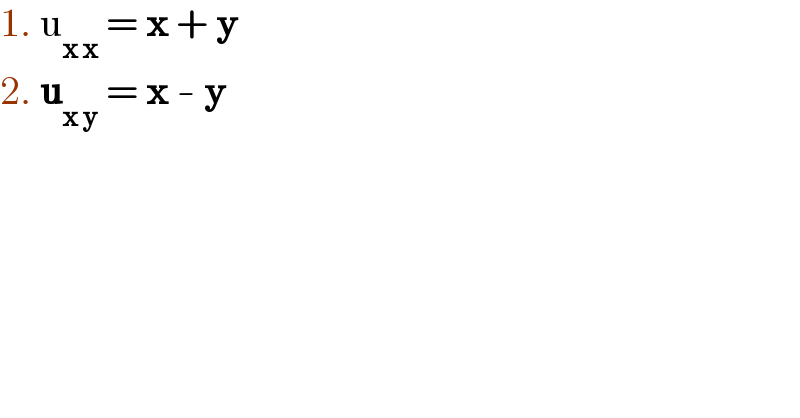
$$\mathrm{1}.\:\mathrm{u}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{x}}} \:=\:\boldsymbol{\mathrm{x}}\:+\:\boldsymbol{\mathrm{y}} \\ $$$$\mathrm{2}.\:\boldsymbol{\mathrm{u}}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{y}}} \:=\:\boldsymbol{\mathrm{x}}\:-\:\boldsymbol{\mathrm{y}} \\ $$
Answered by mr W last updated on 04/Jan/22
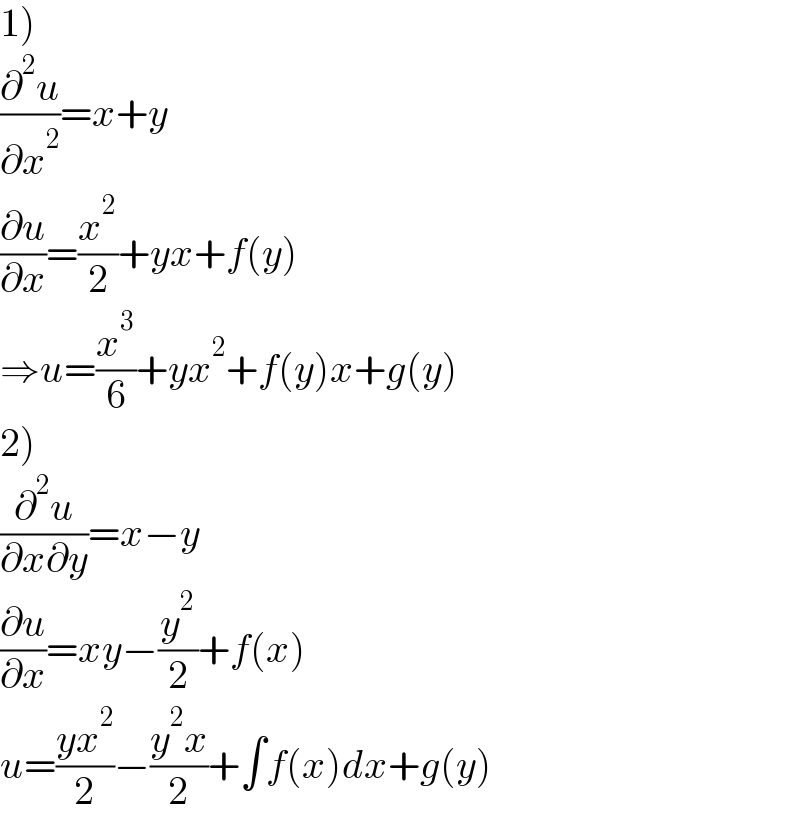
$$\left.\mathrm{1}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {u}}{\partial{x}^{\mathrm{2}} }={x}+{y} \\ $$$$\frac{\partial{u}}{\partial{x}}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{yx}+{f}\left({y}\right) \\ $$$$\Rightarrow{u}=\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{yx}^{\mathrm{2}} +{f}\left({y}\right){x}+{g}\left({y}\right) \\ $$$$\left.\mathrm{2}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {u}}{\partial{x}\partial{y}}={x}−{y} \\ $$$$\frac{\partial{u}}{\partial{x}}={xy}−\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+{f}\left({x}\right) \\ $$$${u}=\frac{{yx}^{\mathrm{2}} }{\mathrm{2}}−\frac{{y}^{\mathrm{2}} {x}}{\mathrm{2}}+\int{f}\left({x}\right){dx}+{g}\left({y}\right) \\ $$
Commented by HongKing last updated on 05/Jan/22
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
