Question Number 43991 by Tawa1 last updated on 19/Sep/18

$$\int\:\frac{\mathrm{1}}{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\:\:\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\:\:\mathrm{dx} \\ $$
Answered by Joel578 last updated on 19/Sep/18
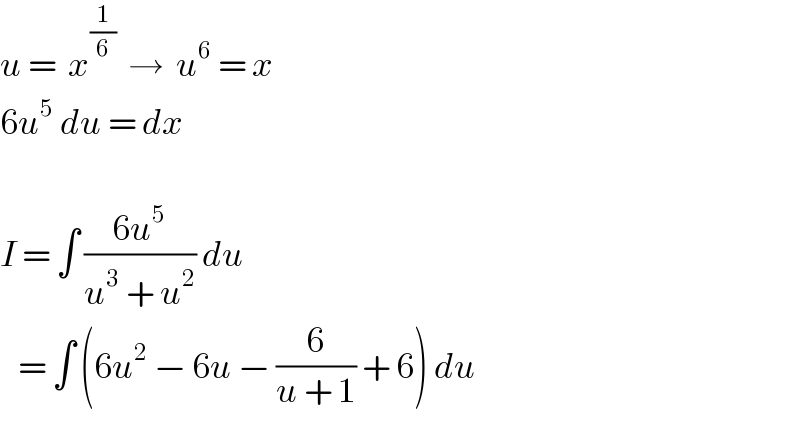
$${u}\:=\:\:{x}^{\frac{\mathrm{1}}{\mathrm{6}}} \:\:\rightarrow\:\:{u}^{\mathrm{6}} \:=\:{x} \\ $$$$\mathrm{6}{u}^{\mathrm{5}} \:{du}\:=\:{dx} \\ $$$$ \\ $$$${I}\:=\:\int\:\frac{\mathrm{6}{u}^{\mathrm{5}} }{{u}^{\mathrm{3}} \:+\:{u}^{\mathrm{2}} }\:{du} \\ $$$$\:\:\:=\:\int\:\left(\mathrm{6}{u}^{\mathrm{2}} \:−\:\mathrm{6}{u}\:−\:\frac{\mathrm{6}}{{u}\:+\:\mathrm{1}}\:+\:\mathrm{6}\right)\:{du} \\ $$
Answered by MJS last updated on 19/Sep/18
![∫(dx/(x^(1/2) +x^(1/3) ))=∫(dx/(x^(2/6) (x^(1/6) +1)))= [t=x^(1/6) → dx=6x^(5/6) dt] =6∫(t^3 /((t+1)))dt= [u=t+1 → du=dt] =6∫(((u−1)^3 )/u)du=6∫(u^2 −3u+3−(1/u))du= =6((u^3 /3)−((3u^2 )/2)+3u−ln u)=2u^3 −9u^2 +18u−6ln u= =2(t+1)^3 −9(t+1)^2 +18(t+1)−6ln(t+1)= =2t^3 −3t^2 +6t+11−6ln(t+1)= =2x^(1/2) −3x^(1/3) +6x^(1/6) +11−6ln(x^(1/6) +1)= [11 as a constant merges in C] =2x^(1/2) −3x^(1/3) +6x^(1/6) −6ln(x^(1/6) +1)+C](https://www.tinkutara.com/question/Q43997.png)
$$\int\frac{{dx}}{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +{x}^{\frac{\mathrm{1}}{\mathrm{3}}} }=\int\frac{{dx}}{{x}^{\frac{\mathrm{2}}{\mathrm{6}}} \left({x}^{\frac{\mathrm{1}}{\mathrm{6}}} +\mathrm{1}\right)}= \\ $$$$\:\:\:\:\:\left[{t}={x}^{\frac{\mathrm{1}}{\mathrm{6}}} \:\rightarrow\:{dx}=\mathrm{6}{x}^{\frac{\mathrm{5}}{\mathrm{6}}} {dt}\right] \\ $$$$=\mathrm{6}\int\frac{{t}^{\mathrm{3}} }{\left({t}+\mathrm{1}\right)}{dt}= \\ $$$$\:\:\:\:\:\left[{u}={t}+\mathrm{1}\:\rightarrow\:{du}={dt}\right] \\ $$$$=\mathrm{6}\int\frac{\left({u}−\mathrm{1}\right)^{\mathrm{3}} }{{u}}{du}=\mathrm{6}\int\left({u}^{\mathrm{2}} −\mathrm{3}{u}+\mathrm{3}−\frac{\mathrm{1}}{{u}}\right){du}= \\ $$$$=\mathrm{6}\left(\frac{{u}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{3}{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{3}{u}−\mathrm{ln}\:{u}\right)=\mathrm{2}{u}^{\mathrm{3}} −\mathrm{9}{u}^{\mathrm{2}} +\mathrm{18}{u}−\mathrm{6ln}\:{u}= \\ $$$$=\mathrm{2}\left({t}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{9}\left({t}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{18}\left({t}+\mathrm{1}\right)−\mathrm{6ln}\left({t}+\mathrm{1}\right)= \\ $$$$=\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{6}{t}+\mathrm{11}−\mathrm{6ln}\left({t}+\mathrm{1}\right)= \\ $$$$=\mathrm{2}{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{3}{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{6}{x}^{\frac{\mathrm{1}}{\mathrm{6}}} +\mathrm{11}−\mathrm{6ln}\left({x}^{\frac{\mathrm{1}}{\mathrm{6}}} +\mathrm{1}\right)= \\ $$$$\:\:\:\:\:\left[\mathrm{11}\:\mathrm{as}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{merges}\:\mathrm{in}\:{C}\right] \\ $$$$=\mathrm{2}{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{3}{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{6}{x}^{\frac{\mathrm{1}}{\mathrm{6}}} −\mathrm{6ln}\left({x}^{\frac{\mathrm{1}}{\mathrm{6}}} +\mathrm{1}\right)+{C} \\ $$
